波形套軸向受壓仿真與參數優化研究*
徐行勝,周 旭,伍 英
(湖北汽車工業學院 機械工程學院,湖北 十堰 442002)
0 引 言
波形套是汽車驅動橋主動錐齒輪總成上的重要零件,由于中間波形區的特殊結構,它可將驅動橋主動錐齒輪軸承預緊力調至最佳狀態,并且可以防止預緊力過大,提高傳動效率和裝配效率,降低主減速器總成噪音,提高軸承使用壽命。波形套中間波形區可使波形套在一定軸向變形內軸向力的大小基本保持不變,因此,波形套被廣泛應用于軸承的預緊[1-2]。
當前,已有多位學者對波形套進行了不同領域的研究。文獻[3]對驅動橋主動錐齒輪軸承的預緊參數進行了計算和分析,對波形套達到屈服極限時所需壓力進行了分析研究;文獻[4]分析了主動錐齒輪總成裝配力,但僅對波形套進行了定性分析;文獻[5]利用有限元分析軟件Abaqus分析了考慮塑性加工和不考慮塑性加工的波形套壓力與應變的關系,得出了考慮塑性加工的波形套與試驗更接近的結果;文獻[6]利用有限元方法對主減總成進行了分析,對波形套的載荷和回彈量進行了設計,并評估了波形套對軸承的支持剛度;文獻[7]用有限元仿真分析法對波形套進行了數值模擬,揭示了塑性加工對波形套的軸向受壓過程軸向力的影響;文獻[8-11]對波形套的復合縮徑-脹形變形進行了試驗研究,對波形套進行了成形特點分析和應力場求解,初步研究了波形套結構參數對軸向力的影響;文獻[12-13]用數值模擬的方法分析了帶有錐面的波形套幾何參數對波形套軸向受壓過程中軸向力的影響,并利用第二代非劣遺傳算法,對隔套的軸向性能進行了多目標優化。
但目前對于常見的中間為3段圓弧波形套的優化設計未見相關文獻報道。對此,本文將利用有限元法對應用廣泛的常見波形套進行仿真[14-15],并建立正交試驗組,構造波形套在受壓過程中從0.98倍~1倍的最大軸向力對應的工作段長度的二階響應面模型,并利用遺傳算法進行優化,使最佳工作段長度最大。
1 波形套的結構參數
波形套的結構有多種形式,根據實際工程中的應用,本文對常見的波形套作優化研究,利用Abaqus軟件對其進行軸向壓縮的有限元數值模擬仿真。
波形套的結構如圖1所示。

圖1 波形套的結構t—壁厚;R1—上端過渡圓弧半徑;R2—中間凸起波形圓弧半徑;R3—下端過渡圓弧半徑;B—中間凸起波形徑向高度;D1—小端直徑;D2—大端直徑;H—軸向總高度;HB—中間波形區軸向高度
圖1的波形套結構中,上、下兩端為直壁部分,中部為波形區,由3段圓弧組成;中間凸起部分圓弧與上、下兩直壁分別通過一段圓弧過渡。
2 波形套有限元仿真分析
2.1 波形套仿真參數
波形套的材料為20號優質碳素結構鋼,它具有良好的塑性性能,作為有限元仿真的材料屬性輸入;彈性模量E=196.5 GPa,泊松比為μ=0.29。
20鋼真實應力應變如表1所示。
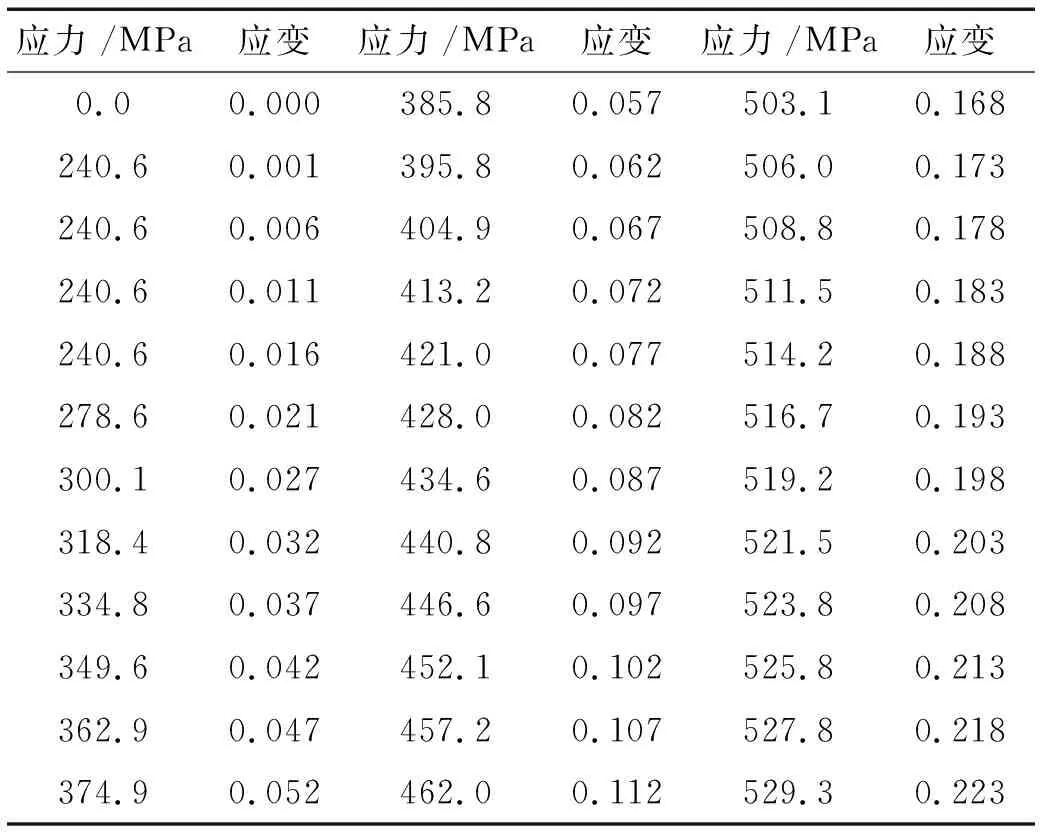
表1 20鋼真實應力應變
波形套的幾何參數為:
D1=69 mm,D2=73 mm,H=79 mm,HB=30 mm,t=3 mm,R1=12 mm,R2=18 mm,R3=12 mm,B=6 mm。
2.2 波形套仿真過程及結果分析
筆者利用有限元法對波形套進行數值模擬仿真,仿真采用四節點軸對稱單元模型。
波形套的有限元模型如圖2所示。
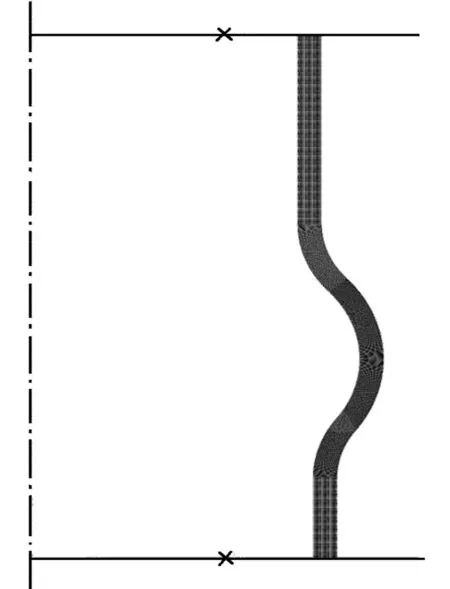
圖2 波形套的有限元模型
圖2的波形套有限元模型中,上、下兩端為軸對稱解析剛體,使上端剛體向下壓縮5 mm;網格劃分時將截面分割成若干個矩形與扇區,可使截面網格劃分的比較規則;整個仿真過程中,始終打開幾何非線性選項。
在有限元仿真過程中,根據所設置的分析步,Abaqus軟件可計算得到多組軸向力與壓縮位移的關系點,將所得到的數據點導入到Matlab畫圖。
可得到波形套的軸向力壓縮量曲線,如圖3所示。
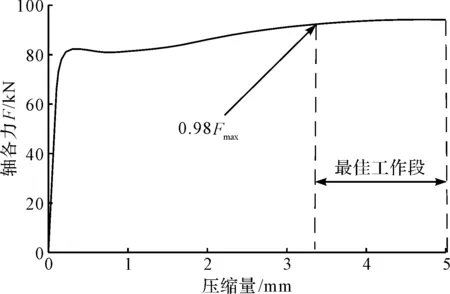
圖3 波形套的軸向力壓縮量曲線
圖3中,軸向力大小先隨壓縮位移的增大而增大,接著材料進入了屈服階段;隨著壓縮量的增加,軸向力基本保持不變,仿真結果與材料力學中塑性材料的壓縮特性曲線相一致。
在設計波形套時,應優先采用低碳鋼等屈服強度合適的材料。筆者根據Abaqus計算所得到的軸向力與壓縮量關系點,在實際工程應用中,可以取軸向力值在[0.98Fmax,Fmax]區間為工作段,此時波形套在該區間對應的軸向位移段具有較好的工作性能。如在軸承預緊中,當波形套在工作中受到磨損后仍有一定的軸向力,以保證軸承有一定的預緊力,從而增加軸承的使用壽命。
同時,在進行優化設計時,可將該工作段對應的軸向位移長度定為優化設計目標。
3 優化設計
3.1 正交試驗組的建立
正交試驗設計是用于多因素試驗的一種方法。利用正交試驗點具有均勻整齊的特點,可從全面試驗中挑選出部分具有代表性的試驗點進行試驗,以減小波形套的仿真次數。
波形套的設計參數有5個,每個參數取4個水平。為了保證試驗的精度與充分,采用L64(421)正交表,任取其中5列作為試驗設計表,一共64組試驗。
每個水平下,各參數因子水平如表2所示。
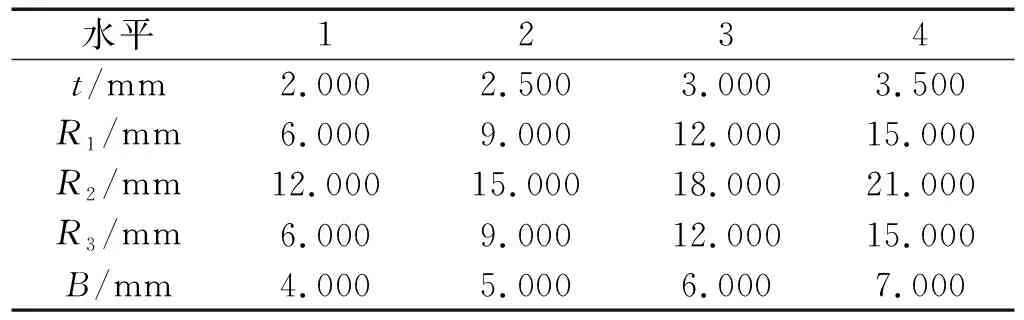
表2 各參數因子水平
3.2 二階響應面模型的構造
采用響應面法來近似代替有限元法分析,則可大幅度地減少波形套有限元仿真計算的時間,減小波形套設計的周期。筆者先構造二階響應面模型,再利用各種成熟的優化算法來優化響應,得到優化后的波形套的幾何參數。
二階響應面模型如下:
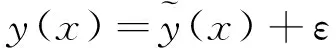
(1)
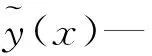
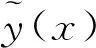
(2)
二階響應面近似函數的二階多項式中共有5個因素,至少需要21組樣本點才能解出每個系數。正交試驗得出了64組試驗樣本點,根據最小二乘法原理利用Matlab軟件,可以擬合出0.98倍~1倍的最大軸向力對應的變形工作段軸向位移長度的二階響應面,擬合得出的近似函數的各系數的值為:βi=[-1.741 5,-0.031 2,0.322 0,-0.012 1,-0.377 5],βij=[0.000 6,0.031 7,0.010 0,-0.030 3,0.000 9,0.001 6,-0.002 2,-0.001 2,0.002 5,0.000 9],β0=4.082 2,β5+i=[0.093 6,0.000 3,-0.011 8,-0.000 5,0.027 9]。
擬合精度R2=0.969 6,響應與樣本非常接近,能夠較好地代替有限元,為波形套幾何參數的優化做準備。
3.3 遺傳算法
遺傳算法的本質是一種建立在遺傳學和自然選擇原理基礎上的一種自適應的全局優化和搜索方法[16]。二階響應面為非線性模型,利用遺傳算法能夠較好地求解一些非線性函數的優化問題。
筆者以波形套的最佳軸向變形工作段對應的軸向位移長度最大為優化設計目標,結構參數為設計變量。由于波形套波形區內側受壓應力,外側受拉應力,經過多次仿真;考慮到波形套可能因塑性屈服而發生破壞,在最大軸向力的選取時,考慮到強度等要求,通過Matlab遺傳算法工具箱,則可以快速地對目標函數進行求解。
設置波形套的設計變量取值范圍,如表3所示。

表3 設計變量的取值范圍
4 優化結果及分析
筆者利用遺傳算法對波形套結構參數進行優化,優化結果如表4所示。

表4 優化結果
筆者將優化后的結果代入到Abaqus軟件進行計算,將用有限元法計算出的結果與響應面法計算出的結果進行對比。
有限元與響應面對比如表5所示。

表5 有限元與響應面對比
從表5可以看出:用響應面模型近似得到的0.98倍~1倍最大軸向力對應的變形工作段軸向位移長度的結果,與有限元計算得到的結果相對誤差為0.31%,說明響應面模型代替有限元模型具有較高的精度,優化求得的波形套幾何參數是可靠的。
5 結束語
本研究通過Abaqus有限元軟件,對波形套進行了軸向受壓仿真研究,分析了軸向力隨壓縮量的曲線變化規律;利用正交試驗得到了樣本數據,構造了波形套在軸向受壓過程中,從0.98倍~1倍的最大軸向力對應的變形工作段軸向位移長度的二階響應面模型,采用遺傳算法對響應進行了優化。
研究結果表明:優化后的響應與有限元計算結果相對誤差為0.31%,響應可近似代替有限元法分析;通過這一方法,使最佳變形工作段的軸向位移長度最大,為實際工程中波形套的參數設計提供了參考。
在研究過程中,由于考慮到波形套的最大軸向力和強度等要求,所設計的變量范圍較小,只以波形套的最佳軸向變形工作段軸向位移為優化目標,未將塑性應變作為優化目標。
在后續工作中,可將塑性應變一起作多目標的優化設計。同時,隨著波形套結構的多樣化,對不同結構形式的波形套仍需進行研究。
參考文獻(References):
[1] QI Y M, ZHU X Z, DENG S P. et al. Research on spindle bearing pre-tightening based on spacer sleeve adjustment[J]. Applied Mechanics and Materials, 2014(488-489):1087-1090.
[2] 許 志,洪暾暉.可壓縮隔套對主齒總成竄動的影響[J].機械工程師,2012(3):128-129.
[3] 唐自玉,邴麗榮.后橋主齒軸承預緊力的力學分析及可壓縮隔套的設計[J].汽車技術,2001(10):18-20.
[4] 曹 張.汽車后橋主減速器裝配過程的力學性能分析與隔套選型[D].合肥:合肥工業大學工程力學系,2006.
[5] 余顯忠,黃平輝,揭 鋼.彈性隔套設計與仿真分析[J].現代制造工程,2010(3):1-4.
[6] 馮 立,謝玉琳,蔡卓琳,等.有限元分析在彈性隔套設計中的應用[J].時代汽車,2018(4):89-91.
[7] LIU Y, MONKABA V D. Forming simulation and stiffness prediction of a rear axle pinion bearing collapsible spacer[C].International Truck and Bus Meeting ang Exhibition ,Chicago:SAE,2001.
[8] 王連東,劉 敏,張啟中.波形套的試驗研究[J].中國機械工程,2004(24):12-14.
[9] 彭加耕,王連東,梁 辰,等.波形套復合縮徑-脹形變形分析及應力場求解[J].塑性工程學報,2002,9(2):72-75.
[10] 王連東,邱蘭芳,劉 敏.波形套工作特性的理論與試驗研究[J].機械工程學報,2005,41(11):188-192.
[11] 王連東,彭加耕,劉助柏,等.汽車波形套復合縮徑-脹形變形分析與求解[J].機械工程學報,2002,38(5):149-152.
[12] 桂良進,朱升發,陳偉博,等.波形套的軸向受壓分析與優化設計[J].清華大學學報:自然科學版,2019,59(3):219-227.
[13] 陳偉博.驅動橋主錐總成可壓縮隔套的設計與開發[D].北京:清華大學汽車工程系,2017.
[14] 魏延剛,宋宇謨,劉彥奎.基于有限元法的推力圓錐滾子軸承動態接觸分析[J].機電工程,2019,36(4):352-356.
[15] 曾祥錄,韓俊峰,朱留憲,等.菌形葉根型線銑刀的三維建模及有限元分析研究[J].機電工程,2019,36(3):284-288.
[16] VERMA V K, KUMAR B. Genetic algorithm: an overview and its application[J]. International Journal of Advanced Studies in Computer Science and Engineering, 2014,3(2):21-27.

