基于驅控一體的伺服壓力機控制系統研究*

汪宇其，李澤源，李向國，朱燈林，梅志千

(1.河海大學 機電工程學院，江蘇 常州 213022；2.固高科技運動控制研究院，廣東 深圳 518057)

0 引 言

自上世紀90年代以來，隨著沖壓行業對加工裝備的智能化和柔性化要求逐漸提高，伺服壓力機應運而生，并廣泛應用于沖壓、落料及鈑金成型等領域。相比較于傳統壓力機，伺服壓機采用伺服電機作為驅動元件，可以對電機運動進行精確控制，從而實現高精度、高柔性的壓裝工藝曲線規劃。

曲柄滑塊機構作為一種傳統的壓力機傳動機構，常見于由傳統壓力機改裝得到的伺服壓力機上。曲柄滑塊機構在運動過程中，由于大質量沖頭滑塊直線運動速度不均勻的緣故，使得傳動機構折算到伺服電機軸上的轉動慣量發生變化，而現有的伺服壓力機多采用傳統的定參數PID控制器來進行閉環運動控制，因此，對于變轉動慣量控制對象的適應性較差。

針對系統變轉動慣量控制以及廣義的線性時變系統問題，可以采用不依賴于精確對象模型的控制方法，包括基于神經網絡的PID參數自整定研究[1-7]、模糊控制方法[8-9]、自抗擾控制器研究[10]等；也可以采用系統模型辨識的方法，如卡爾曼濾波辨識轉動慣量的研究[11]、基于模型參考自適應的轉動慣量辨識研究[12]、采用自適應控制律辨識摩擦系數補償被控對象[13]、通過實驗方法辨識得到永磁同步電機參數值，再使用二階系統模型進行電流環、速度環整定[14]。

本研究認為通過對曲柄滑塊機構進行運動學分析，確定曲柄轉動到各個位置區間時滑塊對電機軸的等效轉動慣量，從而得到各個位置區間上對應的速度環被控對象模型，并相應地調整速度環PI控制參數，最終可以實現伺服壓力機的變轉動慣量自適應控制。

對于傳統的運動控制器與伺服驅動器分離的結構，由于被控對象經過驅動器與控制器相連，其各個實際參數都在經過伺服驅動環節的處理后才進入控制環，根據實際被驅動機構抽象出的對象模型與控制環中的對象模型之間存在著復雜的轉換關系，如果直接等價兩者，會導致計算出的PI參數準確性較低，需要對實際機構進行模型辨識。而新型的驅控一體化設備將控制器和驅動環節集成在一起，實際對象的相關參數可以比較真實地反映到控制環路的對象模型中，因此可以大大提升理論計算PI值的準確度；同時，一體化的設計還可以簡化系統結構、節省空間，還可以避免配線復雜的問題[15]。

本文主要分析電流環、速度環控制參數的整定方法，并基于驅控一體化設備搭建運動控制平臺，以永磁同步電機帶動不同轉動慣量的盤狀配重來進行實驗；同時，在電機運動過程中調整運動控制參數的值，以驗證當系統實際模型與系統控制參數不相適應時，可以在線整定控制參數的值，使系統的跟隨性能趨于理想，從而為根據位置區間分段改變PI以適應不同轉動慣量值的控制方法作一個理論鋪墊。

1 曲柄滑塊機構轉動慣量變化分析

針對運動中的曲柄滑塊機構，須對折算到電機軸上的等效轉動慣量的變化進行分析建模。

曲柄滑塊機構的結構簡圖如圖1所示。

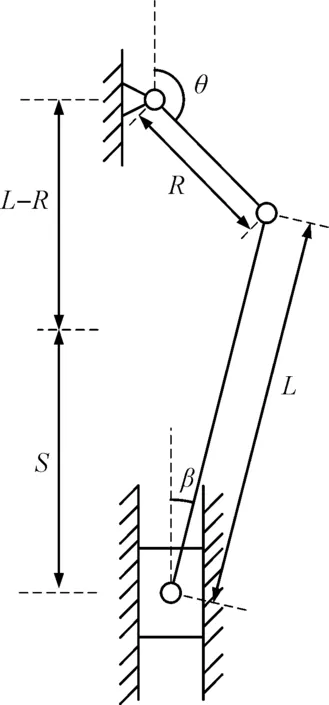
圖1 曲柄滑塊機構簡圖R—曲柄長度；L—連桿長度；θ—曲柄轉角；β—連桿與滑軌夾角；S—滑塊位移

根據圖1幾何關系，可推得滑塊位移、曲柄轉角和連桿與滑軌夾角之間的關系為：

式中：λ—曲柄與連桿的長度之比。

根據三角函數的內在關系，再結合式(1)可以得到：

(2)

當λ取0.08～0.2時，有約等關系如下：

(3)

將式(3)代入式(1)中，可得到滑塊位移與曲柄轉角之間的關系式：

(4)

對等式兩端求導，可得到滑塊直線速度與曲柄轉速之間的關系式：

(5)

式中：ωf—曲柄轉速；v—滑塊直線運動速度。

等效轉動慣量折算采用等效動能原則，即等效轉動慣量增加到電機軸上的動能應當與滑塊直線運動的動能相等，即：

(6)

式中：ω—電機軸轉速；ωf—曲柄轉速；v—滑塊直線運動速度；J′—滑塊等效轉動慣量；m—滑塊質量；n—傳動比。

結合式(5，6)可以得到等效轉動慣量關于曲柄位置的表達式：

(7)

由上式可以看到，當滑塊質量較大時，隨著曲柄轉角θ的變化，等效轉動慣量J′的值也會發生較大的改變，且隨著曲柄位置θ的確定，等效轉動慣量的值也相應確定，因而可以在某一位置區間內，將電機及曲柄滑塊機構簡化為確定轉動慣量的一階慣性環節，并作為速度環被控對象。

2 控制系統參數整定

2.1 系統電流環控制參數整定

根據理想的永磁同步電機交直軸矢量控制模型，可得到交直軸電流電壓方程為：

(8)

(9)

式中：ud—直軸電壓；id—直軸電流；Ld—直軸電感；uq—交軸電壓；iq—交軸電流；Lq—交軸電感；R—電機繞組電阻；ωe—電機電角速度；Ψf—永磁體磁鏈。

對式(9～10)作拉普拉斯變換，忽略交、直軸耦合和感應電動勢，可以得到：

(10)

(11)

采用PI控制器實現電流環控制，可以得到電流環結構簡圖，如圖2所示。

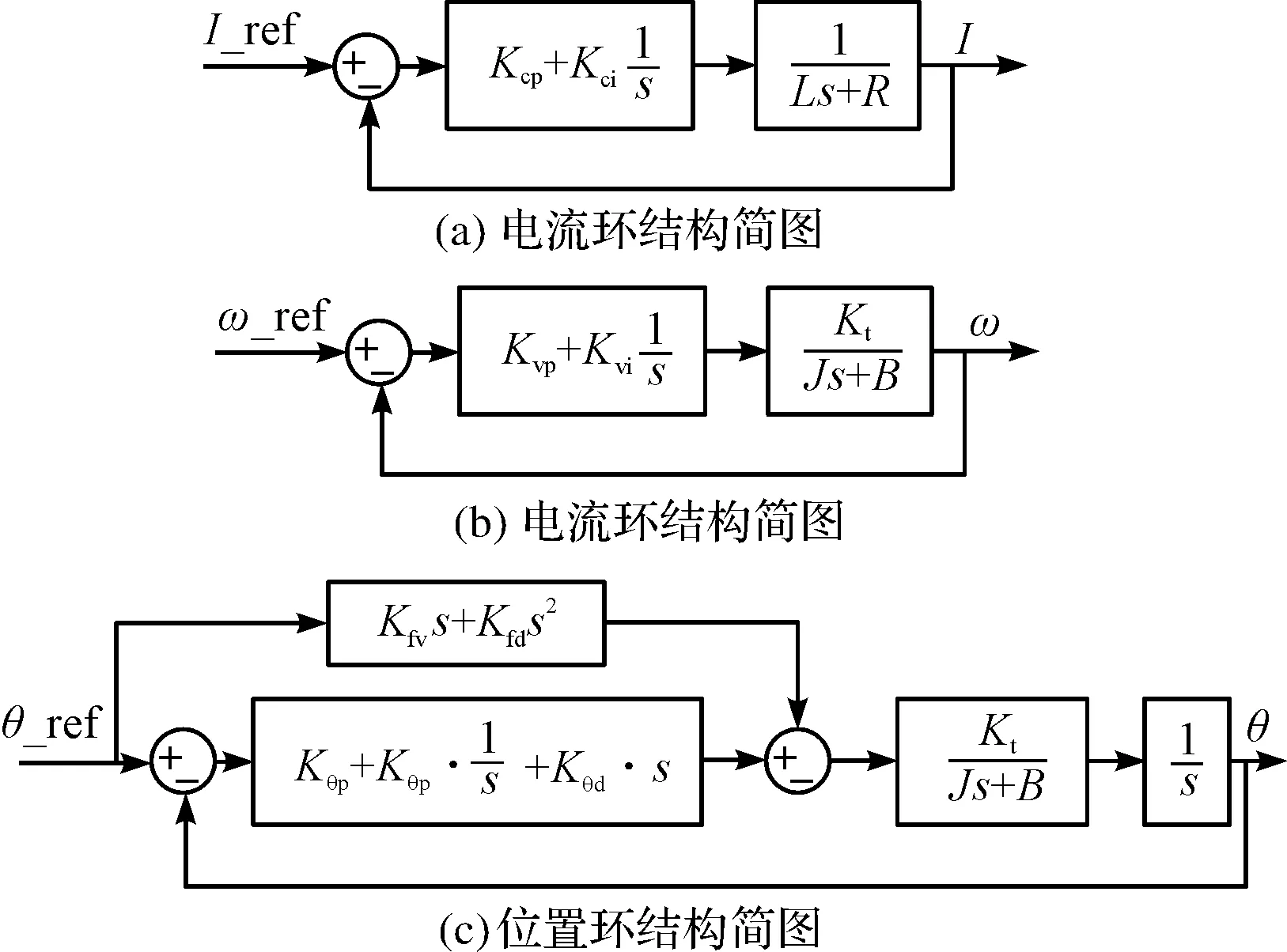
圖2 控制器三環結構簡圖

由圖2(a)可知：電流環理論上的總傳遞函數如下：

(12)

從式(12)可知，電流環的總傳遞函數滿足有零點二階系統傳遞函數的基本形式，即：

(13)

式中：ζ—系統阻尼比；ωn—系統自然頻率；τ—系統零點的倒數取負值。

對于一個二階系統，可以通過配置其零、極點來改變系統的控制性能；其中，極點配置是通過調節系統阻尼比、自然頻率來完成的；同時，由式(12)可知當電流環傳遞函數極點確定時，其PI參數也唯一確定。因此，電流環PI參數的整定是通過確定系統阻尼比、自然頻率實現的。

結合式(12～13)可以得到電流環PI參數與電流環阻尼比、電流環自然頻率之間的關系式：

(14)

式中：ζc—電流環阻尼比；ωnc—電流環自然頻率。

2.2 系統速度環控制參數整定

dq坐標系下永磁同步電機電磁轉矩方程為：

Te=P(1.5Ψfiq+(Ld-Lq)idiq)

(15)

(16)

式中：J—系統總轉動慣量；B—電機粘性摩擦系數；P—電機極對數；ω—電機機械轉速；Te—電磁轉矩；TL—干擾轉矩。

如不考慮電機凸極性，假定交、直軸電感相等，則式(15)可簡化為：

Te=1.5PΨfiq=Ktiq

(17)

采用PI控制器對電機速度環進行控制，結合式(16～17)，并考慮到電流響應比電機速度響應要快得多(約一個數量級左右)。因此，在討論速度環時，可以將內部的電流環簡化為1，由此簡化得到的速度環結構簡圖如圖2(b)所示。

由圖2(b)可得速度環的理論總傳遞函數為：

(18)

與電流環相同，速度環傳遞函數也滿足有零點二階系統的標準形式。因此，可以得到速度環PI參數的整定表達式為：

(19)

式中：ζv—速度環阻尼比；ωnv—速度環自然頻率。

從式(19)中可以看到：在速度環阻尼比、自然頻率確定的情況下，當系統的總轉動慣量確定時，速度環PI的值也就隨之確定。

對于曲柄滑塊機構傳動的伺服壓力機，其系統總轉動慣量近似等于電機軸自身和沖頭滑塊折算到其上的轉動慣量之和，即：

J=Jm+J′

(20)

式中：Jm—電機軸轉動慣量，Jm為常數；J′—滑塊等效轉動慣量。

其中，沖頭滑塊折算慣量J′的值是關于曲柄轉角的函數，如式(7)所示。如果伺服電機與曲柄的傳動比為1，則電機位置與曲柄轉角相等；將電機一周的轉動分割為多個位置區間，每個區間近似為一個位置值，則在ζv、ωnv確定的情況下，根據式(7，19，20)可以計算得到一組相應的速度環PI參數。因此，伺服壓力機控制系統的速度環參數可以在電機轉動過程中，依據電機位置在多組參數間進行變換，從而實現在線整定。

2.3 阻尼比ζ和自然頻率ωn的確定

從速度環、電流環的傳遞函數來看，兩者均為有零點的二階系統。由于零點的影響，即使阻尼比ζ>1時，系統單位階躍響應仍然可能具有10%以上的超調。因此，可直接考慮過阻尼情況下有零點二階系統ζ、ωn的確定。

(21)

由式(21)可知：若要求系統無超調則可令，進而得到下式:

(22)

對于有零點的二階系統，可以得到系統帶寬和系統自然頻率、阻尼比的關系，即:

ωb=

(23)

其中，τ與ζ、ωn、δ的關系如下：

(24)

根據式(22～24)可以得到無超調系統自然頻率與帶寬的關系式：

(25)

其中，δ的取值規則如下：對于電流環，δ的值等于繞組阻值R與電感L的比值，為常數；對于速度環，δ的值等于系統總轉動慣量J與摩擦系數B的比值，也是曲柄轉角θ的函數。

綜上所述，對于速度環、電流環，均可先指定系統帶寬，再根據式(22，25)由帶寬得到ζ、ωn的值。其中，電流環的帶寬通常為速度環的2～10倍。

2.4 系統位置環控制參數整定

系統位置環采用了前饋補償與PID控制器結合的控制方式，使用速度和加速度量乘以前饋系數后，對電流進行補償。

從圖2(c)可以得到位置環傳遞函數為：

(26)

式中：Kfv—速度前饋系數；Kfa—加速度前饋系數。

為了簡化系統，一般取加速度前饋Kfa和Kθi、Kθd為0。則系統傳遞函數Фθ可轉化為：

(27)

由式(27)可知：位置環傳遞函數符合有零點二階系統的基本形式，其極點可表示如下：

P1、2=

(28)

由于系統轉動慣量J、粘性摩擦系數B、轉矩系數Kt和Kθp均為正數，明顯系統極點總具有負實部，系統位置環穩定。在式(27)中，由于B/J的值一般較小，Kθp的值不可取得太大，否則會使得系統固有頻率太大；而阻尼比太小，導致振蕩。一般來說，Kθp的取值在0～1之間。

同時，由于系統使用速度前饋來補償位置，速度環的性能調整對于位置環的跟隨效果有著直接的影響。

3 電流環、速度環調試實驗

為了驗證整定得到的PI參數是否有效，本文搭建了簡易的伺服控制平臺。平臺采用固高科技開發的GTSD14系列驅控一體化伺服驅動器對永磁同步電機進行控制，并準備了不同大小的配重以改變系統的轉動慣量，同時觀察其電流環、速度環、位置環的響應性能。

實驗平臺外觀如圖3所示。

圖3 實驗平臺及控制系統硬件環境

所選永磁同步電機的電機參數如表1所示。

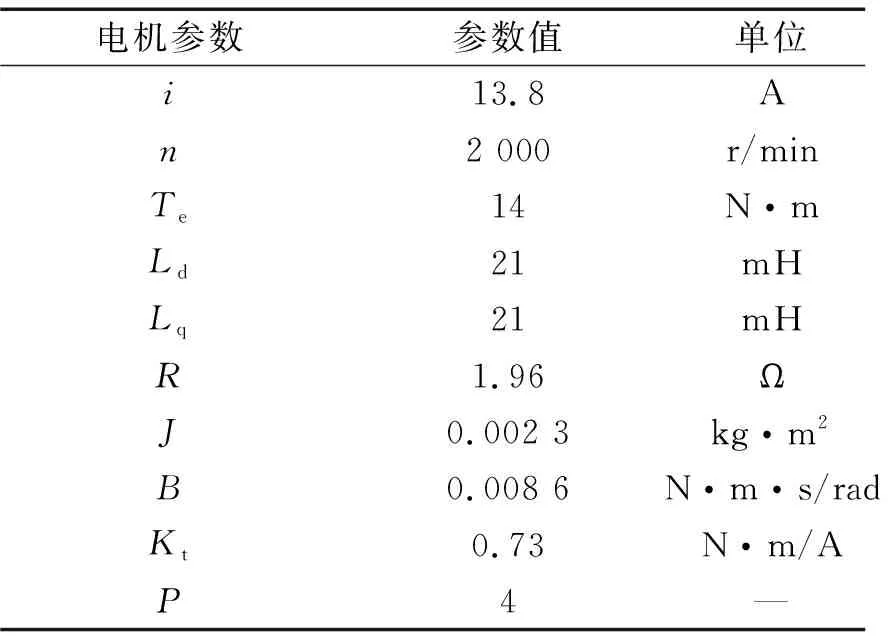
表1 永磁同步電機參數

配重為圓形鐵盤，實驗中使用了兩個大小不同的鐵盤，記為大盤和小盤。兩盤厚度均為15 mm，小盤直徑為120 mm，大盤直徑為180 mm，其外觀如圖3(b)所示。

圓盤的轉動慣量為：

(29)

式中：J—圓盤轉動慣量；m—圓盤質量；r—圓盤半徑；h—圓盤厚度；ρ—圓盤密度。

取圓盤密度為7.9×103kg/m3，根據式(29)可以計算得到小盤轉動慣量為0.002 4 kg/m2，大致上與電機自身慣量相等；大盤轉動慣量為0.012 2 kg/m2，大約是電機慣量的5倍。

由式(19，22，25)可知，保持速度環帶寬不變，且默認速度環無超調，則對于每一個確定的轉動慣量，可以得到一組相應的PI參數。

該實驗中，首先以電機空載時的慣量得到與之相適應的PI參數，記為空載參數組，再根據電機帶動大、小盤時系統實際轉動慣量得到相應的PI參數組；使電機分別帶動大、小盤運動，并在系統運動中改變速度環控制參數的值，使之從空載組轉變至大、小盤組，同時觀察速度環、位置環響應的改變，如果響應能力的改變與動態性能指標規定的相符，則可證明當速度環PI參數與系統真實慣量不相適應時，可以在線整定PI參數的值使之適應系統。從而說明對于變轉動慣量壓力機，分段改變PI參數以保持響應性能的相對恒定，在理論上具有可行性。

3.1 電流環調試

根據表1可知：電機交直軸電感約為0.021 H，且繞組電阻為1.96 Ω，因而可以得到后者與前者的比值δ≈93。取電流環帶寬為600 Hz，轉換至角頻率有ωb=3 769.9 rad/s；根據式(22，25)可解得ωn=593.2 rad/s，ζ=3.26；根據式(14)可以計算得到kp=79，ki=7 389，之后在實際平臺上驗證了PI參數的性能。

取參考電流值為6 A，電流響應結果如圖4所示。

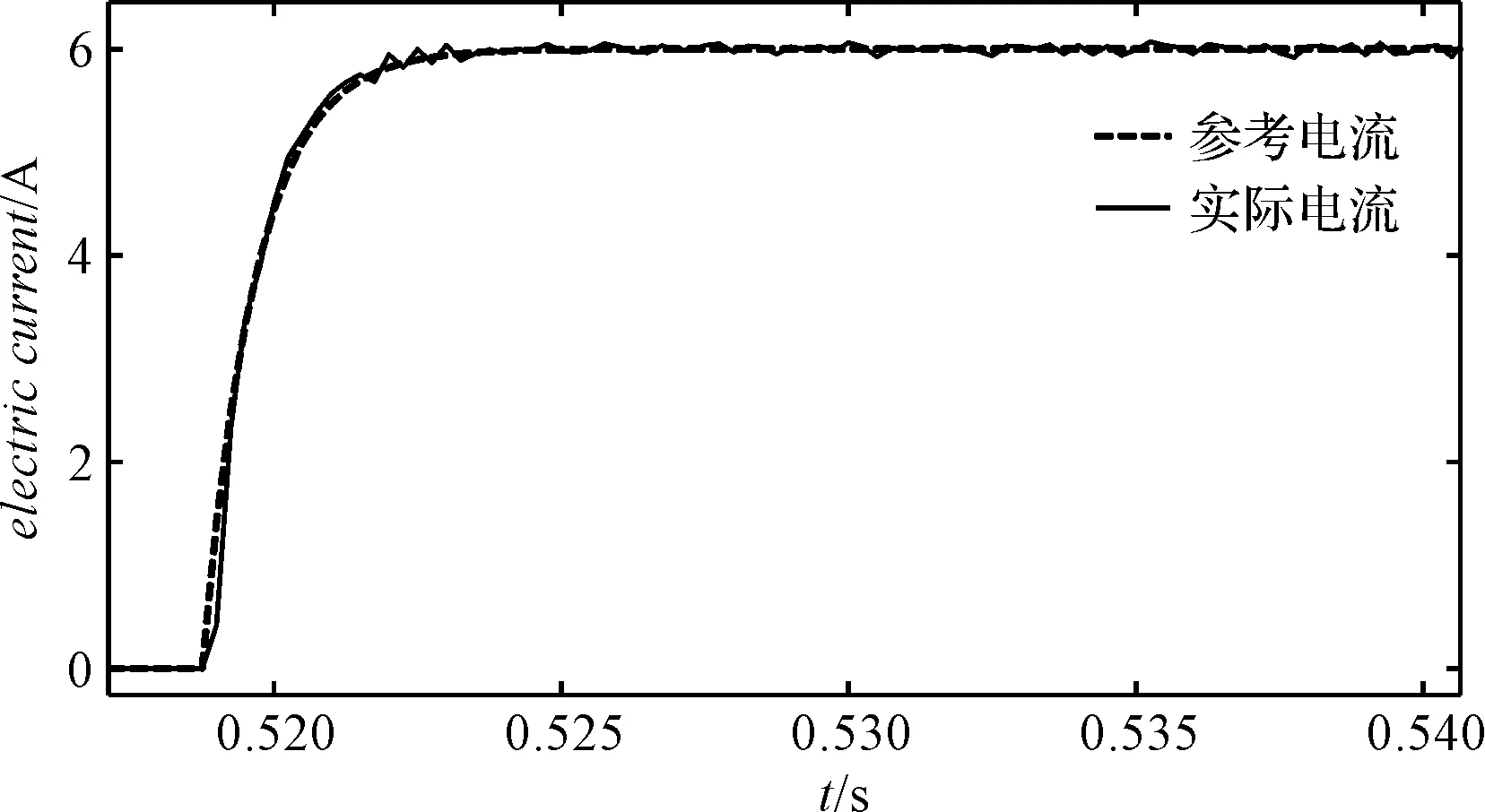
圖4 fb=600 Hz時電流響應上升狀態趨勢圖

從圖4中可以看到：實際電流響應的超調量大致為0，最大不超過2%，基本符合響應無超調的要求；且電流上升迅速，實際電流較規劃電流滯后不超過0.2 ms；同時，實際電流的穩態波動值保持在1%～2%。

3.2 速度環調試

3.2.1 帶寬為100Hz時的速度環測試

取速度環帶寬為100 Hz，可以得到ωb=628.32 rad/s。已知電機實際轉動慣量J=0.002 3 kg/m2，粘性摩擦系數B=0.008 6 N/ms，比值δ為3.74，則根據式(22，25)可以計算得到速度環阻尼比ζ=6.52，固有頻率ωn=48.47 rad/s。進而根據式(19)可以計算得到理想PI參數，記為kp空載100 Hz,ki空載100 Hz。其中，kp空載100 Hz=1.98，ki空載100 Hz=7.40。

驅控一體中，實際使用的速度環PI參數為整數量，其與理論計算PI之間存在著一種簡易的當量轉換關系，即：

(30)

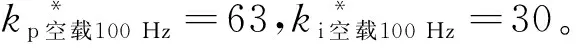
電機速度環測試相關結果如圖5所示。

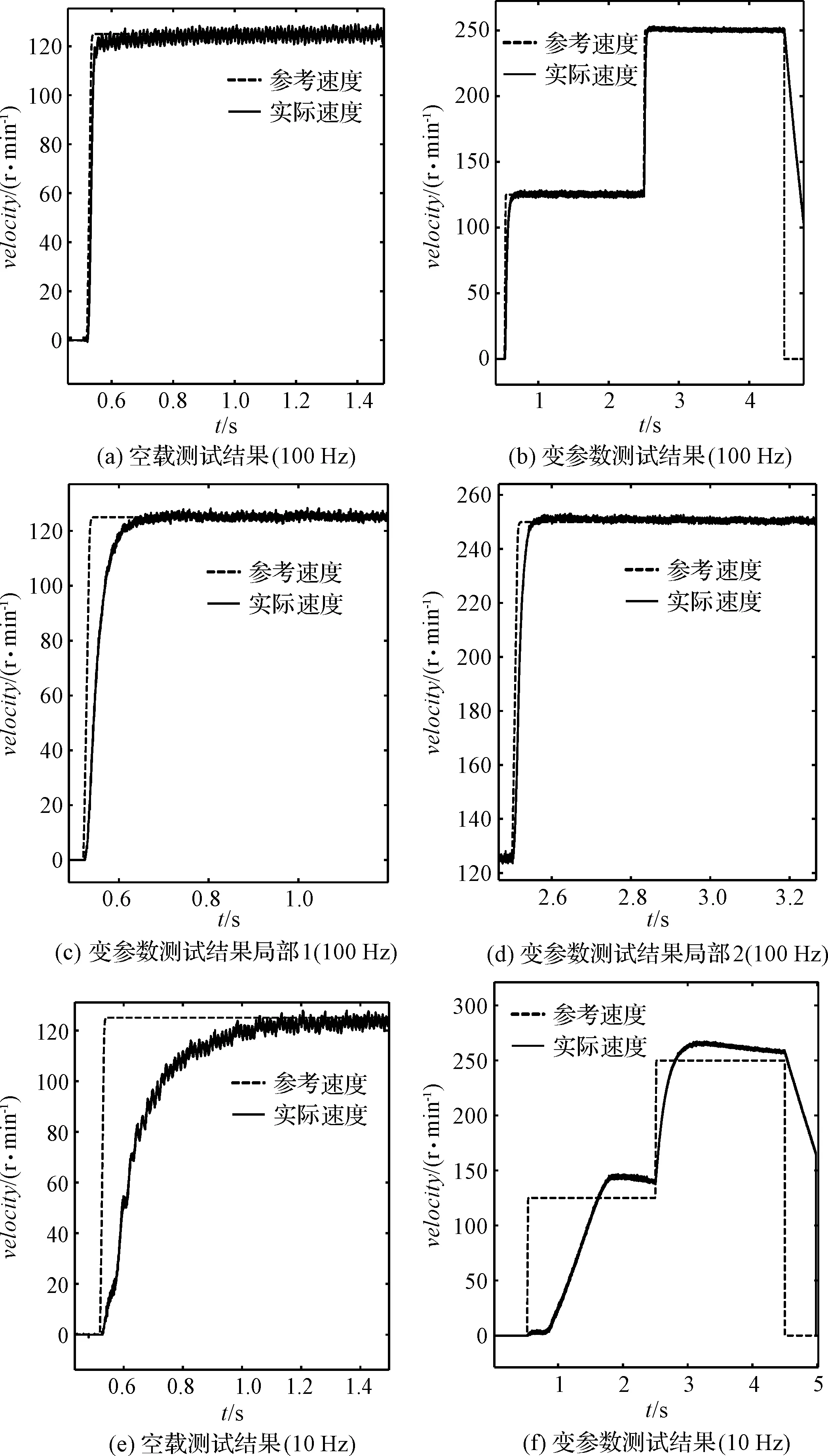
圖5 速度環測試結果

空載測試后，加裝小盤進行變參數測試，具體過程如下：測試開始后延時0.5 s啟動電機，參考速度為125 r/min，此時仍采用空載時的PI參數；測試時間1.5 s時控制參數切換為與實際系統相適應的小盤組PI；測試時間2.5 s時修改參考速度為250 r/min；測試時間4.5 s時參考速度為0，電機去使能，測試結束。

從變參數測試的兩次速度上升過程中可以看到，加裝小盤后，仍使用空載PI參數，使得系統跟隨滯后時間大大拉長了，達到了25 ms(取達到目標速度60%所用時間)；而PI參數調整為與小盤相適應的值后，該時間縮短至15 ms。

在兩組參數的作用下，系統都幾乎沒有超調，但調整后的PI參數明顯更符合帶寬的要求。

3.2.2 帶寬為10 Hz時的速度環測試

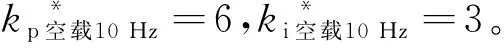
在10 Hz超低帶寬下，電機速度響應的滯后很大，大約為150 ms～200 ms，是理想滯后時間的2～1.5倍。

加裝大盤后的變參數測試，其過程與小盤類似，從中可以看到：兩組參數作用下的速度響應都有明顯超調，但考慮到電機規劃轉速提升至250 r/min時，實際轉速還未收斂至125 r/min，如果減去起始時實際速度和規劃速度的差值，那么大盤PI參數作用下速度曲線的超調量也只有2%～3%左右，其滯后時間大約為150 ms左右；在空載參數作用下，速度響應超調量為16%，滯后時間約為700 ms～800 ms，遠遠不能滿足帶寬要求。

3.3 速度環參數變化對電機位置跟隨的影響

由于伺服壓力機優化的最終目的是提升位置控制的精度，需要討論速度環運動控制參數調整對系統位置控制的影響。

在線調節速度環PI參數時，電機的位置跟隨曲線如圖6所示。

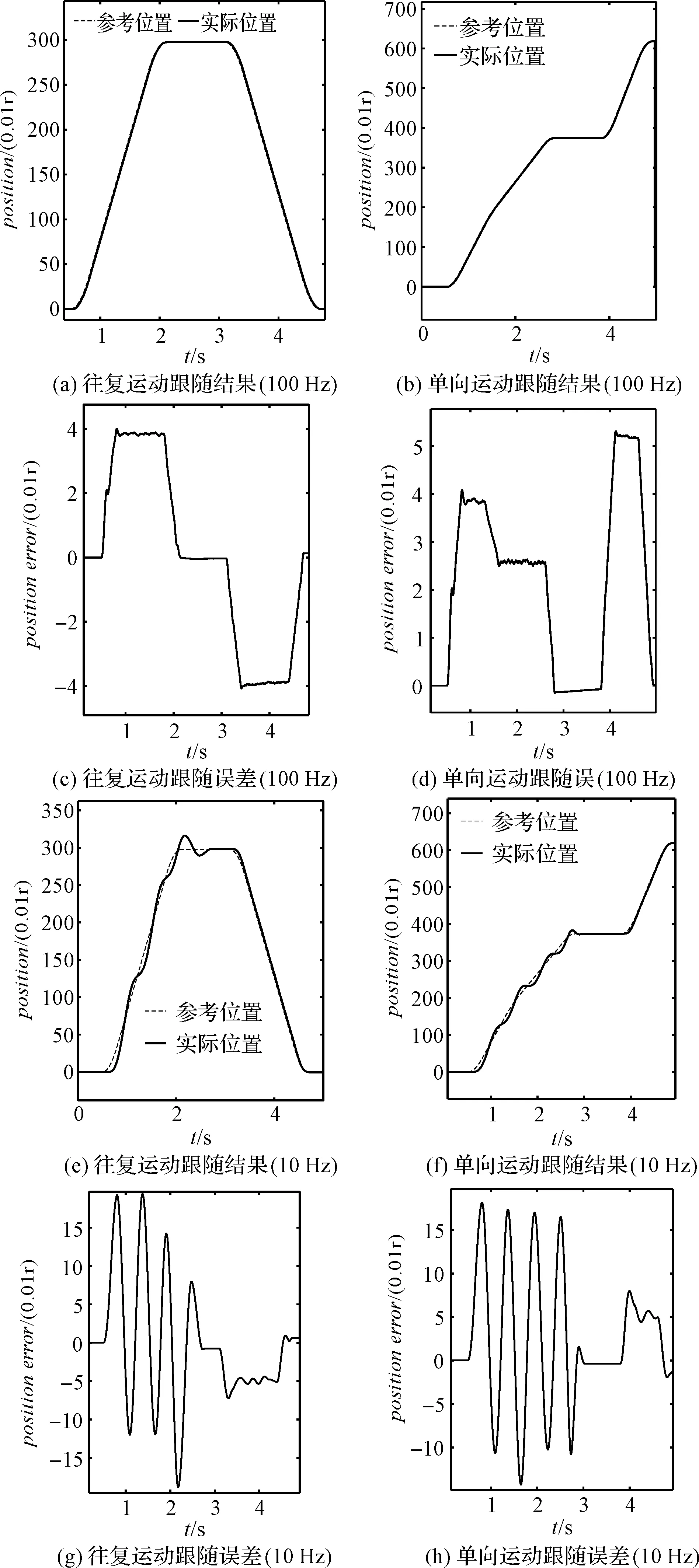
圖6 電機位置跟隨結果

本研究取位置環kp為0.3，并使電機模擬伺服壓力機多段行程運動；同時，調整速度環參數，觀察系統位置跟隨狀態的變化。調整過程與變參數速度環測試時類似：電機分別帶動大、小配重盤轉動，同時系統PI參數從空載值逐步調整至與系統實際慣量相匹配的值。該實驗中取切換時間為2.4 s，在0.3 s內逐步調整完成。

圖6中，運動系統控制參數均由kp*=63、ki*=30轉變至127、30。由此可以看到：由于轉動慣量的變化較小，空載參數作用下的運動，其位置曲線也非常良好；加裝小盤的運動中，可以看到自2.4 s后，偏差的波動減小，到返程運動時，偏差值保持平穩。

帶寬為10 Hz時，電機加裝大盤后進行往復運動以及單向多段運動中，速度環PI參數由kp*=6、ki*=3轉變至40、3。由此可以看到：由于實際慣量與電機空載時已經發生了巨大變化，在空載參數作用下，電機位置大幅波動；而從2.4 s后位置曲線迅速趨于平滑。

從加裝大盤時，兩種運動中實際位置與規劃位置偏差值的變化可以看到：當轉動慣量發生較大偏差時，在線調整PI參數的值可以顯著地改善系統的位置跟隨性能。

4 結束語

本研究基于確定的轉動慣量整定電流環、速度環PI控制參數，并在實際運動控制平臺上進行了實驗。實驗結果表明：對于轉動慣量確定的被控對象，二階系統整定得到的PI參數可以滿足電流環、速度環控制要求；且在相同帶寬要求下，當系統實際轉動慣量與整定參數控制性能不匹配時，可以對參數進行在線整定，使其適應系統的真實慣量，同時也表明對于速度環參數的優化可以直接改善系統位置環的跟隨性能。

總體來說，實驗結果說明了根據機構各幾何位置轉動慣量計算自適應PI參數，以提高壓力機位置控制能力的方法在理論上具有可行性。

在下一階段，本研究將采用真正的曲柄滑塊機構進行實驗，以進一步驗證二階理論計算自適應PI的實際效果。

參考文獻(References):

[1] YUAN Rui-bo, SUN Chun-geng, BA Shao-nan, et al. Analysis of position servo system of pneumatic manipulator based on RBF neural network PID control[C].2010 International Conference on Web Information Systems and Mining,Piscataway: IEEE, 2010.

[2] LI Xin, ZHU Yu, YANG Kai-ming. Self-adaptive composite control for flexible joint robot based on RBF neural network[C]. 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems, Piscataway: IEEE, 2010.

[3] WAI Rong-jong, LIN Hsin-hai, LIN Faa-jeng. Hybrid controller using fuzzy neural networks for identification and control of induction servo motor drive[J]. Neurocomputing, 2000, 35(2):91-112.

[4] CHEN Chaio-shiung, LIN Wen-chi. Self-adaptive interval type-2 neural fuzzy network control for PMLSM drives[J]. Expert Systems With Applications,2011,38(12):14679-14689.

[5] 張通通.仿人機器人關節負載自適應伺服控制[D]. 北京：北京理工大學機電學院，2015.

[6] 蘇德淳,王仲根.基于柔性神經網絡模糊PID的永磁同步電機調速研究[J]. 制造業自動化，2018,40(10):77-80.

[7] 高旭東.永磁同步電機智能控制系統研究[D]. 石家莊：石家莊鐵道大學機械工程學院，2016.

[8] 張曉光,柳同升,刑旭東.基于模糊PI并聯控制永磁同步電機轉動慣量問題研究[J]. 電源學報,2014(4):35-40, 46.

[9] 廖雄志.基于最優模糊PID永磁同步電機調速系統的研究與實現[D]. 株洲：湖南工業大學電氣與信息工程學院,2018.

[10] 張德民,徐仕源.基于自抗擾的自適應控制在永磁同步電機控制中的應用[J]. 電機與控制應用,2017, 44(4):70-73.

[11] 劉 濤.交流伺服系統轉動慣量實時辨識與控制器研究[D]. 深圳：哈爾濱工業大學(深圳)機電工程與自動化學院,2011.

[12] 董烈超.交流伺服系統轉動慣量辨識及其應用[D]. 武漢：武漢科技大學信息科學與工程學院,2016.

[13] 王端娟,梅志千, 李向國，等.機電伺服系統非線性摩擦自適應補償的研究[J]. 中國電機工程學報,2012, 32(36):123-129.

[14] 梅志千,張 璇,王 蕊.粘著控制中的交流永磁同步電機調速控制研究[J]. 電機與控制學報,2009, 13(6):867-873.

[15] 祁玫丹.嵌入式驅控一體的Delta機器人控制器研發[D]. 西安：西安建筑科技大學機電工程學院,2017.