具有miRNA調控的癌癥網絡模型的動力學分析

許慧潔，易秀，楊曉燕，王喬鈺

(蘭州交通大學 數學系，甘肅 蘭州 730070)

1 引言

在細胞中，生物的遺傳信息被儲存在DNA中，DNA被世代傳遞。為了深入了解這些過程，數學模型一直被用于基因調控網絡的研究。但是最近的研究表明，只有大約2%的基因序列可以被表達成蛋白質，因此在建立遺傳調控網絡的數學模型時，還需要考慮一些別的因素，近年來越來越多的研究揭示了ncRNA在人體中的重要作用，而本文所考慮的miRNA簇是一種特殊的ncRNA。本文所討論的模型是基于文獻[1]的系統(1)：

(1)

其中，u表示Myc和E2F混合物的種群密度，v表示miRNA簇的種群密度，并且假設模型中出現的所有參數對于生物學來說都是有意義的(即都是正的)。常數σ表示通過細胞外介質中的轉錄途徑產生的蛋白質，δ表示蛋白質的降解速率，μ表示獨立于Myc和E2F的miRNA的轉錄，k2是蛋白質的轉錄速率，r是miRNA降解的速率。當作者引入變量后，減少了參數，得到了系統(2):

(2)

當我們考慮時滯對系統(1)的影響后，便得到了下面系統(3)：

(3)

假設E*=(u*,v*)是系統(2)的正平衡點，很容易得到v*=u*+1，且u*,v*是關于u的方程G(u)=u3+m2u2+m1u+m0的正根，其中m0=-α(a+b)m1=α+b(1-α),m2=b-(α+k)。在文獻[1]中，關于系統(2)的正平衡點得到了以下結論：

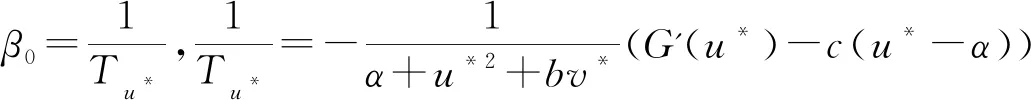
Ⅰ 當系統(2)只有一個正平衡點時，這唯一的正平衡點E*在0<β<β0，是漸近穩定的。當β<β0時，E*是不穩定的，當β=β0時，系統(2)在E*附近進行Hopf分支。

Y.L.Song等在實驗中觀察到了miRNA對Myc和E2F的抑制作用具有一定的時間延遲，并且Myc和E2F在自我促進時信號的傳輸需要時間；Song等人針對這一實驗現象，提出了時滯微分方程，并給出了正平衡解的存在性，全面分析了雙穩態的動力學。T.H.Zhang[2]等研究了一個具有時間延遲的基因表達模型，并給出了存在導致Hopf分支的時間延遲臨界值。Nikolov[3]等人給出了時間延遲在miRNA動力學的調節中以及別的調節網絡中更具有穩定性的作用，但是，他們沒有徹底研究這種穩定作用取決于延遲的長度。因為miRNA在多種細胞形成的過程中起著重要的作用，因此很多數學家通過建立數學模型來研究miRNA與癌癥細胞之間的關系，如想要對此模型有更多的了解可以參考文獻[4-8]。本文考慮實驗中另外的時間延遲現象，即考慮蛋白質在轉錄和降解的過程中存在的時間延遲會對系統穩定的正平衡解產生的影響。

2 時滯引起的穩定的平衡點失穩

這部分主要研究系統(2)只有一個正平衡解時，且這個正平衡解是穩定的情況下時滯對于這個正平衡解產生的影響。

用E*=(u*,v*)來表示系統的正平衡解，將系統(3)在E*處線性化可得：

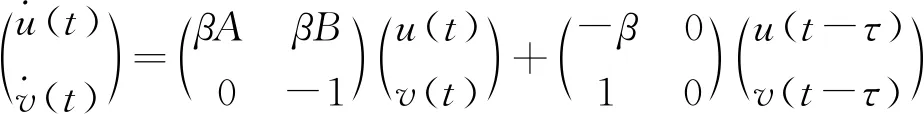
(4)

其中

線性化系統的特征方程為：

λ2+(1-βA)λ-βA+β(λ+1-B)e-λτ=0

(5)

我們假設λ=iω(ω>0)是特征方程的根，將λ=iω代入特征方程得到以下方程

-ω2+(1-βA)iω-βA-β(cosωτ-isinωτ)iω+β(1-B)(cosωτ-isinωτ)=0

將上述方程分離實部和虛部，可得下列方程組：

(6)

整理可以得到：

ω4+(1+β2A2-β2)ω2+β2(A2-(1-B)2)=0

(7)

令Z=ω2，則式(7)可化為：

Z2+(1+β2A2-β2)Z+β2(A2-(1-B)2)=0

從上式很容易得到下面引理：

定理1當Δ=(1+β2A2-β2)2-4β2(A2-(1-B)2)>0,1+β2A2-β2<0時，方程(7)有一個正根。

然后由方程組(5)可以得到關于sinωτ和cosωτ的表達式

則τ的值可以得出：

令h(Z)=Z2+(1+β2A2-β2)Z+β2(A2-(1-B)2)=h(ω2)

由文獻[9]得

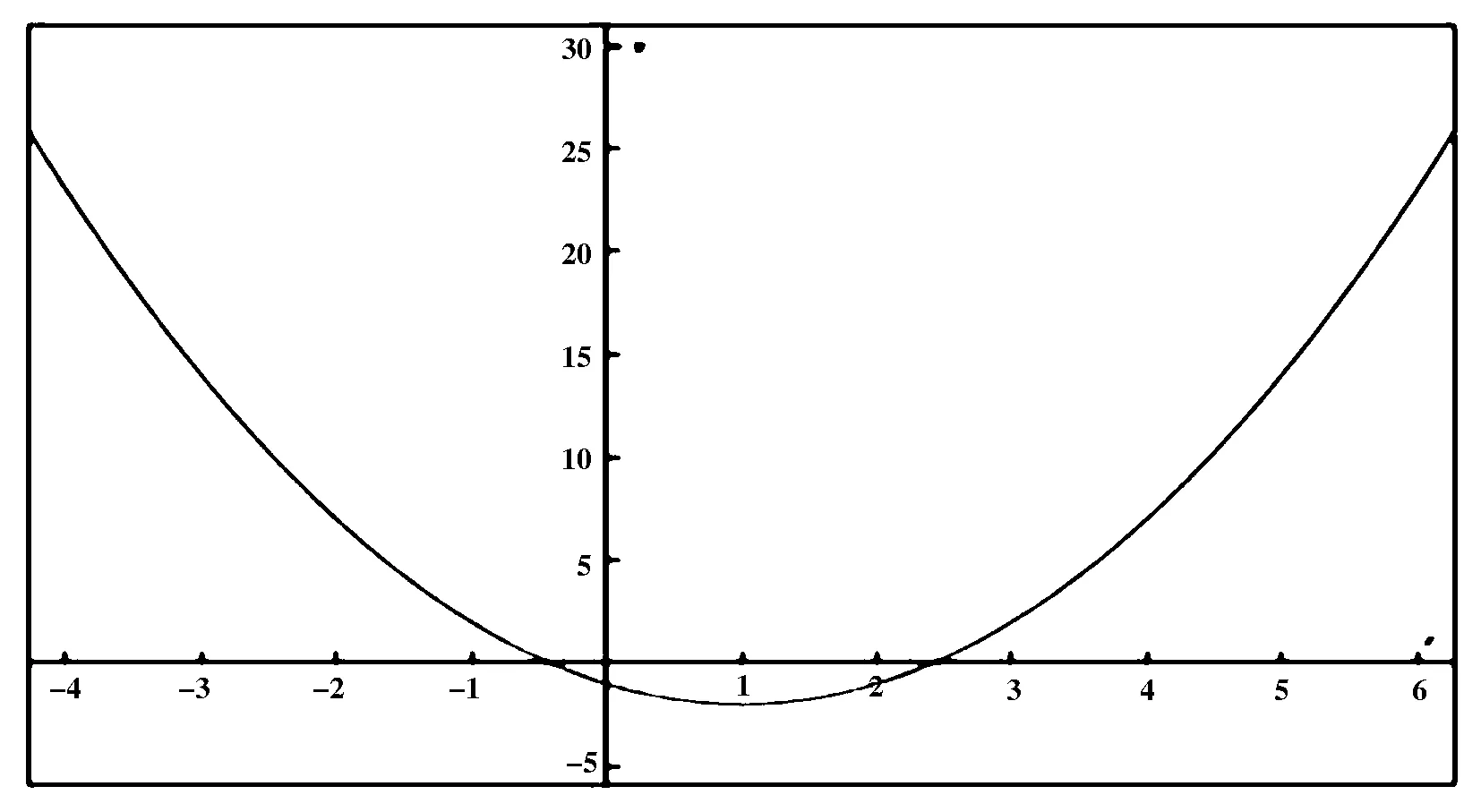
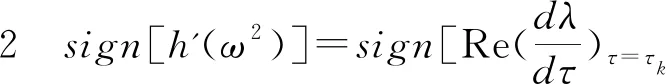
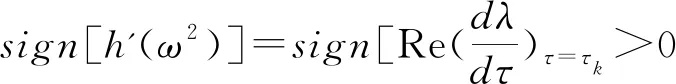
由上述橫向性條件得到下面的定理：

定理2假設ω和τj是由式(7)、式(8)定義的,E*是穩定的正平衡解。在條件1+β2A2-β2<0成立的情況下：

(1)對任意的τ∈(0,τ0)時,系統(3)的平衡解E*是穩定的，當τ∈(τ0,+∞)時E*是不穩定的。

(2)當τ=τj(j=0,1,2,…)時，系統(3)在正平衡解E*附近出現Hopf分支。

3 數值模擬

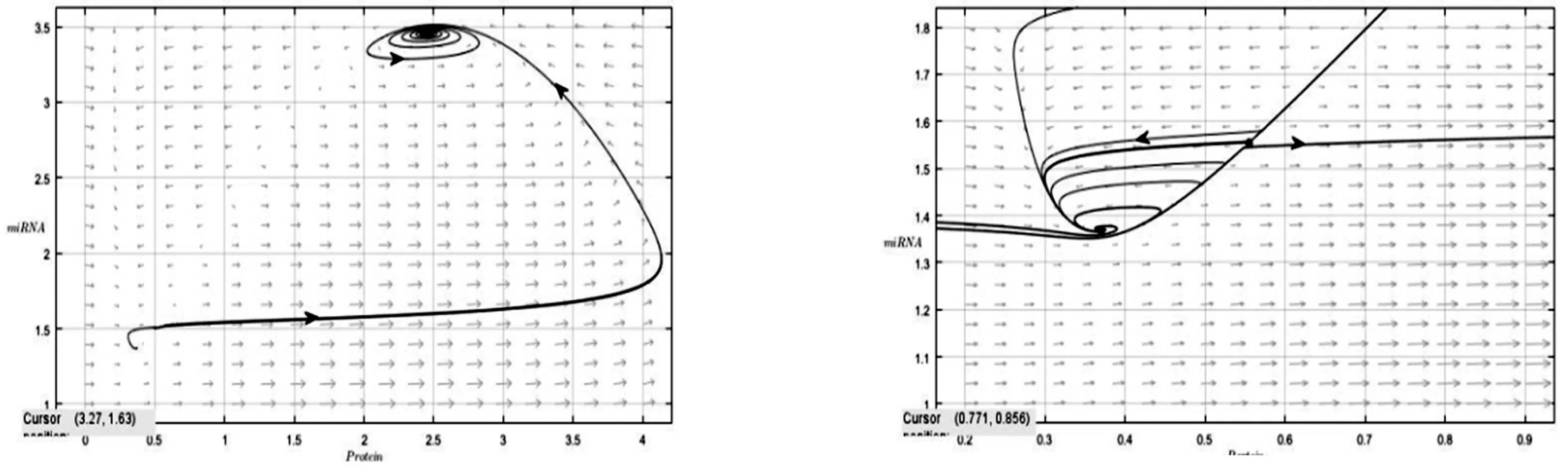
圖1當β=50,α=0.18,a=1,b=1.8,k=5時，系統(2)數值模擬圖2當β=50,α=0.18,a=1,b=1.8,k=5時，系統(2)有兩個正平衡點時的數值模擬

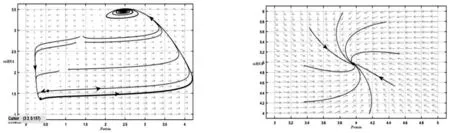
圖3當β=50,α=0.18,a=1,b=1.8,k=5時，系統(2)有三個正平衡點時的數值模擬圖4當β=5,α=0.5,a=2,b=1,k=5時，系統(2)有一個正平衡點時的數值模擬

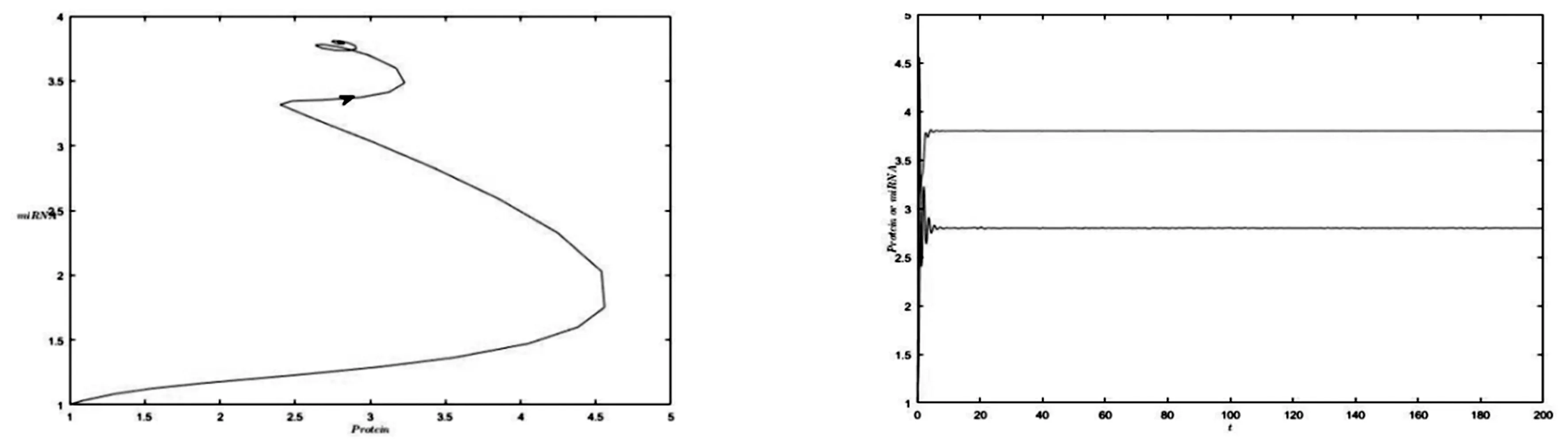
圖5當τ=0.18,β=5,α=0.5,a=1,c=1.8,k=5時，系統(3)的相圖圖6當τ=0.18,β=5,α=0.5,a=1,c=1.8,k=5時，對系統(3)進行的數值模擬

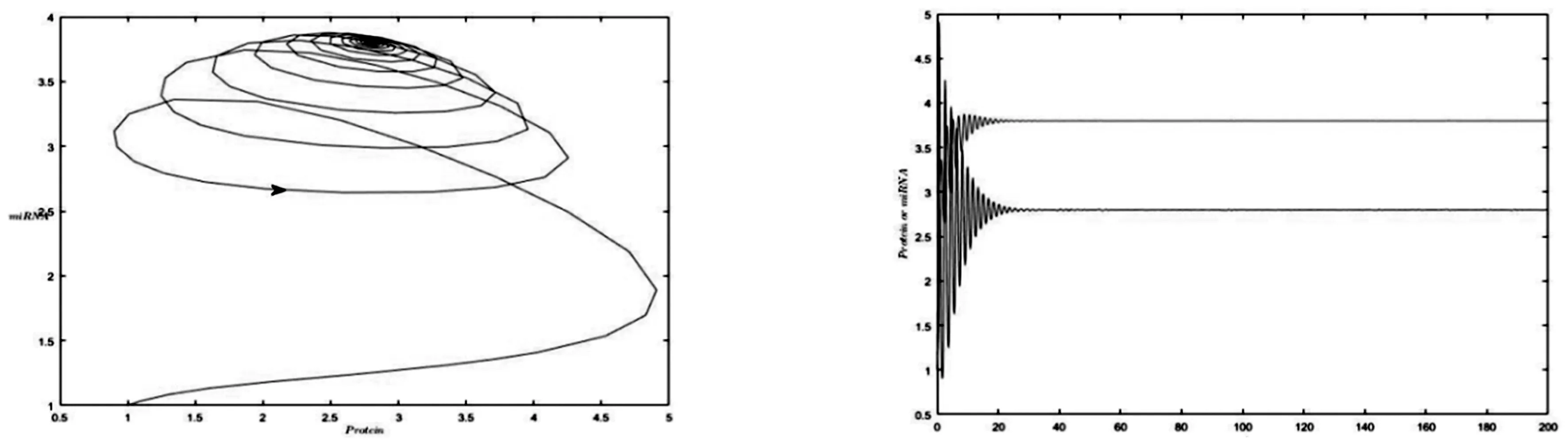
圖7當τ=0.2,β=5,α=0.5,a=1,c=1.8,k=5時，系統(3)的相圖圖8當τ=0.2,β=5,α=0.5,a=1,c=1.8,k=5時，對系統(3)進行的數值模擬

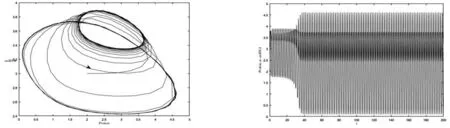
圖9當τ=0.21,β=5,α=0.5,a=1,c=1.8,k=5時，系統(3)的相圖圖10當τ=0.21,β=5,α=0.5,a=1,c=1.8,k=5時，對系統(3)進行的數值模擬

圖11當τ=0.3,β=5,α=0.5,a=1,c=1.8,k=5時，系統(3)的相圖圖12當τ=0.3,β=5,α=0.5,a=1,c=1.8,k=5時，對系統(3)進行的數值模擬

4 結論與討論

本文主要分析了一個具有miRNA調控的基因表達模型，考慮了存在于蛋白質的轉錄和降解過程中的時滯，會對系統產生怎樣的影響。結果表明：系統(2)僅有一個穩定的正平衡解的情況下，時滯會使系統的正平衡解從穩定變為不穩定。更具體地說，如果平衡解在沒有延遲的情況下是穩定的，一個非常小的延遲會使平衡解不穩定，當增加延遲的長度時就可能誘導出穩定的周期解。