數值研究藍寶石光纖參數對產生超連續譜的影響
賈強 譚勇 朱瑞晗
摘 要
超連續譜激光器的發展受到諸多因素的影響,工作物質是影響其發展的主要因素之一,提高激光器輸出譜線的平坦性與強度是其關鍵技術。本文選用數值模擬方法對皮秒脈沖在藍寶石光纖中傳輸過程及產生的SC譜進行研究,其模擬結果表明,當藍寶石光纖的非線性系數增大時,獲得了更寬的輸出脈沖頻譜;當光纖二階色散的數值增加時,頻譜展寬的幅度有上升的趨勢;當光纖長度的數值增大時,超連續譜有展寬的趨勢,但超過一定閾值,平坦度反而下降。在激光器的實際設計中,該結果對產生可見及近紅外超連續譜時,選擇合適的藍寶石光纖參數有重要的參考價值。
關鍵詞
超連續譜;藍寶石光纖參數;非線性效應;數值模擬
中圖分類號: TN248 ? ? ? ? ? ? ? ? ? ? ?文獻標識碼: A
DOI:10.19694/j.cnki.issn2095-2457.2020.04.12
0 前言
非線性光學是一個重要的研究領域,非線性效應及其傳播規律也被廣泛地研究[1-3]。非線性傳播方程描述了在超連續譜產生過程中的各種復雜的非線性效應,包括光纖的群速度色散(GVD)特性、四波混頻(FWM)、受激拉曼散射(SRS)、自相位調制(SPM)、交叉相位調制(XPM)、孤子分裂與孤子自頻移等[4],綜合理解并運用這些效應才可以對超連續譜的展寬進行更好的研究[5]。除此之外,超連續譜產生還涉及物理條件[6],如光纖種類、材質特性與長度,抽運脈沖激光的波長、峰值功率、脈沖寬度與啁啾特性等參量,也會導致輸出的超連續光譜激光脈沖發生明顯變化[7-9]。
本文重點討論同一皮秒脈沖參數下不同藍寶石光纖參數誘導各種非線性效應,進而對輸出超連續光譜的影響。建立多種藍寶石光纖參數特性模型[10],選用分步傅里葉方法數值求解非線性薛定諤方程,并對不同光纖數值參數進行對比分析。討論頻域和時域演化下產生的超連續譜線型[11],分析光譜展寬機制,尋找一種光譜平坦性優化方法。
1 廣義非線性薛定諤方程數值解
對于脈沖寬度小于1ps的脈沖,一般情況下用廣義非線性薛定諤方程(NLSE)來描述其在光纖中的傳輸,得到分步傅里葉的解為:
式中F-1是對振幅A(z,ω)進行傅立葉逆變換。引入變量T=t-β1z,獲得了A(z,T)演化的時域廣義NLSE:
此方程的左側是線性傳輸效應,α作為線性功率衰減,βk為傳播常數β(ω)的泰勒級數展開相關的色散系數。右側表示非線性效應, γ=為非線性系數,其中n2(ω0)為非線性折射率,Aeff(ω0)為有效模式面積。
基于上述傳播方程,通過忽略非線性系數中的n2(ω0)和Aeff的頻率依賴性,得到了廣義非線性薛定諤方程數值解
該等式在頻域中對場A(z,T)進行積分,同時利用變量的變化來轉換到所謂的交互圖像,消除了等式的剛性分散部分。
(3)式中R(T')非線性響應函數,包括電子貢獻和原子核貢獻,若假設電子貢獻是瞬時的,則R(T')函數形式可寫成
在(4)式中,fR為延遲拉曼響應。石英分子振動決定拉曼響應函數光場感應的形式。
(3)式中A(z,T)通常用雙曲正割脈沖線型表征,其表達方程為:
P0為輸入的峰值功率,t0為輸入的持續時間,T是時間窗口分辨長度,也即劃分的格點對應的時間步長。
2 數值模擬與結果分析
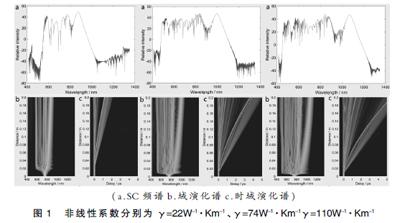
在本節中分別對藍寶石光纖的非線性系數、色散系數、光纖長度進行模擬分析。所采用的藍寶石光纖的詳細參數參考文獻[9],本文模擬改變藍寶石光纖的非線性系數,光纖非線性系數的取值分別如下γ=22W-1·Km-1,74W-1·Km-1,110W-1·Km-1。光纖長度為0.2m,使用的抽運波長為753nm,初始寬度t0=12.5ps,峰值功率為P0=10000W,模擬過程中時間分辨長度T=0.0284ps。
不同光纖非線性系數下,模擬超連續譜的輸出如下所示。
分析模擬結果可知,非線性系數從γ=120W-1·Km-1到γ=110W-1·Km-1,從圖1a可發現輸出的SC譜線的寬度在不斷增加。從圖1c時域的傳輸波形可分析出拉曼響應隨時間延長。綜合圖1a、1c發現頻譜出現展寬,在脈沖前沿存在振蕩現象,主要是因為超短脈沖在光纖中產生SC譜受高階色散的影響嚴重,并且高階色散造成的影響是非對稱性的。
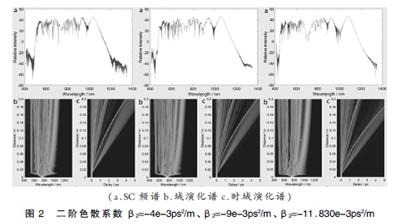
本文所模擬的皮秒脈沖寬度為t0=12.5ps,對于皮秒量級的寬度,二階色散對光纖色散占主要影響。在此處的模擬中,非線性系數確定為γ=120W-1·Km-1不變,光纖二階色散分別取值為β2=-4e-3ps2/m,β2=-3e-3ps2/m,β2=-11.830e-3ps2/m。結果如下:
分析模擬結果可知,二階色散取值從β2=-4e-3ps2/m到β2=-11.830e-3ps2/m,圖2a中SC譜線的頻譜寬度沒有明顯增加,平坦性有明顯上升的趨勢。分析圖2c時域演化譜,隨著二階色散取值的增加,時域延時也隨之增大。在二階色散取值為β2=-4e-3ps2/m時,自相位調制對展寬起主要作用。在二階色散取值為β2=-11.830e-3ps2/m時,色散效應與自相位調制競爭,抑制了頻率啁啾,使譜線的平坦度更好。
在藍寶石光纖中產生超連續譜過程中,還需要考慮光纖長度對非線性效應的影響,光纖的色散長度被定義為:
光纖的非線性長度被定義為:
上式中t為輸入脈沖寬度,β2為光纖的二階色散,γ和P0分別為光纖非線性系數和輸入脈沖峰值功率。
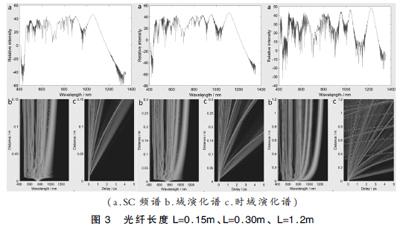
代入模擬數值光纖色散長度LD約為3.38m,LNL約為0.011m。改變光纖長度數值L=0.15m,L=0.30m,L=1.2m時,輸出超連續譜的情況如下:
分析模擬結果可知,光纖長度的數值L=0.15m增加到L=0.30m,分析圖3a圖3b可發現連續譜有展寬的趨勢。當光纖長度的數值L=1.2m時展寬程度反而降低。其原因是皮秒脈沖在藍寶石光纖中傳輸的距離較短時,其非線性效應主要是自相位調制作用,自相位調制作用造成脈沖頻譜對稱展寬。當皮秒脈沖在藍寶石光纖中的傳輸距離増加,會產生很多新的頻率,此時拉曼散射就會占主要作用,脈沖頻譜向長波長方向展寬。所以繼續增長光纖不會使頻譜繼續展寬。
3 結論
采用分步傅里葉方法求解廣義非線性薛定諤方程,數值模擬在藍寶石光纖中產生超連續譜的過程,保持輸入的皮秒脈沖參數不變,對在不同參數藍寶石光纖中傳輸特性及演化過程進行分析,得到頻域演化圖、時域演化圖及SC輸出光譜。結果表明,增大藍石光纖的非線性系數,可以獲得更寬的輸出脈沖頻譜;增大藍寶石光纖的二階色散,輸出SC譜線的平坦性隨色散的增加有上升趨勢;當光纖的長度從0.15m增大到0.30m時,超連續譜的譜線有展寬的趨勢,但在光纖長度為1.2m時平坦度反而下降,其原因是皮秒脈沖在藍寶石光纖中產生非線性效應,在不同的傳輸距離起主導的非線性效應也不相同。此結論對選用合適的光纖參數,獲得較為理想的超連續譜的輸出具有重要的指導意義。
參考文獻
[1]Husakou A V , Herrmann J.Supercontinuum Generation of Higher-Order Solitons by Fission in Photonic Crystal Fibers[J]. Physical Review Letters, 2001, 87(20):203901.
[2]Govind P Agrawal. Nonlinear Fiber Optics[J]. Lecture Notes in Physics, 2001, 18(1).
[3] Chen J B , Qin M Z , Tang Y F.Symplectic and multi-symplectic methods for the nonlinear Schr?dinger equation[J]. Computers & Mathematics with Applications, 2002, 43(8-9):1095-1106.
[4] Liu X , Lee B.A fast method for nonlinear Schrodinger equation[J]. IEEE Photonics Technology Letters, 2003, 15(11):1549-1551.
[5] Premaratne M.Analytical characterization of optical power and noise figure of forward pumped Raman amplifiers.[J]. Optics Express, 2004, 12(18):4235-45.
[6] Amans D , Brainis E , Haelterman M , et al. Vector modulation instability induced by vacuum fluctuations in highly birefringent fibers in the anomalous-dispersion regime[J]. Optics Letters, 2005, 30(9):1051-1053.
[7]Rockmore, Daniel N.Recent progress and applications in group FFTs[J]. 2003.
[8] Karen Marie Hilligs?e, Henrik N?rgaard Paulsen, Jan Th?gersen, et al. Initial steps of supercontinuum generation in photonic crystal fibers[J]. Journal of the Optical Society of America B, 2003, 20(9):1887-1893.
[9] Lin S S , Hwang S K , Liu J M.Supercontinuum generation in highly nonlinear fibers using amplified noise-like optical pulses[J]. Optics Express, 2014, 22(4):4152.
[10] Agrawal G P.Ultrashort Pulse Propagation in Nonlinear Dispersive Fibers[J]. 2016.
[11] Zhu Z , Brown T G.Experimental studies of polarization properties of supercontinua generated in a birefringent photonic crystal fiber[J]. Optics Express, 2004, 12(5):791-796.

