地鐵隧道開挖引起地表沉降規律的有限元分析

袁方

（貴州工程應用技術學院土木建筑工程學院，貴州 畢節551700）

1 概述

目前，城市軌道交通在各大城市中得到快速的發展，隨著大量地鐵隧道工程的建設，對其臨近地表和建構筑物造成很大的破壞。地鐵隧道施工將引起周圍地層應力和位移場產生變化，使周圍土體發生壓縮、剪切、變形、松弛等復雜變化，從而引起地表發生大范圍不均勻沉降，致使周圍建筑物發生開裂、傾斜及倒塌，因此研究地鐵隧道開挖引起的地表沉降規律具有重要的現實意義。根據地表沉降實測數據，Maros[1]首次提出隧道開挖所引起的地表沉降符合高斯正態分布。其后，Peck[2]等學者相繼證明了隧道開挖所引起的地表沉降也符合高斯正態分布，并給出了相應的計算公式。段紹偉[3]在隧道施工中結合現場地表下沉實測數據，對Peck 公式進行修正，得到適用于相應實際工程的隧道開挖引起的地表沉降計算公式。徐干成[4]結合實際工程，采用數值模擬的手段，分析了不同的隧道施工方式、地質條件、支護情況的變化對地表沉降的影響。但大多數研究多集中在隧道開挖引起的地表橫向沉降規律的研究，對于隧道開挖過程中，地表隨著隧道開挖步推進的縱向動態沉降規律研究較少。因此本文通過有限元數值分析方法建立地鐵隧道施工的三維模型，選取合適的開挖步，模擬隧道開挖這一動態過程對地表沉降規律的影響。

2 有限元分析模型建立

2.1 工程概況

本文以某地鐵2 號線某區間段作為研究對象，此區間段的地層參數和襯砌支護參數如表1 所示；地鐵隧道位于礫質粘性土內，開挖半徑為3.2m，埋深為20m，如圖1 所示。

2.2 三維計算模型

為便于有限元模型的建立，本文在已有研究的基礎上，作出如下基本假定：（1）假定土體為均勻、各向同性的彈塑性體，土體塑性屈服滿足D-P 材料模型的Von Mises 屈服準則；（2）假定地表和土層均為水平層狀分布，不考慮相鄰土層之間的凹凸情況；（3）有限元建模時不考慮地下水的影響。在有限元建模時，為了消除模型邊界約束條件的影響，取有限元模型的長邊長為隧道開挖直徑的8 倍，短邊長為隧道開挖直徑的6 倍，上邊界取至地表表面，下邊界取至距離隧道底部向下3 倍隧道開挖直徑處；根據隧道開挖半徑取三維有限元模型的長度為48m，寬度為48m；根據隧道的實際位置，取強風化土以上的三層土體作為研究對象，三維有限元模型的高度取為43m，隧道埋深根據實際工況取為20m。三維有限元模型的邊界約束條件根據土體實際擾動情況進行設置，對土體下邊界進行豎向位移約束；上邊界為地表面，設置為自由邊界條件；考慮到隧道在施工過程中土體僅在自重作用下產生豎向位移，故對有限元模型左右邊界施加水平位移約束。

表1 地層參數和襯砌支護參數[5]

圖1 地層立面圖[5]

圖2 中間斷面圖

圖3 隧道開挖示意圖

2.3 土體及襯砌支護的模擬

本文采用8 節點實體單元來模擬土體，土體的彈塑性本構采用D-P 材料模型，土體參數選取見表1，根據實際分層情況選取，再通過D-P 材料模型的等效應力計算公式進行換算得到相應的參數。襯砌支護采用4 節點殼單元來模擬，不考慮襯砌支護在正常使用過程中進入塑性階段，建模時將其視為線彈性模型，支護參數選取見表1。

2.4 地鐵隧道開挖模擬

在模擬隧道開挖前，需采取對土體進行地應力平衡的方式來消除土體在自重荷載作用下產生的固結變形；ABAQUS 模擬地應力的平衡有多種，由于本文研究隧道上部沒有其他結構，因此采用ABAQUS自動地應力平衡的方法來模擬地應力平衡，從而達到消除土體前期固結變形的效果。有限元模擬隧道施工過程的本質是相關單元體剛度及荷載的遷移和恢復，本文采用生死單元法來模擬隧道每一個開挖步的推進過程。隧道開挖步的長度取為2m，由于有限元模型沿著隧道開挖方向的長度為48m，故分為24 步對隧道進行模擬開挖，中間斷面圖及隧道開挖示意圖如圖2、圖3 所示。

3 地表沉降的數值計算結果分析

3.1 橫向地表沉降的分析

沿著隧道縱向開挖方向，取中間斷面作為目標斷面，以未發生沉降時的地表為0 點，地表在隧道開挖完成后向上隆起為正，向下產生沉降為負。提取目標斷面在隧道所有開挖步完成后的地表沉降規律如圖4 所示。從圖中可以看出，隧道開挖完成后的地表沉降規律呈反正態分布的曲線形式，地表最大沉降值為22.5mm，在線路中心處產生，并隨著距線路中心的距離增大，地表沉降值逐漸減小，最終在距離線路中心25m左右的位置減小為零；從圖中沉降曲線的斜率可以看出，地表沉降曲線的斜率隨著遠離線路中心逐漸減小，地表沉降曲線的斜率在距離線路中心0m 到5m 的范圍內相比于在距離線路中心5m 到25m 的范圍內較大，說明地表沉降在距離線路中心0m 到5m 的范圍內受隧道開挖的影響較大；故可得到如下結論：地表在接近隧道開挖的范圍內，受隧道開挖的影響較大，在遠離隧道開挖的范圍時，受隧道開挖影響較小（如圖4-5）。

3.2 縱向地表沉降的分析

本研究在模擬隧道開挖時分為24 步對隧道進行開挖，得到起始開挖斷面、中間目標斷面和最終斷面的線路中心點的沉降值隨著隧道開挖步推進的變化規律如圖5 所示。從圖中可以看出，三個不同斷面線路中心點的沉降值均隨著隧道開挖步的推進而增大，在隧道24 個開挖步完成后，三個斷面線路中心的沉降值達到最大，其值約為22.5mm。從沉降曲線斜率變化趨勢可以看出，三個不同斷面線路中心點隨隧道開挖推進的沉降曲線斜率變化趨勢各有不同，最終斷面線路中心點沉降曲線的斜率隨著隧道開挖步的推進而增大；目標斷面線路中心點沉降曲線的斜率隨著隧道開挖步的推進先增大后減小，且斜率的最大值位于隧道第12 開挖步完成后；起始斷面線路中心點沉降曲線的斜率隨著隧道開挖步的推進而減小；說明地鐵隧道開挖接近某一斷面時，對該斷面地表的沉降影響逐漸增大，當開挖遠離該斷面時，對該斷面地表的沉降影響逐漸減小，且在開挖推進到該斷面時，對該斷面地表的沉降影響最大。選取隧道第12 個開挖步完成后及隧道第24 個開挖步完成后的地表沉降云圖如圖6、圖7 所示。從圖6 可以看出，隨著隧道開挖步向前推進，隧道上方的土體會發生沉降，下方的土體會發生隆起，在橫向斷面上，隨著距隧道線路中心距離的增大，下沉值和隆起值均逐漸減小；地表最大沉降值發生在第一個開挖步的正上方，沿著隧道開挖步推進的方向，地表沉降值逐漸減小。對比圖中不同開挖步完成后的地表沉降云圖可知，隨著地鐵隧道開挖步向前推進，在起始開挖斷面上方，地表先形成一個沉降槽，隨著開挖推進，沉降槽逐漸擴大，最終在隧道所有開挖步完成后趨于穩定（圖6-7）。

圖4 地表沉降模擬值

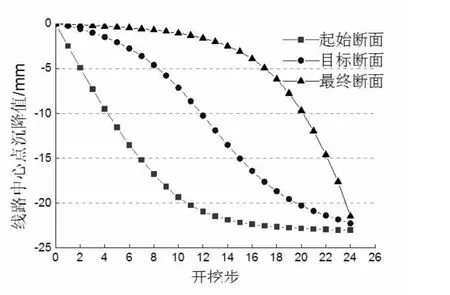
圖5 不同斷面隨隧道開挖推進的沉降值

圖6 第12 個開挖步完后地表沉降云圖

圖7 第24 個開挖步完后地表沉降云圖

4 結論

本文以某地鐵2 號線某區間段作為研究對象，通過有限元數值分析方法模擬了隧道開挖對地表沉降規律的影響，得出如下的結論：

4.1 地表橫向沉降規律呈反正態分布的曲線形式，地表在線路中心處產生最大沉降，并隨著距線路中心的距離增大而逐漸減小。地表在接近隧道開挖的范圍內，受隧道開挖的影響較大，在遠離隧道開挖的范圍時，受隧道開挖影響較小。

4.2 沿著隧道的縱向，地鐵隧道開挖接近某一斷面時，對該斷面地表的沉降影響逐漸增大，當開挖遠離該斷面時，對該斷面地表的沉降影響逐漸減小，且在開挖推進到該斷面時，對該斷面地表的沉降影響最大。

4.3 隨著地鐵隧道開挖步向前推進，在起始開挖斷面上方，地表先形成一個沉降槽，并隨著開挖推進，沉降槽逐漸擴大，最終在隧道所有開挖步完成后趨于穩定。