基于遺傳算法的煤炭港口泊位分配優化模型

李曉玲

（北京交通大學海濱學院 基礎教學部，河北 黃驊 061199）

1 引言

煤炭作為我國的主要能源，是我國經濟飛速發展的重要支撐[1]。在我國“西煤東運，北煤南下”的戰略下，煤炭港口發揮了重要作用。近年來，隨著經濟的發展，港口的吞吐量不斷提升，給港口帶來巨大經濟效益的同時也帶來了很多挑戰。畢竟港口資源是有限的，如何合理有效的利用港口資源實現更大的吞吐量，成為了港口所面臨的重大問題。泊位資源作為煤炭港口的稀缺資源，其合理分配不僅能夠提升裝船效率，從而減少船舶在港時間，還能夠為后續生產計劃環節的實施和優化奠定基礎。但是，由于煤炭種類繁多，煤炭港口不同于集裝箱港口，目前的調度主要還是人工調度，因此對煤炭港口的智能調度研究對提高港口的資源利用率，緩解疏港壓力，增加港口效益有著重要的理論和現實意義。

目前，國內外專家都對港口的資源調度問題做了大量深入的研究。Imai 等[2]以最小化船舶等待時間為目標，模擬了靜、動態分配模型，采用拉格朗日松弛法對模型進行求解。Henesey 等[3]采用Agent 技術對集裝箱港口的船舶運輸策略進行了仿真實驗，并對不同的策略進行了比較和評價。Wang 和Lim[4]將NP泊位分配問題轉化成了一個多階段決策程序，利用隨機定向搜索算法，提出了改善定向搜索計劃、兩階段節點質量評估、隨機節點選擇標準。韓駿等[5]提出了集裝箱碼頭的泊位與岸橋聯合調度問題的協調調度優化模型。王軍等[6]采用動態學習方法對在泊時間計算函數進行更新，再基于所得函數對泊位調度方案進行優化，設計了并行算法。劉強等[7]對基于線性規劃的煤炭碼頭泊位調度問題進行研究，建立了以船舶整體缺煤量最少和整體在泊時間最短為目標的逐級線性規劃模型。綜合國內外對港口泊位調度問題的研究發現，大部分的泊位調度問題研究主要集中在集裝箱碼頭，對于煤炭碼頭的泊位調度問題研究很少。

本文以某大型輸出型煤炭港口系統為背景，充分研究了輸出型煤炭港口的服務系統特征，在考慮場存能力的前提下，以船舶在港總時間最短及整體裝煤量最大為目標建立數學模型，并利用改進的遺傳算法對模型進行求解。

2 問題模型

2.1 問題描述

泊位調度問題就是研究一個計劃周期內的到港船舶在什么時候進入到什么位置的泊位問題。在煤炭港口物流系統中，船舶作業流程如圖1 所示，當船舶到達錨地時，工作人員根據貨量需求信息和堆場存儲信息，結合碼頭正在進行的工作信息，為船舶指定合適的堆場位置及泊位，發送作業指令給各工作單元和裝卸設備，進行裝貨作業。裝貨完成后，船舶離港。

堆場是用來儲存煤炭的場所，由于地理空間及設備的限制，每個垛位堆放的基礎原煤只能被運輸到可到達的若干泊位上。客戶需求的煤種稱為合同煤種，合同煤種可以由不同種類的基礎原煤按照一定的比例混合而成，這個過程稱為配煤，配煤過程中需要的基礎原煤種類和比例稱為配煤方案，對于一艘船舶的一種合同煤種,可以有多個配煤方案供其選擇。

正是因為煤炭港口的這個特性，所以在為船舶指泊時，不僅要考慮船泊匹配約束、時間約束、設備約束等，還要考慮船貨匹配約束。由于合同煤種可能有多個配煤方案供其選擇，所以待排船中有可能存在某些船舶共享幾種原煤的情況，若煤量場存不足，就有可能出現排在前面的船取走煤后，后面的船舶就只能等貨的情況，這不僅造成對泊位資源的浪費，也降低了港口的吞吐量。

為此，在煤量場存不足的條件下，本文建立了以港口總輸出煤量最大及船舶總在港時間最小為目標的多目標線性規劃模型，并給出基于遺傳算法的求解方法。

圖1 船舶作業流程圖

2.2 模型假設

為便于模型建立，首先做如下假設：

（1）不考慮機械故障、天氣因素等干擾。

（2）假設堆場在該規劃期內不會補充庫存。

（3）假設船舶一旦停泊不允許移泊。

（4）假設船舶進港后先在錨地等候，一旦被安排進泊便開始作業。

（5）假設每條船舶符合其船型約束的可停靠泊位提前已知。

（6）假設機械的作業效率是一個固定值d。

（7）假設船舶在航道上行駛的時間忽略不計，船舶在每個泊位上的工作時間，即在泊時間窗可以提前計算得出。

2.3 符號說明

b：泊位編號，b ∈B。

v：一個計劃周期內的在港船舶編號,v ∈V。

Vb：符合泊位b船型約束的船舶集合，Vb?V。

Av：船舶v的計劃到港時間。

Gvbk：船舶v停靠在泊位b上作為第k條船被服務時泊位b可到達的堆場可以為其提供的煤量。

Lv：船舶v所要求的配載煤量。

η:船舶要求的最小匹配度。

xvbk=1 表示船舶v停靠在泊位b上作為第k條船被服務，否則，取0。

Cvbk：船舶v停靠在泊位b上作為第k條船被服務時對應的裝載量。

2.4 模型建立

港口企業的利潤取決于港口的整體輸出量，由于存在爭煤現象，整體輸出量一方面取決于港口的效率，主要表現在船舶的總在港時間，一方面取決于船舶的整體裝載量，故本文以整體裝載量最大和總在港時間最小為目標函數，考慮船舶與泊位的一次性服務約束、船舶的裝載量約束以及時間窗約束，建立如下模型。

目標函數：

式（1）表示所有船舶的整體裝載量最大，式（2）表示所有船舶的總在港時間最小。

約束條件：

一次性服務約束：

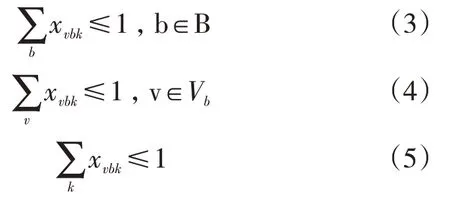
式（3）表示一艘船只能停靠在一個泊位上，b表示泊位編號，B表示所有泊位的集合；式（4）表示一個泊位一次性最多只能服務于一條船，Vb表示符合泊位b船型約束的船舶集合；式（5）表示在整個計劃周期內一條船最多被服務一次。

裝載量約束：

式（6）、（7）限制了船舶v停靠在泊位b上作為第k條船被服務時對應的裝載量不得小于船舶要求的最小匹配量，也不可能大于相應堆場可以為其提供的煤量。

時間約束：

式（8）-（10）表示第k條船必須在前一條船離泊之后進泊，且計劃進泊時間必須大于計劃到港時間，小于計劃離泊時間。

3 基于改進遺傳算法的模型求解方案

該問題是一個具有復雜的多約束條件、多目標函數的優化問題，很難找到精確的算法。遺傳算法是模擬自然界生物進化機制的一種算法，具有很好的自組織性、自適應性和自學習性，但傳統的遺傳算法在實際應用中容易陷入局部最優，或者求解結果與實際情況不一致，為本文在求解模型時加入人工干預的啟發式規則，以提高求解的高效性和有效性。

3.1 染色體編碼

遺傳算法最常用的編碼方式是二進制編碼，但是泊位調度問題的特性決定了使用二進制編碼計算機不易處理，因此本文采用泊位-次序的二維編碼方式。例如，一個周期內的到港船舶有9 只，可用泊位有3個，則我們將橫軸劃分為9個區間，豎軸劃分為3個區間，得到一個3×9 的矩陣，矩陣中第i行第j列的值為船舶序號，記做vij，表示第vij號船在第i個泊位作為第j條船被服務。圖2則表示一個染色體，第2 行第4 列的元素3 表示3 號船舶停靠在2 號泊位上被第4 個服務，在它前面接受服務的船舶依次是7號、9號、2號船。

圖2 染色體舉例

這里的0表示不再排船，要求每一行的第一個零元素后不再出現非零元素。

3.2 適應度函數

本文所建立的模型為雙目標函數模型，由于兩個目標的量綱不同，根據問題本身特性，選擇排序方式[8]來計算個體的適應度。

對每一個個體xi，分別計算其兩個目標函數值，根據計算的值對所有個體進行排序，得到排序序列S1={R1(xi)}；S2={R2(xi)}，其中，Rj(xi)(j=1,2)表示個體xi在目標j中的優劣排列序號，取值越小說明該個體對于該目標越優。設種群規模為N，定義以下公式作為個體的適應度。

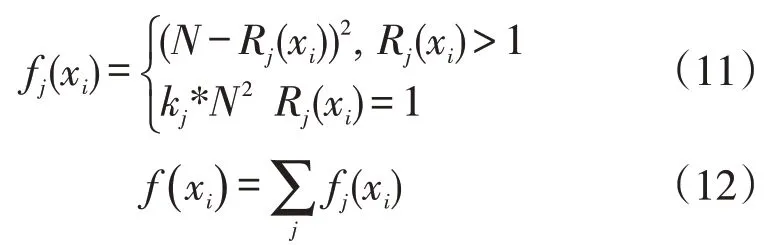
式（11）定義了個體對每個目標的適應度值，分段的意義在于使得最優解的適應度值足夠大。式（12）則表示個體的總適應度值。

3.3 初始種群

種群初始化過程結合隨機生成和啟發式規則的混合方式。啟發式規則包括先到先服務（FCFS）原則、緊急船優先、自有船優先等原則，對產生的隨機個體驗證是否滿足約束條件，進行初步篩選，這里涉及到的主要問題為泊位指定和順序指定（即時間指定）。具體操作過程為：

第一步：根據船貨匹配、船泊匹配條件及設備可達性等，確定可用泊位集，隨機選擇泊位；

第二步：計算可靠泊時間約束，如果該泊位已經有船，隨機選擇排列順序，否則根據最早可靠泊時間窗，隨機選擇時間點，作為該泊位第一艘被服務船舶；若可靠泊時間約束無解，重新制定泊位，若所有泊位無解，則計入未排船集合。

第三步：更新數據。將啟發式規則和隨機生成原則結合在一起，既保證了初始種群中基因的多樣性，又保證初始種群的優良性和有效性。

3.4 遺傳操作

遺傳操作主要包括選擇、交叉和變異操作。

（1）選擇操作。選擇操作的目的是為了從群體中選擇優良的個體，使他們有機會作為父代來繁殖子孫。根據適應度函數的特性，這里選用輪盤賭方法。

第一步，根據適應度函數的定義方式，計算出每一個個體的適應度值；

第四步：若r ＜q1，則選擇個體1，否則選擇個體k，使得qk-1＜r ≤qk成立；

第五步：重復第三、四步N次。

（2）交叉操作與變異操作。由適應度函數的特性，交叉概率和變異概率都由以下公式自適應產生。

其中fmax為群體中所有個體的最大適應度值，為平均適應度值為要進行交叉的個體的最大適應度值（要進行變異的個體的適應度值），c,d為[ ]0,1之間的常數。由于采用二維編碼方式，這里舉例說明具體的交叉方式和變異方式。

①選擇一對個體作為父代個體1 和父代個體2，如圖3所示。

②生成隨機數P與交叉概率pc比較，如果P ＞pc，則不進行交叉，直接將父代復制到子代中，否則轉③。

③隨機選擇一個位置，寫出對應元素對。如果沒有零元素，如第2 行第3 列，對應元素對為（2，4），找到個體2中該位置船號（4）在個體1中的位置（第3行第1列），交換這兩個位置上的船號；同時找到個體1 中該位置船號（2）在個體2 中的位置（第1 行第1列），交換這兩個位置上的船號，得到新一代個體（如圖4所示新個體1、新個體2），否則，轉④。

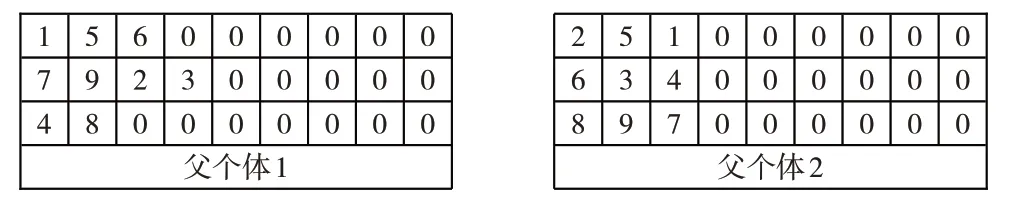
圖3 父個體舉例

④若有兩個零則不進行交叉操作，否則若有一個零如第2行第4列（3,0），則從該非零數字所在的個體中任選一行的第一個零與之互換（若該非零數字為所在行最后一個非零數字，則與除了本行外的其他行的非零數字互換），從零元素所在的個體中找到該非零數字，二者交換。剔除非零行非零數字前面的零，產生新一代個體（如圖4所示新個體3、新個體4）。

圖4 新個體舉例

⑤對于通過選擇復制及交叉產生的新個體進行變異操作，由于變異概率pm比較小，變異操作一般不發生，變異操作采取單點變異方式。對個體中的每一個基因，產生一個隨機數p，如果p ＞pm則不發生變異，否則隨機產生一個位置，將該位置的基因與此基因進行交換，如果隨機產生的位置與該基因位置相同，則不交換。

4 試驗與仿真

算例以某港口實際數據庫為依據，計劃周期為48小時，計劃周期內的到港船舶為26艘，最小匹配度設置為0.8。通過MatlabR2012a 實現，得到結果。與其人工調動數據做對比，見表1。

表1 人工調度與模型調度數據表

與人工調度相比，雖然本文所建模型調度使未排船量增加了，但是船舶的平均等待時間減少了34%，總裝載量提高了2.5%，達到了優化的目的。