考慮延期成本承諾交貨時(shí)間與產(chǎn)能擴(kuò)張決策

謝祥添

（廣東金融學(xué)院 科技金融重點(diǎn)實(shí)驗(yàn)室，廣東 廣州 510521）

1 引言

Stalk J G[1]提出時(shí)間將成為企業(yè)獲得競(jìng)爭(zhēng)優(yōu)勢(shì)的下一個(gè)資源。當(dāng)前，時(shí)間已經(jīng)與價(jià)格一樣成為企業(yè)在市場(chǎng)競(jìng)爭(zhēng)中獲得優(yōu)勢(shì)的因素之一。So K C 等[2]認(rèn)為企業(yè)以時(shí)間作為武器吸引客戶有三種策略：（1）快速服務(wù)；（2）提前預(yù)約；（3）承諾交貨時(shí)間。其中，訂單式生產(chǎn)企業(yè)多采用第三種策略。相對(duì)另外兩種策略，承諾一個(gè)統(tǒng)一的交貨時(shí)間較為有效[3]。由于受內(nèi)（如設(shè)備故障、人員流動(dòng)等）外（如需求、原材料供應(yīng)等）多種不確定因素的影響，企業(yè)難以實(shí)現(xiàn)100%按時(shí)交貨[4]。為此，部分企業(yè)承諾若不能按時(shí)交貨，則給予一定的賠償。如EMS承諾因自身原因造成郵件時(shí)限延誤的，可退還已收取的郵件資費(fèi)。Slotnick S A等[5]提及飛機(jī)零部件供應(yīng)商延期交貨賠償幾百萬美元。Ho T H 等[6]提出企業(yè)既能承諾一個(gè)較短的交貨時(shí)間，又能保證交貨時(shí)間的可靠性（即按時(shí)交貨的概率，部分文獻(xiàn)稱之為服務(wù)水平），就能吸引對(duì)時(shí)間敏感的客戶。那么，承諾多長(zhǎng)的交貨時(shí)間一方面能吸引客戶，另一方面又不會(huì)導(dǎo)致延期交貨頻繁從而付出過多的延期成本？

因此，考慮延期成本與承諾交貨時(shí)間的決策成為學(xué)者研究的焦點(diǎn)。較早對(duì)此研究的是Seidmann A等[7]，他們建立以時(shí)間總成本（包括交貨時(shí)間成本、延期成本和提前交貨成本）為目標(biāo)函數(shù)，以承諾交貨時(shí)間為決策變量的模型，證明了實(shí)際交貨時(shí)間服從任意隨機(jī)分布，存在最優(yōu)承諾交貨時(shí)間使目標(biāo)函數(shù)最小化。隨后，Grout J R 等[4]考慮延期成本和提前交貨成本研究供應(yīng)鏈交貨時(shí)間問題，證明了100%按時(shí)交貨是奢望；同時(shí)，他們還提出了實(shí)際交貨時(shí)間分別服從均勻分布、指數(shù)分布和三角分布時(shí)交貨時(shí)間成本最小化的條件。Hill A V 等[8]考慮延期成本，建立了以企業(yè)利潤(rùn)為目標(biāo)函數(shù)，以承諾交貨時(shí)間為決策變量的模型，得到了最優(yōu)承諾交貨時(shí)間數(shù)學(xué)表達(dá)式。該模型權(quán)衡了承諾交貨時(shí)間和延期成本的關(guān)系。最近部分學(xué)者研究了多階段生產(chǎn)的交貨時(shí)間問題。如Atan Z 等[9]研究了訂單驅(qū)動(dòng)的多階段裝配生產(chǎn)系統(tǒng)交貨時(shí)間決策問題，他們建立了以訂單總成本（包括提前交貨成本和延期成本）為目標(biāo)函數(shù)，以每一階段交貨時(shí)間為決策變量的模型，推導(dǎo)出多階段庫(kù)存成本和延期成本遞推方程，提出了一個(gè)求解多階段交貨時(shí)間的迭代啟發(fā)式算法。Jansen S 等[10]研究了由多個(gè)并行子組件階段和一個(gè)最終組裝階段組成的按訂單生產(chǎn)的交貨時(shí)間問題，他們考慮每個(gè)階段都有一個(gè)隨機(jī)的提前期，以及最終裝配階段延期產(chǎn)生罰款，建立以每個(gè)階段交貨時(shí)間為決策變量，以總期望成本最小化為目標(biāo)函數(shù)的模型，通過對(duì)模型的分析，得出了最優(yōu)交貨時(shí)間滿足報(bào)童過程。在我國(guó)，周穎[11]基于客戶價(jià)值，考慮延期成本，建立了客戶選擇行為的承諾交貨時(shí)間決策模型，證明了模型存在最優(yōu)承諾交貨時(shí)間使企業(yè)利潤(rùn)達(dá)到最大化和最優(yōu)承諾交貨時(shí)間長(zhǎng)于顧客期望的交貨時(shí)間。倪衛(wèi)濤等[12]考慮提前交貨產(chǎn)生倉(cāng)儲(chǔ)成本和延期交貨支付罰金，建立以訂單生產(chǎn)式企業(yè)單品收益為目標(biāo)函數(shù)，以承諾交貨時(shí)間為決策變量的模型，證明了模型存在最優(yōu)承諾交貨時(shí)間使企業(yè)邊際收益達(dá)到最大化。

以上主要從時(shí)間成本研究交貨時(shí)間的決策。然而，在需求一定的前提下，交貨時(shí)間隨著產(chǎn)能的增加而減少，隨著產(chǎn)能的減少而增加。所以有部分學(xué)者研究了承諾交貨時(shí)間和產(chǎn)能聯(lián)合決策問題。如，Nguyen T H 等[13]提出企業(yè)不僅要考慮客戶如何對(duì)交貨時(shí)間保證作出反應(yīng)，還要考慮其是否有足夠的產(chǎn)能履行承諾。因此，他們研究了企業(yè)利潤(rùn)與承諾交貨時(shí)間和產(chǎn)能的關(guān)系，得出了需求時(shí)間變化下最優(yōu)的承諾交貨時(shí)間和產(chǎn)能。謝祥添等[14]考慮需求具有數(shù)量和時(shí)間兩方面的不確定性，采用作業(yè)成本法建立以承諾交貨時(shí)間和產(chǎn)能為決策變量，以期望利潤(rùn)為目標(biāo)函數(shù)的模型，給出了最優(yōu)承諾交貨時(shí)間和最優(yōu)產(chǎn)能滿足的方程組，該研究表明結(jié)合生產(chǎn)過程和承諾交貨時(shí)間可靠性有助于提高產(chǎn)能的利用率和交貨時(shí)間的準(zhǔn)確性。Albana A S 等[15]考慮運(yùn)營(yíng)成本是時(shí)間敏感，分別建立了交貨時(shí)間決策模型、交貨時(shí)間與價(jià)格決策模型和交貨時(shí)間、價(jià)格和產(chǎn)能決策模型，給出了各個(gè)模型的最優(yōu)策略。以上文獻(xiàn)通過產(chǎn)能和交貨時(shí)間聯(lián)合決策得到了可靠性較高的交貨時(shí)間，因而忽略了延期成本，但是隨著時(shí)間競(jìng)爭(zhēng)的加劇，客戶對(duì)準(zhǔn)時(shí)交貨的重視，企業(yè)紛紛提出若不能按時(shí)交貨，承諾支付一定的賠償。因此，本文考慮延期交貨尾概率分布為指數(shù)分布，構(gòu)建了包含延期成本的承諾交貨時(shí)間和產(chǎn)能決策模型。

本文的貢獻(xiàn)在于考慮延期成本，以及產(chǎn)能與交貨時(shí)間的關(guān)系，建立以承諾交貨時(shí)間和產(chǎn)能為決策變量的模型，得到了聯(lián)合最優(yōu)的承諾交貨時(shí)間和產(chǎn)能擴(kuò)張。以此分析得出企業(yè)利潤(rùn)隨著承諾交貨時(shí)間或產(chǎn)能擴(kuò)張的增加先增加后減少，兩者相比，企業(yè)利潤(rùn)受承諾交貨時(shí)間影響更大。

2 模型的建立

2.1 模型參數(shù)及說明

r=單位收入，單價(jià)減去單位成本（除延期成本和產(chǎn)能成本外）；

c1=延期單位成本；

u=當(dāng)前產(chǎn)能，當(dāng)前生產(chǎn)系統(tǒng)可以生產(chǎn)的產(chǎn)品數(shù)；

z=產(chǎn)能擴(kuò)張，企業(yè)通過加班或增加臨時(shí)工等方式增加生產(chǎn)系統(tǒng)的產(chǎn)能；

c2=當(dāng)前產(chǎn)能單位成本；

c3=產(chǎn)能擴(kuò)張單位成本；

l=承諾交貨時(shí)間；

L=實(shí)際交貨時(shí)間；

P{L≤l}=實(shí)際交貨時(shí)間小于等于承諾交貨時(shí)間的概率。

2.2 需求函數(shù)

考慮客戶傾向于較短的交貨時(shí)間，建立承諾交貨時(shí)間需求函數(shù)：

式中，a 為b=0（需求與承諾交貨時(shí)間不敏感）時(shí)的需求（部分文獻(xiàn)稱之為潛在需求），b為需求承諾交貨時(shí)間敏感系數(shù)（b≥0）。承諾交貨時(shí)間需求函數(shù)有線性的，如 Wu Z 等[16]、Pekgun P 等[17]研究文獻(xiàn)的函數(shù)；也有非線性的，如 Hill A V 等[18]、Mallick R K 等[19]研究文獻(xiàn)的函數(shù)。

2.3 延期成本函數(shù)

眾多學(xué)者，如Kelton W D等[20]和Bratley P等[21]均指出實(shí)際交貨時(shí)間小于等于承諾交貨時(shí)間的尾概率分布為指數(shù)分布：

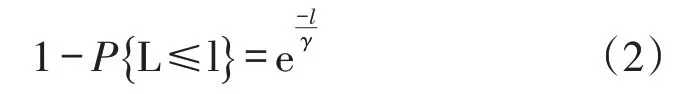
其中，γ為實(shí)際交貨時(shí)間均值。因?yàn)樵谛枨笠欢ǖ那疤嵯拢回洉r(shí)間受產(chǎn)能的影響：產(chǎn)能越大交貨時(shí)間越短，產(chǎn)能越小交貨時(shí)間越長(zhǎng)。所以產(chǎn)能與實(shí)際交貨時(shí)間均值γ 有減函數(shù)的關(guān)系[8]。在減函數(shù)關(guān)系中，我們假設(shè)它們成反比例的關(guān)系，構(gòu)建實(shí)際交貨時(shí)間均值γ關(guān)于產(chǎn)能的函數(shù)：

其中，θ為實(shí)際交貨時(shí)間均值γ與產(chǎn)能關(guān)系系數(shù)（θ＞0），其值可以通過統(tǒng)計(jì)分析（如回歸分析）確定。

因?yàn)檠悠诮回浉怕蔖{L＞l}=1-P{L≤l}，所以結(jié)合式（2）和式（3），可得關(guān)于產(chǎn)能和承諾交貨時(shí)間的延期交貨概率函數(shù)：

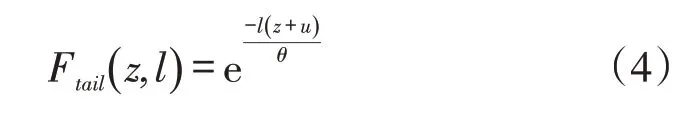
設(shè)u=50，θ=45。作產(chǎn)能擴(kuò)張z 分別為 0，15 和 50時(shí)的延期交貨概率，如圖1 所示。從圖1 可知，隨著產(chǎn)能擴(kuò)張的增大，延期交貨概率減小。

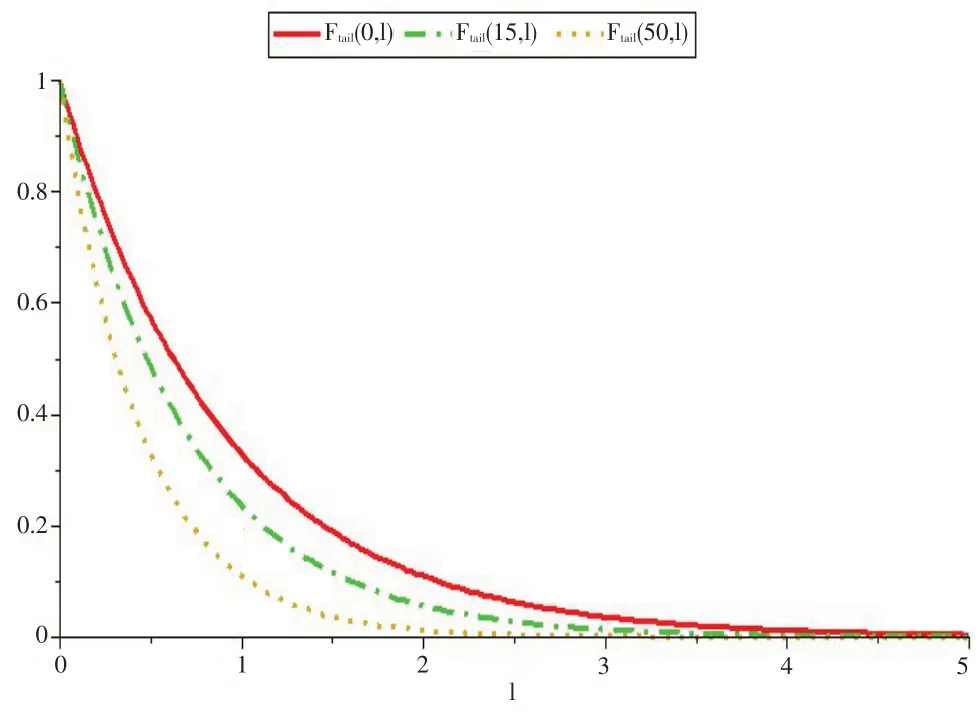
圖1 產(chǎn)能擴(kuò)張與延期交貨概率

根據(jù)式（1）和式（4），可得延期成本函數(shù)：

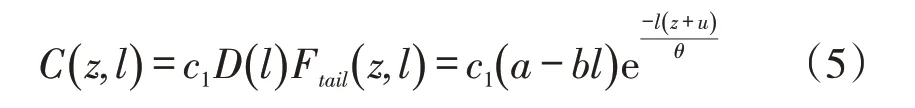
2.4 模型構(gòu)建

考慮延期成本，建立以企業(yè)利潤(rùn)為目標(biāo)函數(shù)，以承諾交貨時(shí)間和產(chǎn)能擴(kuò)張為決策變量的模型。

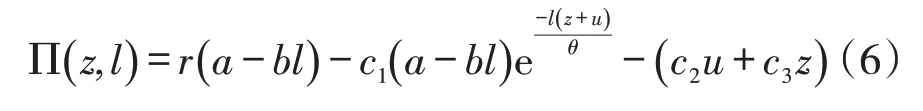
其中，第一項(xiàng)為收入；第二項(xiàng)為延期成本；第三項(xiàng)為產(chǎn)能成本。

3 模型分析

3.1 承諾交貨時(shí)間為決策變量

命題1 若僅以承諾交貨時(shí)間為決策變量，模型存在最優(yōu)承諾交貨時(shí)間，它的表達(dá)式為：

其中，LambertW(x)為歐米加函數(shù)或乘數(shù)對(duì)數(shù)[22]。

證明：式（6）對(duì)l 求一階偏導(dǎo)數(shù)，令其為零整理得：

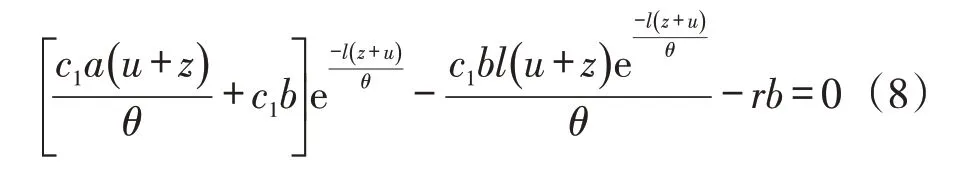
設(shè) t1=c1a(u+z)/θ+c1b，t2=c1b(u+z)/θ，t3=(u+z)/θ 和x=-lt3=-l(u+z)/θ，那么式（8）變換為：

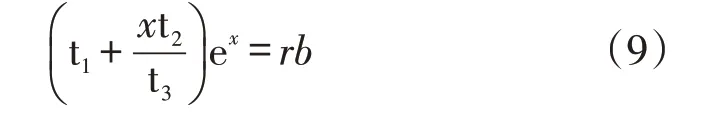
又設(shè)y=t1+xt2/t3,，這時(shí)式（9）變換為：

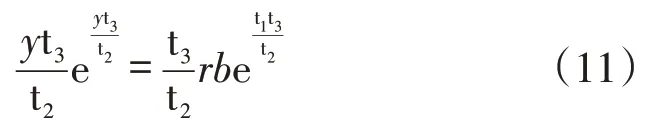
以yt3/t2作為未知數(shù)，求式(11)可得：

這時(shí)把y=t1+xt2/t3和x=-lt3代入式（12）化簡(jiǎn)得：

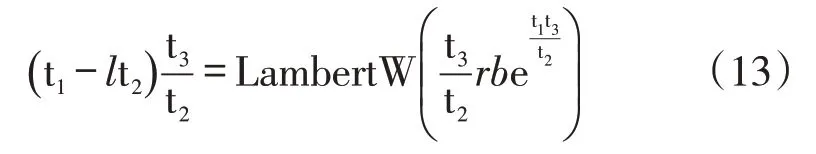
再把 t1=c1a(u+z)/θ+c1b，t2=c1b(u+z)/θ 和 t3=(u+z)/θ代入式（13）求解l，得：

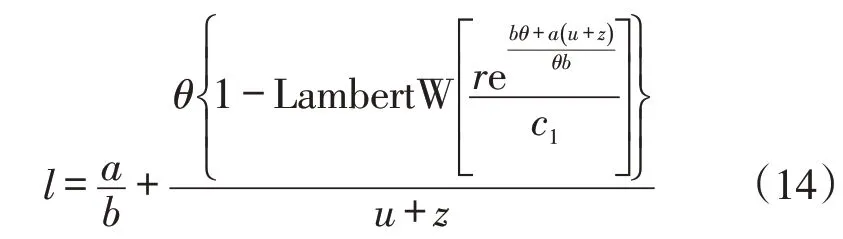
又因?yàn)槭剑?）對(duì)l求二階偏導(dǎo)數(shù)有：

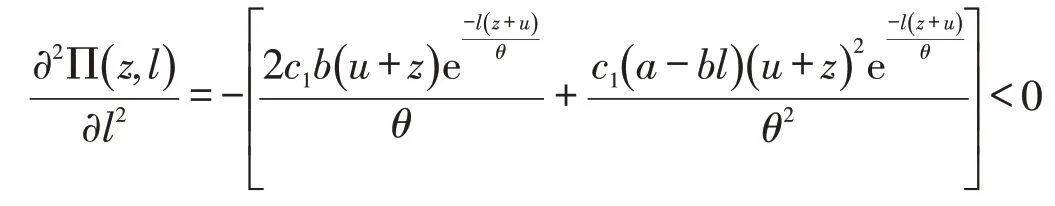
所以，式（6）關(guān)于l 存在最大值，最優(yōu)解為式（6）對(duì)l求一階偏導(dǎo)數(shù)為零的解，即式（14）。因此，命題1成立。

命題1結(jié)論：若不允許延期交貨（令c1=∞），這時(shí)有l(wèi)*=a/b+θ/(u+z)，這表明最優(yōu)承諾交貨時(shí)間隨著潛在需求a的增加而增加，隨著需求承諾交貨時(shí)間敏感系數(shù)b和產(chǎn)能擴(kuò)張z的增加而減少。所以企業(yè)在需大于供的市場(chǎng)中，承諾交貨時(shí)間較長(zhǎng)；在需求時(shí)間越敏感的市場(chǎng)中，承諾的交貨時(shí)間越短。承諾交貨時(shí)間與產(chǎn)能有減函數(shù)的關(guān)系。

3.2 產(chǎn)能為決策變量

命題2若僅以產(chǎn)能擴(kuò)張為決策變量，模型存在最優(yōu)產(chǎn)能擴(kuò)張，它的表達(dá)式為：

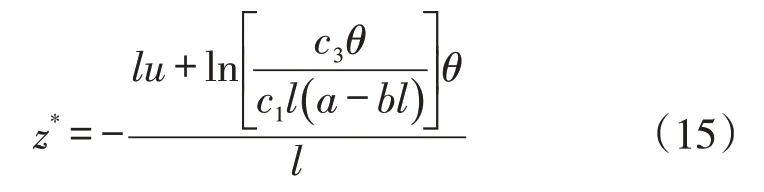
證明：式（6）對(duì)z求一階偏導(dǎo)數(shù)為零：

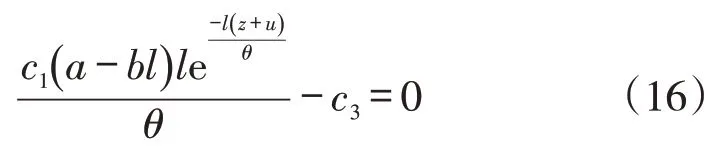
求解式（16）可得z的表達(dá)式：

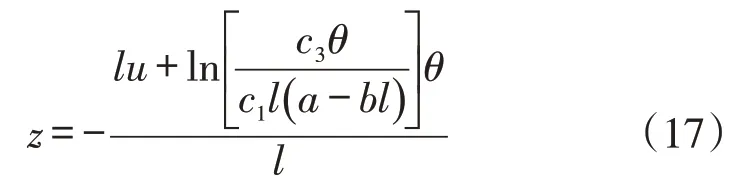
又因?yàn)槭剑?）對(duì)z求二階偏導(dǎo)數(shù)有：

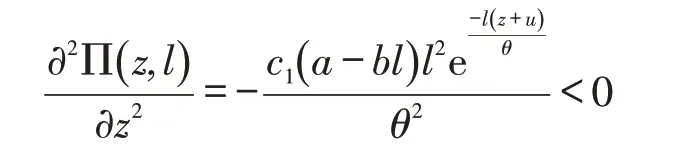
所以命題2成立。

命題2結(jié)論：由式（15）得：z*=-u-θln(c3θ)/l+θln[c1l(a-bl)]/l。這表明最優(yōu)產(chǎn)能擴(kuò)張隨著當(dāng)前產(chǎn)能u，產(chǎn)能擴(kuò)張單位成本c3和需求承諾交貨時(shí)間敏感系數(shù)b的增加而減少，隨著延期單位成本c1和潛在需求a增加而增加。同時(shí)易知，系統(tǒng)處于最優(yōu)狀態(tài)為產(chǎn)能擴(kuò)張為零時(shí)，即當(dāng)前產(chǎn)能滿足：u=-θln(c3θ)/l+θln[c1l(a-bl)]/l。

3.3 承諾交貨時(shí)間和產(chǎn)能為決策變量

（1）交替決策。企業(yè)在承諾交貨時(shí)間和產(chǎn)能決策前，一般存在著產(chǎn)能，這時(shí)產(chǎn)能擴(kuò)張為0，設(shè)z(0)=0。在z(0)前提下，企業(yè)可以根據(jù)式（7）確定最優(yōu)承諾交貨時(shí)間，設(shè)為l(0)*，這時(shí)企業(yè)得到第一次決策的最優(yōu)利潤(rùn)。接著，企業(yè)在l(0)*前提下，根據(jù)式（15）可得最優(yōu)產(chǎn)能擴(kuò)張，設(shè)為z(0)*，這時(shí)企業(yè)得到了第二次決策的最優(yōu)利潤(rùn)，如此反復(fù)。

當(dāng)然，企業(yè)也可以以當(dāng)前的承諾交貨時(shí)間作為初始承諾交貨時(shí)間，然后在初始承諾交貨時(shí)間條件下確定最優(yōu)產(chǎn)能擴(kuò)張。余下的決策過程與上述一致，略。

（2）同時(shí)決策

引理1 若(l0,z0)為式（6）的極值點(diǎn)，那它滿足以下方程組：

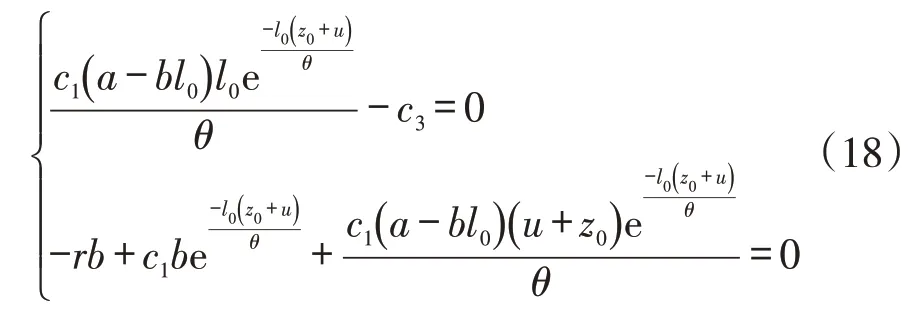
證明：設(shè)(l0,z0)為式（6）的極值點(diǎn)，把它代入式（6）分別對(duì)l 和z 求一階偏導(dǎo)數(shù)為零的方程組，可得式（18），所以引理1成立。

命題3 若存在極值點(diǎn)(l0,z0)使得式（19）成立，那么該極值點(diǎn)為極大值點(diǎn)。

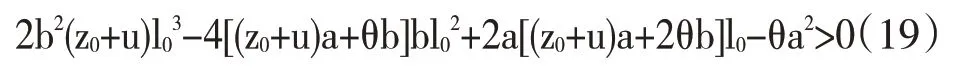
根據(jù)引理1可得極值點(diǎn)(l0,z0)，把極值點(diǎn)(l0,z0)分別代入A，B和C。根據(jù)極值點(diǎn)判斷公式有：

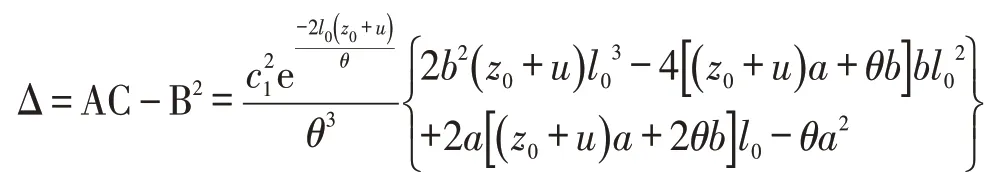
由式（19）可得Δ ＞0，又因?yàn)锳＜0，所以命題3成立。

命題3結(jié)論：模型不一定存在最優(yōu)的承諾交貨時(shí)間和產(chǎn)能擴(kuò)張；若存在，那么對(duì)所有有實(shí)際意義極大值點(diǎn)的函數(shù)值和邊界點(diǎn)(l*z=0,0)（把z=0代入式（7）可得l*z=0）的函數(shù)值進(jìn)行相互比較，其中最大者就是模型的最優(yōu)值，其對(duì)應(yīng)的點(diǎn)就是最優(yōu)的承諾交貨時(shí)間和產(chǎn)能擴(kuò)張。

4 數(shù)值實(shí)例

某衣服生產(chǎn)企業(yè)，其產(chǎn)品P 運(yùn)營(yíng)過程為：企業(yè)在網(wǎng)站發(fā)布產(chǎn)品P的信息（包括價(jià)格、交貨時(shí)間、定制流程等），客戶通過網(wǎng)站定制，企業(yè)根據(jù)客戶要求生產(chǎn)，生產(chǎn)完畢后交付。產(chǎn)品P采用網(wǎng)上定制式生產(chǎn)，出現(xiàn)了延期交貨頻繁的問題，因此需要確定合適的承諾交貨時(shí)間。

產(chǎn)品P根據(jù)歷史數(shù)據(jù)統(tǒng)計(jì)分析可知：其承諾交貨時(shí)間的尾概率分布近似服從指數(shù)分布，實(shí)際交貨時(shí)間均值與產(chǎn)能成反比例關(guān)系，關(guān)系系數(shù)為45，每天出售 1 000-10l 件，售價(jià)為 50 元/件，生產(chǎn)成本為 20 元/件，延期成本為10 元/件，產(chǎn)能為50 件/天，產(chǎn)能成本為10 元/件，通過加班、增加工人等方法增加產(chǎn)能的成本為12元/件。（1）求經(jīng)過3次產(chǎn)能擴(kuò)張（6次交替決策）后產(chǎn)品P最優(yōu)的承諾交貨時(shí)間和產(chǎn)能；（2）求產(chǎn)品P最優(yōu)的承諾交貨時(shí)間和產(chǎn)能。

依題意有 r=50-20=30 元/件，c1=10 元/件，c2=10元/件，c3=12 元/件，u=50 件/天，z(0)=0 件/天，θ=45，a=1 000件/天，b=10。

（1）經(jīng)過3次產(chǎn)能擴(kuò)張后產(chǎn)品P最優(yōu)的承諾交貨時(shí)間和產(chǎn)能

第一次決策：把 z(0)=0 件/天，r=30 元/件，c1=10 元/件，u=50 件/天，θ=45，a=1 000 件/天和 b=10 代入式（7）得：

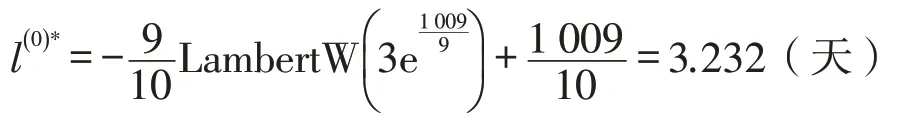
這時(shí)產(chǎn)品P的最優(yōu)利潤(rùn)為：2.826 4萬元/天。

第二次決策：把 l(0)*=3.232 天，c1=10 元/件，c3=12元/件，u=50件/天，θ=45，a=1 000件/天和b=10代入式（15）得：

這時(shí)產(chǎn)品P 的最優(yōu)利潤(rùn)為：2.828 5 萬元/天。余下決策過程見表1。

所以，經(jīng)過3次產(chǎn)能擴(kuò)張后，產(chǎn)品P的最優(yōu)承諾交貨時(shí)間為2.813 670 915天，最優(yōu)產(chǎn)能為62.769 405 20件/天，最優(yōu)利潤(rùn)為2.831 1萬元/天。

（2）產(chǎn)品P最優(yōu)的承諾交貨時(shí)間和產(chǎn)能

把r=30元/件，c1=10元/件，c3=12元/件，u=50件/天，θ=45，a=1 000件/天，b=10代入式（18）得：

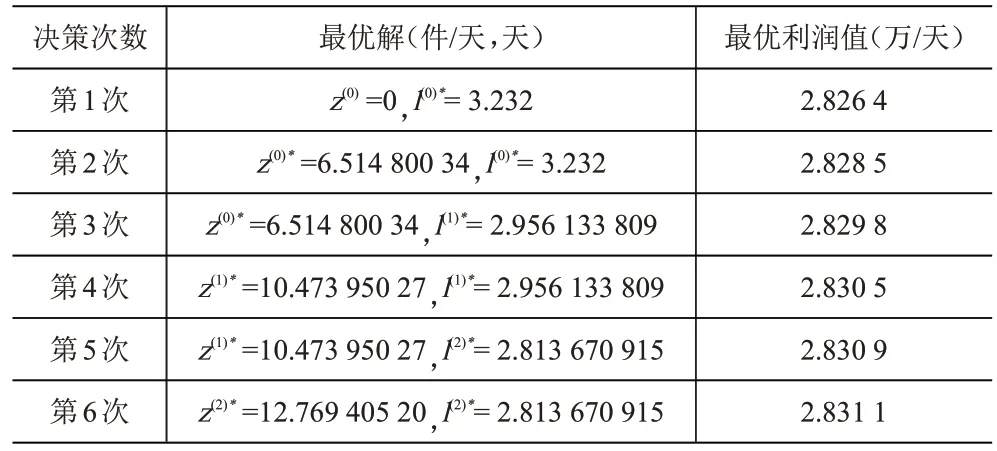
表1 最優(yōu)承諾交貨時(shí)間和產(chǎn)能決策

解上式得有實(shí)際意義的點(diǎn)為：{l0=2.647 000 263,z0=15.712 771 2}。把{l0=2.647 000 263,z0=15.71 2 771 2}代入式（19）有2.89×108＞0。所以{l0=2.647 000 263，z0=15.712 771 2}為極大值點(diǎn)，這時(shí)它對(duì)應(yīng)的函數(shù)值為2.831 3萬。因?yàn)閧l0=2.647 000 263,z0=15.712 771 2}極大值點(diǎn)對(duì)應(yīng)的值2.831 3大于邊界點(diǎn){l*z=0=3.232,z=0}對(duì)應(yīng)的值2.826 4。所以，產(chǎn)品P的最優(yōu)承諾交貨時(shí)間為2.647 000 263 天，最優(yōu)產(chǎn)能為 65.712 771 2 件/天，最優(yōu)利潤(rùn)為2.831 3萬元/天。

為了進(jìn)一步弄清利潤(rùn)和承諾交貨時(shí)間與產(chǎn)能擴(kuò)張的關(guān)系，令 r=30 元/件，c1=10 元/件，c2=10 元/件，c3=12元/件，u=50件/天，θ=45，a=1 000件/天，b=10。

首先，把上述r=30 元/件等代入式（6）作圖，如圖2 所示。從圖 2 可知，隨著 l 和 z 的增加，Π(z,l)是先增加后減少的曲面，這表明企業(yè)存在最大利潤(rùn)。

其次，把上述r=30元/件等，以及l(fā)0=2.647 000 263天代入式（6）作圖，如圖3所示。從圖3可知，隨著z的增加，Π(z,l)先增加后減少，當(dāng)Z達(dá)到15.712 771 2 件/天時(shí)，企業(yè)的利潤(rùn)最大。這說明企業(yè)初始增加產(chǎn)能縮短了交貨時(shí)間，使得需求增加得到的利潤(rùn)多于總成本（延期成本和產(chǎn)能成本）的增加，所以利潤(rùn)增加，當(dāng)產(chǎn)能擴(kuò)張超過最優(yōu)值后，需求增加帶來的利潤(rùn)小于總成本的增加，導(dǎo)致利潤(rùn)下降。

最后，把上述r=30元/件等，以及z0=15.712 771 2件/天代入式（6）作圖，如圖4所示。從圖4可知，隨著l的增加，Π(z,l)先快速增加后逐漸減少，當(dāng)達(dá)到2.647 000 263天時(shí)，企業(yè)的利潤(rùn)最大。這說明企業(yè)初始承諾交貨時(shí)間增加，延期成本節(jié)約比需求減少導(dǎo)致利潤(rùn)減少多，所以利潤(rùn)增加，當(dāng)承諾交貨時(shí)間超過最優(yōu)值后，則反之。同時(shí)，相對(duì)于z，Π(z,l)受到l的影響更加顯著。

圖2 利潤(rùn)和承諾交貨時(shí)間與產(chǎn)能擴(kuò)張的關(guān)系

圖3 利潤(rùn)和產(chǎn)能擴(kuò)張的關(guān)系

5 結(jié)束語

在需求一定的前提下，交貨時(shí)間主要受產(chǎn)能的影響，本文考慮延期成本以及產(chǎn)能與交貨時(shí)間的關(guān)系，構(gòu)建了延期成本函數(shù)，在此基礎(chǔ)上建立了以承諾交貨時(shí)間和產(chǎn)能為決策變量的模型。通過模型分析，得到了相互遞推的承諾交貨時(shí)間和產(chǎn)能擴(kuò)張關(guān)系式，在此基礎(chǔ)上，求解得到了最優(yōu)的承諾交貨時(shí)間和產(chǎn)能擴(kuò)張值。

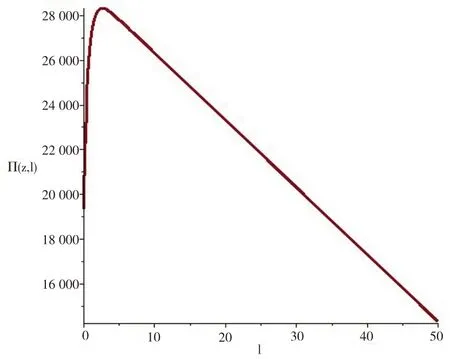
圖4 利潤(rùn)和承諾交貨時(shí)間的關(guān)系

模型不一定存在最優(yōu)的承諾交貨時(shí)間和產(chǎn)能擴(kuò)張值，若存在則可以根據(jù)命題3求得；若不存在，結(jié)合企業(yè)關(guān)于承諾交貨時(shí)間和產(chǎn)能的決策過程，采用交替決策方法可得適合企業(yè)自身情況的承諾交貨時(shí)間和產(chǎn)能。

最后，本文研究的延期成本僅考慮了企業(yè)是否按時(shí)交貨，如果企業(yè)不按時(shí)交貨則需要支付罰金。實(shí)際上，延期成本還會(huì)與延期時(shí)間長(zhǎng)度相關(guān)，這有待進(jìn)一步研究。