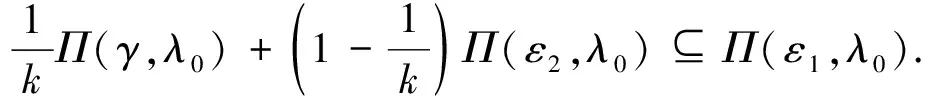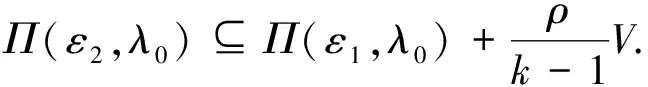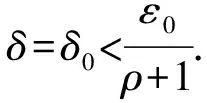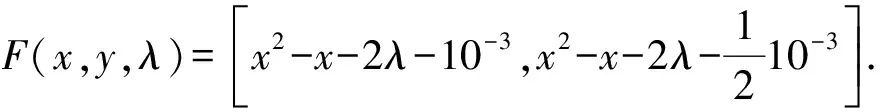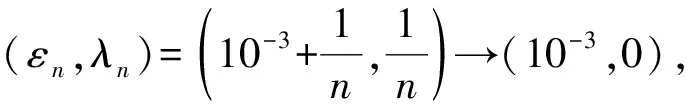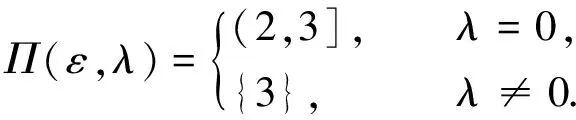集值向量均衡問題近似解映射的連續性

陳斌， 王浩智

(華僑大學 數學科學學院， 福建 泉州 362021)

均衡問題[1]為許多優化有關的重要問題提供了統一框架，如極值問題、變分不等式、互補問題、納什均衡、極大極小問題、不動點問題,以及交通網絡等.在過去的20年，均衡問題解及近似解的存在性條件已被廣泛研究[2-8].另一個重要的課題是研究均衡問題解及近似解的穩定性和敏感性分析.目前，有很多學者研究了解及近似解的(半)連續和H?lder連續性[9-15].為了獲得解或近似解的(半)連續性，許多文獻利用了映射的單調性或者解映射的信息.其中，映射的單調性可能導致整個解集是單點集.此外，假設條件中涉及解映射的信息是不合理的，在實踐中很難實現.當處理含參向量均衡問題解映射的(半)連續性時，許多文獻利用了標量化方法.然而，這一方法只有對含參弱向量均衡問題有效，對強向量均衡問題則不適用.文獻[16]在未使用標量化方法的情況下，建立了強向量均衡問題和對偶強向量均衡問題近似解映射的Hausdorff上下半連續性的充分條件，改進了已有文獻中的相關結果.

本文主要研究局部凸Hausdorff拓撲向量空間中擾動下的集值向量均衡問題的原問題和對偶問題，建立其近似解映射的Hausdorff上下半連續性的充分條件，改進和推廣了文獻[16]的已有結果.

1 預備知識

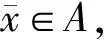
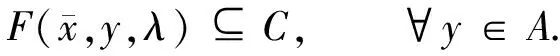
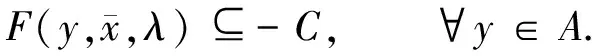
令e∈intC.對于(ε，λ)∈R+×Λ，設SVEP和DSVEP的ε-近似解集分別為

Π(ε，λ)={x∈A|F(x，y，λ)+εe?C，?y∈A}，

Πd(ε，λ)={x∈A|F(y，x，λ)+εe?-C，?y∈A}.

以下先給出一些基本概念和引理.

設F為X到Y的集值映射.

定義1[17]ⅰ) 若對于Y中任意滿足F(x0)?U的開子集U，都存在x0的一個鄰域N，使F(N)?U，則稱F在x0處上半連續.

ⅱ) 若Y中滿足F(x0)∩U≠?的任意開子集U，都存在一個x0的鄰域N，使得對于所有的x∈N，都有F(x)∩U≠?，則稱F在x0處下半連續.

ⅲ) 若F在x0處同時為上半連續和下半連續，則稱F在x0處連續.

引理1[18]F在x0處是下半連續的，當且僅當對于y0∈F(x0)及所有xα→x0，存在ya∈F(xα)，使得yα→y0.

定義2[18]ⅰ)F在x0處稱為Hausdorff上半連續，如果對于Y中原點的任意鄰域V，都存在x0的鄰域N，使得

F(x)?F(x0)+V， ?x∈N.

ⅱ)F在x0處稱為Hausdorff下半連續，如果對于Y中原點的任意鄰域V，都存在x0的鄰域N，則使得

F(x0)?F(x)+V， ?x∈N.

ⅲ) 如果F在x0處同時為Hausdorff上半連續和Hausdorff下半連續，則F在x0處稱為Hausdorff連續.

引理2[18]ⅰ) 如果F在x0處是上半連續，那么F在x0處是Hausdorff上半連續；反之，如果F在x0處是Hausdorff上半連續，且F(x0)是緊集，那么F在x0處是上半連續.

ⅱ) 如果F在x0處為Hausdorff下半連續，則F在x0處為下半連續；反之，如果F在x0處是下半連續，且F(x0)是緊集，那么F在x0處是Hausdorff下半連續.

定義3如果對于任意ε>0，存在λ0的鄰域N，使得對于所有x，y∈A和λ1，λ2∈N，都有

F(x，y，λ1)?F(x，y，λ2)+ε[-e，e]，

則稱集值映射F:A×A×Λ→2Y關于e∈intC在λ0處對于(x，y)∈A×A一致連續，其中,[-e，e]∶={x∈Y|x∈(e-C)∩(-e+C)}.

定義4[18]如果對于任意x1，x2∈A和t∈[0，1]，有

F(tx1+(1-t)x2)?tF(x1)+(1-t)F(x2)+C，

(1)

則稱映射F:X→2Y在凸集A?X上是C-凹的.

如果將式(1)替換為

F(tx1+(1-t)x2)?tF(x1)+(1+t)F(x2)-C，

則稱映射F:X→2Y在凸集A?X上是C-凸的.

對于固定的λ0∈Λ，可以得到以下結果.

引理3如果對于任意y∈A，F(·，y，λ0)在凸集A上是C-凹的，那么Π(ε，λ0)是凸集.

證明：任取x1，x2∈Π(ε，λ0)?A和t∈[0，1]，那么tx1+(1-t)x2∈A，且對于所有y∈A，有

利用F的C-凹性，對于所有y∈A，有

F(tx1+(1-t)x2，y，λ0)+εe?tF(x1，y，λ0)+(1-t)F(x2，y，λ0)+εe+C?

t[F(x1，y，λ0)+εe]+(1-t)[F(x2，y，λ0)+εe]+C?C，

即tx1+(1-t)x2∈Π(ε，λ0)，從而Π(ε，λ0)是凸集.

2 主要定理和結果

由于已有文獻對精確解和近似解的存在性進行了深入研究，因此總是假定近似解集在參考點(ε0，λ0)附近是非空的.

定理1對于SVEP，假設在參考點(ε0，λ0)∈R+×Λ的鄰域內近似解存在，且

ⅰ)F(x，y，·)關于e∈intC在λ0處對于(x，y)∈A×A一致連續；

ⅱ) 對于所有y∈A，F(·，y，λ0)在凸集A上是C-凹的.

那么，Π在(ε0，λ0)處是Hausdorff連續的.

證明：令δ∈(0，ε0)，取集合N=(ε0-δ，ε0+δ)作為給定的ε0的鄰域.任取ε1，ε2∈N，其中ε1<ε2，實數η滿足0<η<ε2-ε1，由定理1的假設條件ⅰ)可知，存在λ0的鄰域Nη(λ0)，使得對于任意的λ1，λ2∈Nη(λ0)和x，y∈A有

F(x，y，λ2)?F(x，y，λ1)+η[-e，e].

(2)

對于任意的λ1，λ2∈Nη(λ0)，下證

Π(ε1，λ1)?Π(ε2，λ2).

(3)

設x∈Π(ε1，λ1)，則對于所有y∈A，有

F(x，y，λ1)+ε1e?C.

任取z2∈F(x，y，λ2)，由式(2)存在z1∈F(x，y，λ1)及c1∈C，使得z2=z1+η(-e+c1).從而有

z2+ε2e=z1+ε1e+(ε2-ε1)e-ηe+ηc1=z1+ε1e+(ε2-ε1-η)e+ηc1?C,

則F(x，y，λ2)+ε2e?C，?y∈A,即x∈Π(ε2，λ2).

由式(3)可知，對于任意的λ∈Nη(λ0)和ε∈N，有

Π(ε0-δ，λ0)?Π(ε，λ)?Π(ε0+δ，λ0).

(4)

對于滿足1

下證

(5)

任取x1∈Π(γ，λ0)，x2∈Π(ε2，λ0).由A的凸性可知k-1x1+(1-k-1)x2∈A，且對于所有y∈A，有

F(x1，y，λ0)+γe?C，F(x2，y，λ0)+ε2e?C.

因此，有

利用F的C-凹性，對于任意的y∈A，有

即

k-1x1+(1-k-1)x2∈Π(ε1，λ0).

由此可得到式(5)，并由式(5)可得到

則有

由于A是緊集，故它是有界的.因此，對于X中原點的任意閉凸鄰域V，存在ρ>0，使得A-A?ρV.因此有

(6)

Π(ε0，λ0)?Π(ε0-δ0，λ0)+V?Π(ε，λ)+V.

故Π在(ε0，λ0)處是Hausdorff下半連續.

在式(6)中，取ε1=ε0，ε2=ε0+δ0，k=ρ+1，可得到

Π(ε0+δ0，λ0)?Π(ε0，λ0)+V.

結合式(4)，可得出Π(ε，λ)?Π(ε0，λ0)+V，即Π在(ε0，λ0)處是Hausdorff上半連續.

注1當F為單值映射時，就得到了文獻[16]的定理1，定理1推廣了文獻[16]的定理1.

注2定理1的假設條件ⅱ)是必不可少的，如下例所示.

但由于

顯然有

因此，F的C-凹性條件不滿足. 近似解映射Π在(10-3，0)處不是Hausdorff連續的. 因為0∈

注3當F退化為單值映射時，上例改進了文獻[16]中的例1.

注4約束集的緊性條件不能刪除，如下例所示.

例2令X=R，Λ=[0，1]，A=(2，3]，Y=R，C=R+，e=1∈intC，ε0=10-3，λ0=0，且F(x，y，λ)=[λ(x-y)，λ(x-y)+1].易知滿足定理1的假設.通過計算可以得到

Π在(10-3，0)處非下半連續，由引理2可知，近似解映射Π在(10-3，0)處不是Hausdorff連續的.

與定理1的證明類似，可以得到集值向量均衡問題的對偶問題近似解映射Hausdorff連續性的充分性條件.

定理2對于DSVEP，假設在參考點(ε0，λ0)∈R+×Λ的鄰域內近似解存在，且ⅰ)F(y，x，·)關于e∈intC在λ0處對于(y，x)∈A×A一致連續；ⅱ) 對于所有y∈A，F(y，·，λ0)在凸集A上是C-凸的.那么，Πd在(ε0，λ0)是Hausdorff連續的.