你會數數嗎?

何文熙

分類列舉法

假如有人問你會不會數數，你一定會說：“這還用問嗎？誰不會數數哇！”其實，數數也不是一件簡單的事。比如：

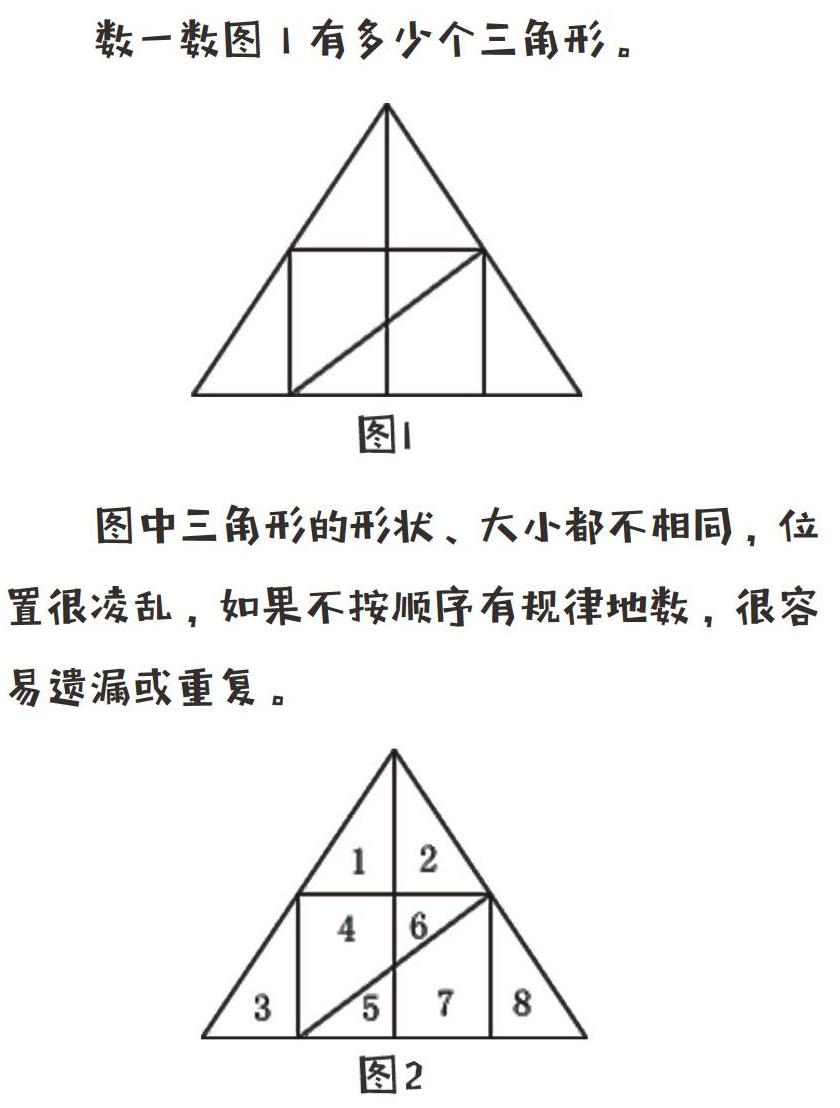
數一數圖1有多少個三角形。

圖中三角形的形狀、大小都不相同，位置很凌亂，如果不按順序有規律地數，很容易遺漏或重復。

此時，你可以按圖形的組成規律，把三角形分成單個的、由兩部分組成的、由三部分組成的……幾類，然后再按照組成部分的多少一類一類地數。為了便于觀察，還可以給各部分編上號。（如圖2）

這樣，就可以把每個三角形都簡明地表示出來。于是可以得到的三角形有：1、2、3、5、6、8共6個;由兩部分組成的三角形有：1-2、2-6、4-6、5-7，共4個;由三部分組成的三角形有：5-7-8，1個;由四部分組成的三角形有：1-3-4-5，2-6-7-8，2個;由八部分組成的三角形有1個。

所以一共有三角形：

6+4+1+2+1=14（個）。

這種方法就叫作“分類列舉法”。

“分類列舉法”注意事項：

①合理分類，不能遺漏。

②列舉要有順序性，要清楚明白。

列表法

還有一類問題，需要計數的不是具體的事、物或圖形，而是某種情況可能出現的次數。如：把10個橙子放在4個盤子里，每盤至少放1個，共有多少種不同的放法？

看到這個問題，相信你的第一想法一定是：只要4個自然數的和等于10，這組數就代表一種放法。可這樣的數不止一組，怎樣才能找全呢？

此時，你必須找到一種思考的順序和規律，才能使數數的過程有頭有尾，不重不漏。比如可以按照先少放后多放的原則，從第一個盤子放1個橙子開始，接下去使后面盤子里的橙子數盡量少，但又不少于前面盤子里的橙子數。然后依次增加前面盤子里橙子數。直到第一個盤子里的橙子數無法再增加為止……

把這個思考過程列成一個表，每一格代表一個盤子，每列4個數代表一種放法，很快就能求出全部答案。

從表中看出共有9種不同的放法。

這種方法叫作“列表法”。

圖解法

有時遇到的問題可能是由幾個相互連接的階段組成的，而每個階段又有幾種不同的選擇，情況就更復雜了。

一小學高年級有4個班，中年級有3個班，低年級有2個班。如果每天上美術課的只能是高、中、低年級的各一個班，那么每天上美術課的班級組成情況可以做到多少天不重復？

看完題目，是不是不知該從哪里著手？此時可以這樣做：

①用A、B、C、D代表高年級的4個班，用a、b、c代表中年級的3個班，用1、2代表低年級的2個班。

②確定從高年級中任意選出一個班以后，相應的中年級有3種不同的選擇，而對于中年級的任意一個班，低年級又有2種不同的選擇。

③畫示意圖，把思考過程清楚地表示出來。

于是得到4×3×2=24種不同的班級組成情況。

這種方法叫作“圖解法”。

現在，你會數數了嗎？