一個(gè)活躍在高考中的恒等式

張玉虎

(云南省施甸縣第一中學(xué) 678200)

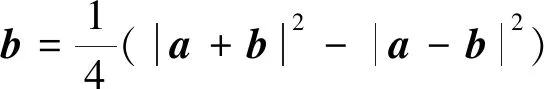
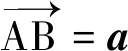
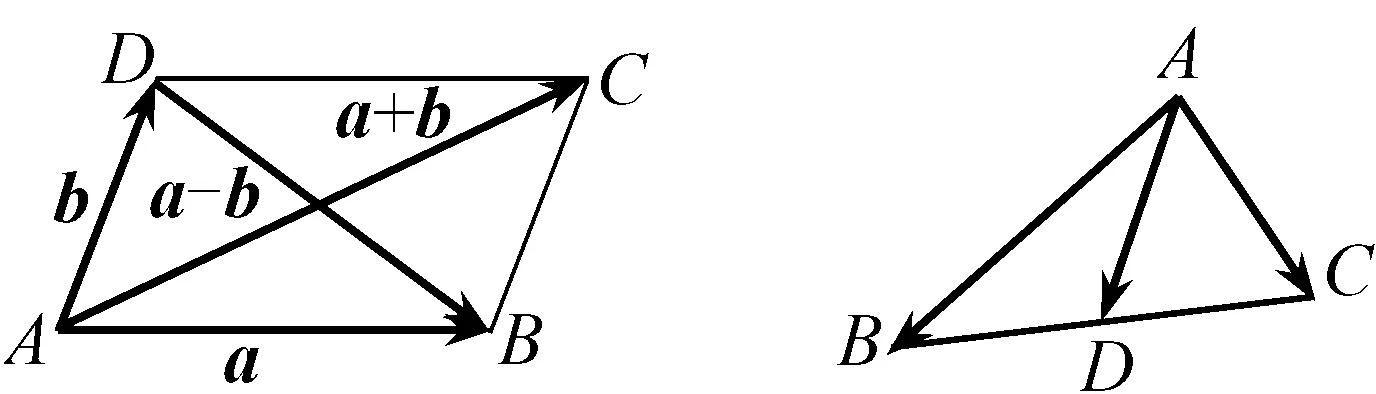
圖1 圖2

極化恒等式解決的是共起點(diǎn)兩向量的數(shù)量積問題，解決的關(guān)鍵是在第三邊上取中點(diǎn)，將多變量問題轉(zhuǎn)化為單變量問題，將向量的數(shù)量積轉(zhuǎn)化為向量的長度問題.在高考數(shù)學(xué)中，極化恒等式能將一些涉及向量的數(shù)量積問題化繁為簡、化難為易，從而使共起點(diǎn)向量的數(shù)量積問題得以快捷、高效地解決.

1 用極化恒等式求解數(shù)量積的值

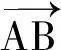
解析 如圖3，由極化恒等式可得

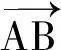
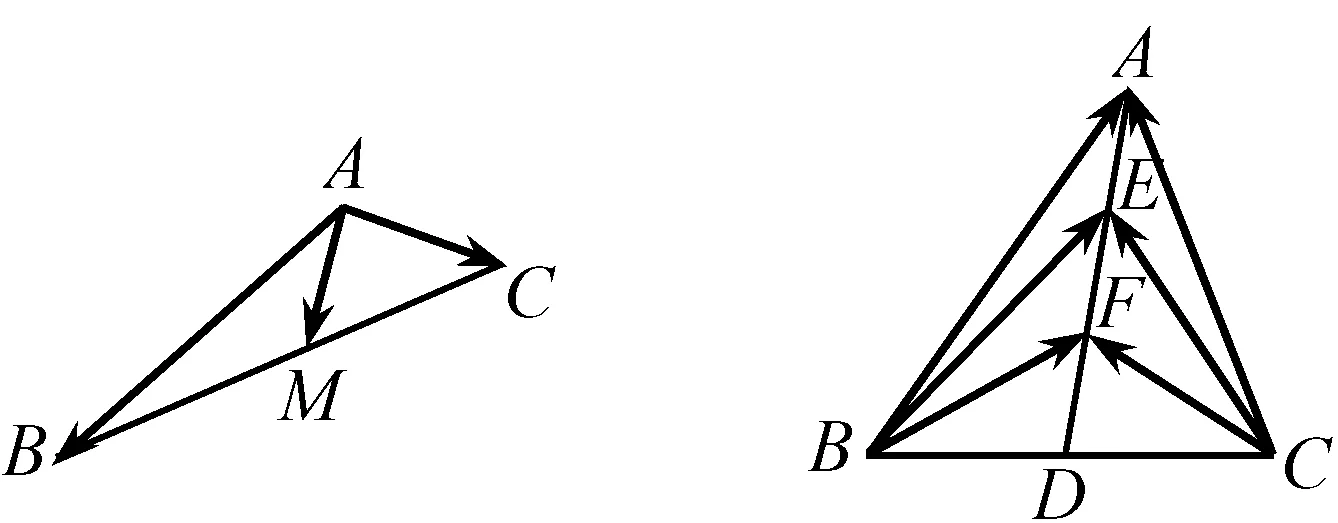
圖3 圖4

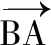
④《直齋書錄解題》可考的最晚撰寫年代是理宗淳祐五六年(1245-1246)，但因一直未付梓最后編定成書時(shí)間難定。詳參武秀成《陳振孫評(píng)傳》第二章《直齋書錄解題》的成書與流傳，南京大學(xué)出版社2006年版。

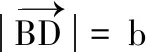
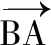
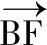
2 用極化恒等式求解與數(shù)量積有關(guān)的最值與范圍

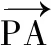
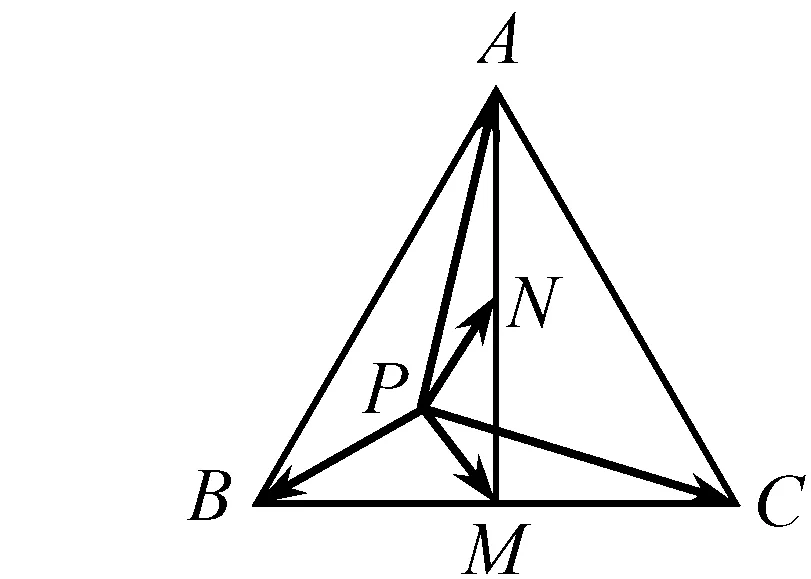
圖5

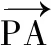
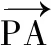
A.[2,6) B.[2,6]

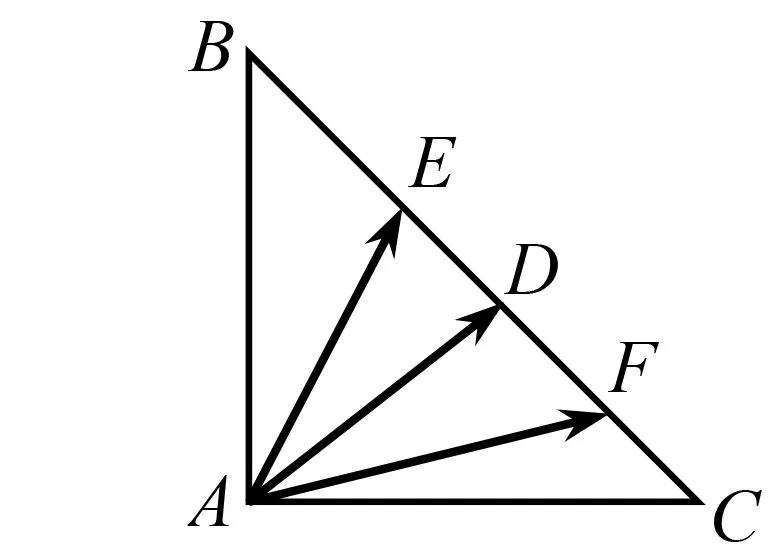
圖6

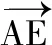
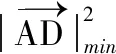
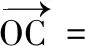
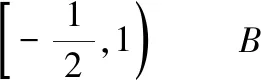
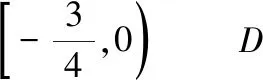
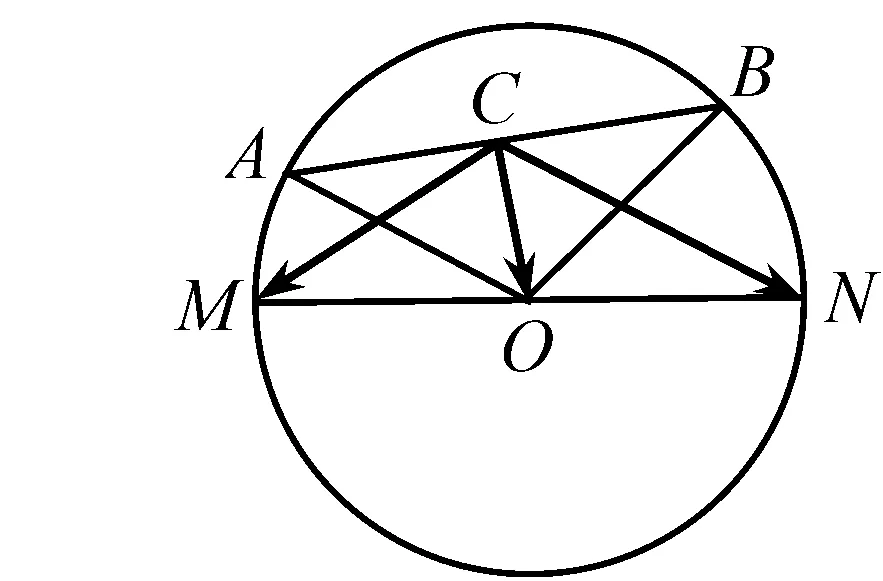
圖7

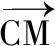
3 用極化恒等式求解圓錐曲線問題

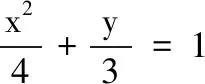
A.2 B.3 C.6 D.8

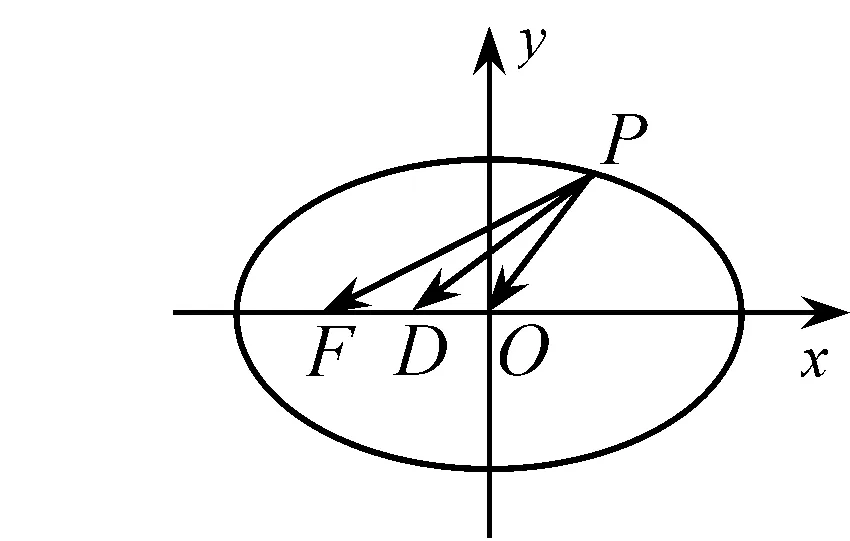
圖8

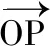
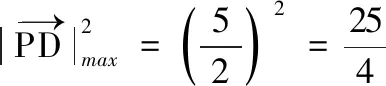
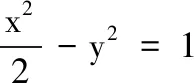
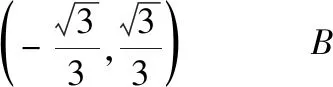
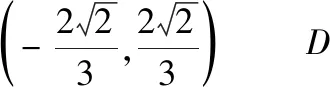
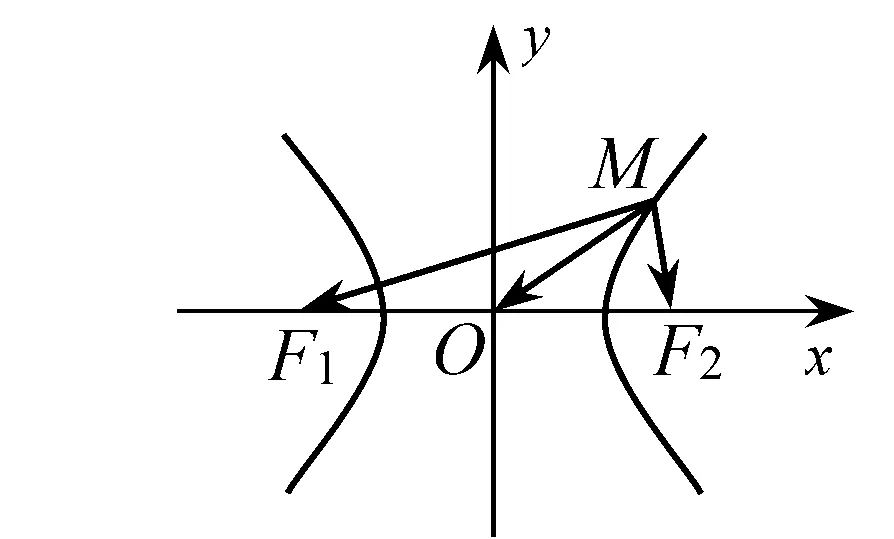
圖9

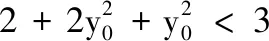
向量是高中數(shù)學(xué)的重要組成部分，是高中階段學(xué)生必須掌握的重要數(shù)學(xué)工具之一.其工具性主要體現(xiàn)在它是連接代數(shù)與幾何的橋梁，在求解數(shù)學(xué)問題中可以通過引入向量，借助向量的坐標(biāo)運(yùn)算與幾何運(yùn)算來解決問題.近幾年的高考數(shù)學(xué)試題越來越重視對(duì)向量運(yùn)用能力的考查，這已經(jīng)成為高考命題的一個(gè)熱點(diǎn)，而且在逐步向綜合性與靈活性方向提升.極化恒等式來源于教材而高于教材，構(gòu)建起了向量與幾何長度之間的互化通道，實(shí)現(xiàn)了向量與幾何、代數(shù)的之間的巧妙結(jié)合，優(yōu)化了解題方法，值得廣大考生去重視和思考.