一種空中目標航跡聚類方法研究*

梁復臺，李宏權，孟慶文，蔡莉

(1.空軍預警學院 預警情報系，湖北 武漢 430019；2.中國人民解放軍31121部隊，江西 南昌 330000)

0 引言

為挖掘歷史航跡價值、揭示空中目標活動規律，可對航跡進行聚類，得出聚類簇中心航跡，然后將中心航跡作為參考與實時空情比對，以幫助雷達操作員準確判定空中目標屬性，輔助指揮員及時對空情作出決策。

傳統的航跡聚類方法主要有基于航跡點的聚類、基于部分特征相似子航跡的聚類及面向航跡整體的聚類[1]。這些航跡聚類算法的關鍵點有2處：一是相似度度量模型的構建；二是高效聚類算法的設計[2]。其中，文獻[3]提出的航跡點逐點比對的航跡聚類方法，形成了一個航跡聚類框架。文獻[4]對文獻[3]的算法進行了改進，根據前后附近點最短距離來對航跡相似性度量，然后將聚類結果應用于終端區的進場程序管制。文獻[5]提出基于最長公共子序列相似性度量的聚類算法，根據航跡轉折點進行聚類，得到的聚類結果用于異常航跡預測。文獻[6]采用最小描繪長度(minimun description length,MDL)理論劃分得出航跡關鍵點，對關鍵點聚類采用改進的模糊k-means算法。文獻[7]提出了基于軌跡聚類的軌跡整體運動趨勢提取方法，聚類部分采取了分割再聚類的思路實現。

但這些傳統方法均存在著較多不足，基于航跡點的聚類運算量大，耗時長，占用大量資源，且對交叉航線航跡點較難處理；基于部分相似子航跡聚類算法復雜；面向航跡整體的聚類不能太多地兼顧航跡細節特征。針這些不足，本文提出一種空中目標航跡聚類算法，首先對空中目標歷史航跡進行曲線擬合，將其由點跡映射為曲線，然后對于曲線的特征點及參量運用k-means算法進行聚類，明顯克服了上述算法缺陷。

1 航跡特征提取

對于數據挖掘而言，提取有效的特征是前提，如果提取的特征對事物沒有好的區分度，方法再好也無濟于事。能將事物很好地區分開的屬性特征就是有效的特征，其有弱、中、強之分。能否找到強特征，很大程度上決定著數據挖掘的效率高低甚至數據挖掘的成功與否。

數據挖掘輸入的是樣本屬性。傳統關于航跡的數據挖掘方法，樣本的屬性多選擇為移動對象航跡的點跡[3-4]，或者基于復雜運算得到的特征點[5-6]，聚類模型往往都是建立于其上，算法運算量大，影響挖掘速度，算法時效性不高。本文通過航跡擬合得到航跡特征點及對應曲線參數，以此來表征目標活動規律的樣本屬性，帶來了一系列的優勢。

航跡是由大量點跡組成的，由于目標的運動軌跡是連續變化的，在一段連續的航跡上，點跡變化平緩，航跡曲線光滑，因此可利用曲線對航跡進行擬合。通過擬合曲線參數來代替大量點跡來進行聚類，得到航跡的參數化特征，減少了樣本屬性數量，使得算法可以適用于大的樣本集。同時還使得運算可以分階段進行，在傳輸及存儲階段進行擬合運算，在聚類階段只對擬合參數聚類，優化了存儲和運算資源，減小了數據傳輸壓力，提高了運算效率。

1.1 改進的航跡擬合算法

1.1.1 航跡擬合的基本方法

曲線擬合是指選擇適當的曲線類型來擬合觀測數據，并用擬合的曲線方程分析變量間的關系。常見的擬合函數有：指數函數、對數函數、冪函數，及多項式。對于空中目標航跡的擬合，考慮到多項式簡單易用，擬合計算速度快，擬合效果好，而成為空中目標航跡擬合的首選[8]。對大多數空中目標來說，為了得到較好的燃油經濟性并追求最大航程，都會盡快爬升到一定高度采取水平勻速巡航(巡航飛行)，盡量避免改變速度和高度，故航跡信息中高度值的變化較小，在一個很長的時間間隔內保留一個高度值即能反應高度的變化[9]。因此，可在經緯度構成的二維平面上采取用三次多項式y=ax3+bx2+cx+d曲線進行擬合[10]，擬合方法采用最小二乘法。目標函數為使航跡擬合值與點航跡實際值離差平方和(或稱殘差平方和)最小：

(1)

1.1.2 最優擬合區間的選擇

由于航跡軌跡復雜，用一條曲線難以描述其全部特征，故自適應的擬合區間選擇成為問題的關鍵[11]，且擬合區間應該精心選擇以達最優效果，過長或過短都會弱化重要特征點的區分作用，導致聚類誤差加大，況且，過小還影響壓縮效果，占用存儲空間。擬合前，首先將原始航跡極坐標轉換為直角坐標。然后采用回溯法對巡航階段航跡選擇最優擬合區間，回溯法的實現采用迭代逼近的方式：對于一段長度為L的航跡，假如誤差小于所設閾值，再向外延伸1/2距離，如果前后誤差相等，則終止循環并退出；如果誤差大于所設閾值，則從此判斷處往回縮減1/2距離，如此循環迭代，直至前后2次誤差相等，擬合誤差為

(2)

1.1.3 最優擬合區間段航跡擬合

采用上述擬合方法得出整條航跡的全部自適應擬合區間段，航跡段經度值記為序列Xm=(xm1,xm2,xm3,…,xmnm)，航跡段緯度值記為序列Ym=(ym1,ym2,ym3,…,ymnm)，其中，m為段落數，nm為第m段航跡點跡數目。然后對所有擬合區間段航跡附加如下限制條件重新擬合。

為保持航跡的連續性，對于第1段航跡需要添加這樣的限制條件，即該段首尾點值與擬合值一致：

(3)

對后面的最優擬合段(m≥2)擬合的過程中不但要考慮各段落之間的連續性，還需保證光滑性，即上一段的航跡末點為下一段的首點。

(4)

通過矩陣運算，將目標函數及其限制條件轉化為二次規劃問題[12]，通過在Python環境中調用函數計算，得到各段擬合曲線參數。擬合后的航跡信息用航跡擬合特征點與其所對應擬合區間的擬合曲線參數來表示：[(經度，緯度)，(a,b,c,d)]。

1.2 算法仿真實驗

按照上節所述思路，用python語言編程實現算法，然后對一條航跡采用該擬合算法進行仿真，得出航跡位置信息擬合前后效果對比示意圖。此段航跡共包含373點跡(圖1藍色點跡所示)，航跡地理位置信息變化明顯，比較真實地反映了各類空中目標航跡特征，具有一定的代表性。

圖1 固定劃分航跡擬合圖

文獻[8]的軌跡擬合算法對航跡段落進行了固定劃分，雖然一定程度上解決了擬合效果不好的問題，但在段落劃分較少時還是存在著與真實航跡偏差太大的問題，如果劃分過密，又達不到壓縮數據量的目的。圖1中分段數達到35，擬合曲線才較好地吻合原航跡。

圖2 自適應的航跡擬合圖

對于自適應的航跡擬合方法，在不附加限制條件的情況下，擬合誤差σ=0.000 01時，紅色圓圈表示擬合特征點，紅色曲線為與擬合特征點對應的擬合曲線。從圖2可以看出，航跡在自適應擬合段的連接處出現斷續，且每段之間連接不光滑，模擬真實航跡存在著一定的失真。

采用本文中所示方法，在擬合誤差σ=0.000 01時，自適應航跡段數目為8，原始航跡曲線與擬合后的曲線吻合很好，連續性及光滑性都得到了很好的體現，見圖3。很好地保留了航跡信息特征，實現了航跡信息存儲與挖掘分析以及可視化各方性能的兼顧。

圖3 改進自適應擬合航跡圖

2 基于k-means的航跡聚類

聚類是一種無監督學習，將對象劃分為不同的簇，同一個簇中的對象“相似”，不同簇之間對象“互異”[13]。聚類方法有基于原型的方法、基于層次的方法、基于密度的方法、基于網格的方法和基于模型的方法。基于原型的聚類方法中，對象的相似性通常通過距離函數來度量，這個特點適用于對于航跡信息的聚類。基于原型的聚類方法常用的有k均值，k-means++是它的改進型，解決了k-means方法因初始中心選擇不當導致簇效果不佳或收斂慢的問題[14]。本文采用k-means++算法實現聚類，簡記為k-means算法。

2.1 航跡特征點聚類

k-means算法的基本思想是：首先從特征集中隨機選擇k個特征點作為初始簇中心；然后將n個數據對象劃分為k個簇以便使其距離滿足：同一簇中的對象相似度較高；不同簇間的對象相似度較小。k-means++在初始點的選擇上作了優化。給定樣本集D={x1,x2,…,xm}，聚類所得簇C={c1,c2,…,ck}最小化平方誤差：

(5)

通常對“相似度度量”都是基于某種形式的距離來定義，距離大小與相似度大小成反比。最常用的距離是閔可夫斯基距離，對于給定樣本xi=(xi1，xi2，…，xin)與xj=(xj1，xj2，…，xjn),有

(6)

當p=2時閔可夫斯基距離就是歐式距離,當p=1時為曼哈頓距離[15]。在本文中，采用了歐式距離作為相似度的度量。

對整段航跡通過選取自適應擬合段落，得到各段航跡特征點及擬合曲線系數，建立起關于整段航跡的新的特征集。對某空域中所有航跡擬合時選取統一的誤差閾值，得到的新的航跡特征集則能夠代表原航跡，解決了傳統以所有航跡點作為航跡特征來聚類，所帶來的運算量大、準確率不高的問題。對1.1節所述航跡采用自適應航跡擬合算法，將原航跡373點跡壓縮為8個特征點，數據量減少了98%,除去擬合環節的開銷，在聚類環節，運算量相應減少了98%，這在實時航跡匹配中可以提高運算速度。

k-means算法的缺點是必須事先指定先驗的簇數量[16]。對于航跡數據聚類中心數目的確定，可以事先根據擬合特征點的分布，經可視化處理最終確定，也可以通過二分k-means或通過肘部法和輪廓系數圖對聚類效果進行評定，幫助選出最優k值。本文采取肘部法評估、可視化輔助的方法選定最優k值。

2.2 航跡曲線系數聚類

對最優航跡擬合段特征點進行聚類，還存在準確率不高的問題，在此基礎上，結合航跡最優擬合段曲線系數聚類，可以形成印證互補，提高正確率。

多項式系數決定著多項式曲線的形狀，從系數上能夠區分擬合曲線所表示的航跡。可對于三次多項式擬合所產生的4個系數，較難在其上確定“序”的關系，屬于無序屬性，不能直接用閔可夫斯基距離來度量[17]。

對本文中航跡擬合所采取的三次多項式求導可得y′=3ax2+2bx+c，取Δ=4b2-12ac，Δ=0是其是否單調的臨界點，再通過a值的大小，完全可以確定目標航跡的運動特征。通過觀察三次函數圖像(如圖4所示)，不難發現a與Δ決定著曲線的形狀及性質。a的大小決定函數曲線遞增與遞減性，Δ的大小決定著函數曲線的單調性。故本文中將系數(a,b,c,d)轉化為(a,Δ)2個屬性來表述擬合航跡段。

圖4 三次函數圖像及性質

在實際的聚類操作中，這2類屬性具有不同的量綱，這樣會影響到航跡聚類的結果，為了消除屬性之間的量綱影響，需要進行屬性數據歸一化處理，以使航跡之間具有可比性。本文采用min-max normalization的歸一化方法，特征量化的公式為

(7)

考慮到現實中曲線的遞增與遞減較明顯地表示了航跡的走向，而單調性對航跡的區分沒有太大的影響，這里采用加權的閔可夫斯基距離來進行相似度度量：

(8)

根據多次的嘗試，式(8)中的權值確定為w1=0.7,w2=0.3較合適。

2.3 實驗分析

2.3.1 航跡特征點聚類效果

(1) 誤差閾值的影響

模擬某空域一段時間航跡軌跡數據，有3類23條航跡，共4 051點跡，在對其運用自適應擬合方法后，得到航跡特征點集，對其采用k-means方法聚類后效果如下：

誤差閾值取0.000 01時，得到共141個航跡擬合特征點，雖然能夠很精細地體現航跡特點，但對于航跡聚類來說，聚類的效果不理想，只有一類5條航跡完整地分辨了出來，見圖5。誤差閾值取0.000 1時，得到共58個航跡擬合特征點，擬合精細度較上次有所降低，聚類的效果有提高，但還是不夠完美,將一類折返航跡分成了2類航跡，如圖6所示。

誤差閾值取0.001時，得到共33個航跡擬合特征點，由圖7可以看出，聚類結果將3類航跡完全區分了出來。由此看來，誤差閾值的取值與擬合精細度成反比，與聚類效果成正比，在不是航跡重現的場合，可以放寬閾值的設置來達到更好的聚類效果。

(2) 最優簇數目k值的確定

按照肘部法的思路，先用航跡總數作為k值代入聚類，逐次遞減，監控在該過程中所有樣本點到其所屬類簇距離的平方和，在該值明顯出現肘部時所對應的k值即為最優簇數。

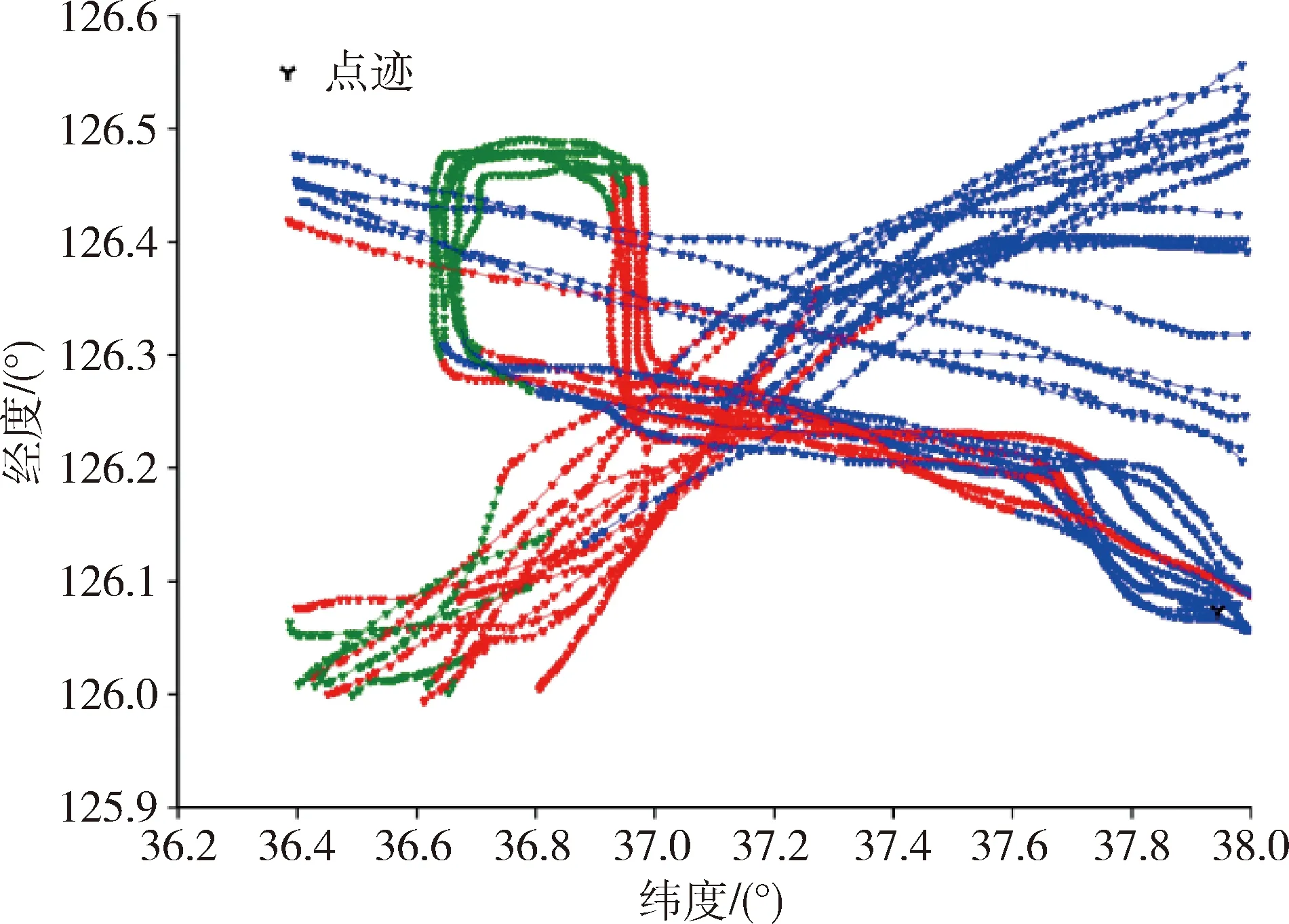
圖5 誤差閾值取0.000 01時

圖6 誤差閾值取0.000 1時

圖7 誤差閾值取0.001時

由圖8可看出，對2.2節所述空域航跡聚類，k值最后確定為3，這個和現實中的航跡類別數目相吻合(參見圖7)。

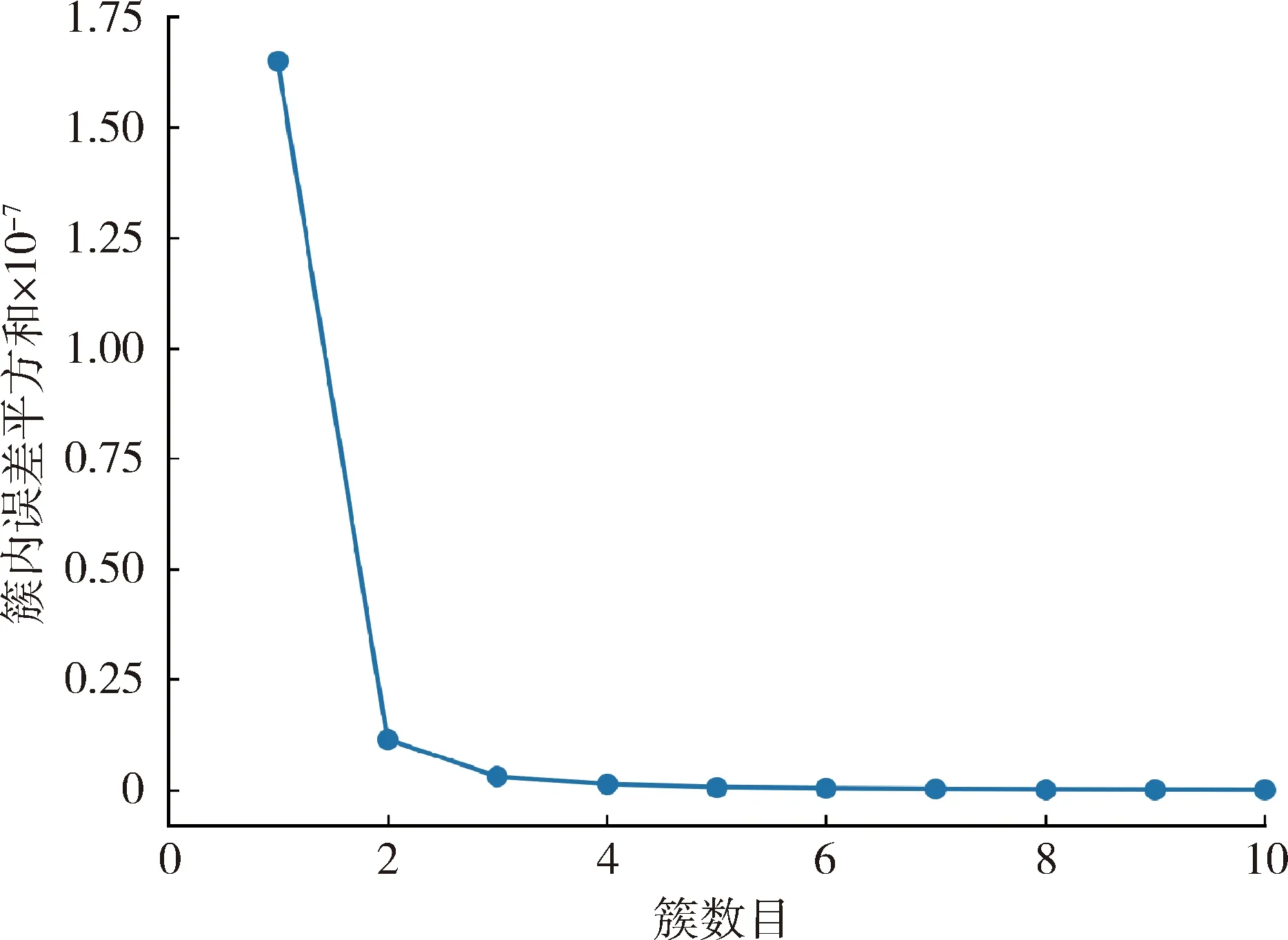
圖8 肘部法確定最優簇數目k值

2.3.2 航跡曲線參數聚類效果

對于交叉的航跡，對于航跡點采用聚類方法包括k-means、DBSACND(基于密度的聚類算法)都無能為力。從2.3.1節實驗可以看出，在擬合誤差閾值取較小時，擬合特征點跡數量較多，存在不同航跡特征點同在一個簇中，但特征點對應的航跡曲線不屬于同一類型的情況，即存在航跡交叉現象，此時難以有效區分航跡，聚類效果不好。在對自適應擬合段特征點聚類的同時，結合擬合段曲線參數聚類，可以提高聚類航跡聚類效果。經實驗，在結合特征點曲線系數聚類后，對航跡的聚類性能提升明顯，誤差閾值取0.000 1時，仍然可以實現航跡正確聚類。

3 結束語

針對傳統航跡聚類算法計算量大、實時性差等問題，本文首先提出了自適應的航跡擬合算法，從原始航跡中提取少量特征點及對應的擬合曲線，然后采用k-means方法對特征點進行聚類，從而實現了航跡的聚類區分。通過實驗仿真可以看到，選取合適的誤差閾值可以實現大量航跡的有效聚類，可以將不同運動特征的航跡區分開來。在運用到真實航跡聚類時，為使得算法效果更好，可結合航跡信息所表征的空中目標運動屬性，如飛行高度、速度、加速度、爬升率等，以更精準地實現空中目標航跡聚類。