基于相位差變化率的無源定位及誤差分析*

姜智強，山世浩，張恒，黃烽

(中國洛陽電子裝備試驗中心,河南 洛陽 471003)

0 引言

在現代電子對抗斗爭中，無源偵察定位技術因其具有不需向外輻射電磁信號，且具有較好的隱蔽性、較強的生存能力等特點[1]而受到各國重視。在無源偵察定位技術中，基于相位差變化率的無源定位技術因其具有可實現單站快速定位、作用距離遠、可在敵方作戰載體的火力范圍外實施定位、體積小、成本低等優點而得到了廣泛應用[2]。因此，分析研究基于相位差變化率的無源定位技術，將會對無源偵察定位技術的發展有很大幫助。

基于相位差變化率的無源定位技術是通過測量目標輻射源的方位角、信號載頻及相位差變化率等參數實現對目標偵察定位的技術。主要應用態勢包括固定觀測站對運動輻射源的定位、運動觀測站對固定輻射源的定位以及運動觀測站對運動輻射源的定位；不同的對抗態勢，其可觀測性條件[2]不同。

本文主要針對運動觀測站對固定輻射源的場景，進行了基于相位差變化率的二維無源定位原理分析[3]，研究了影響定位誤差的主要因素，并對測向誤差和相對測距誤差進行了仿真分析。

1 基于相位差變化率的無源定位原理

基于相位差變化率的無源定位技術原理[4]如圖1所示，當運動觀測站以速度v沿x軸作勻速直線運動對固定目標輻射源進行定位時，假設某一時刻觀測站位置為O(xoi,yoi)，此位置可由飛機自身導航設備獲取；固定目標輻射源位置為T(xt,yt)，相對觀測站的方位角為β，與觀測站之間的距離為R。根據其位置關系，則有

(1)

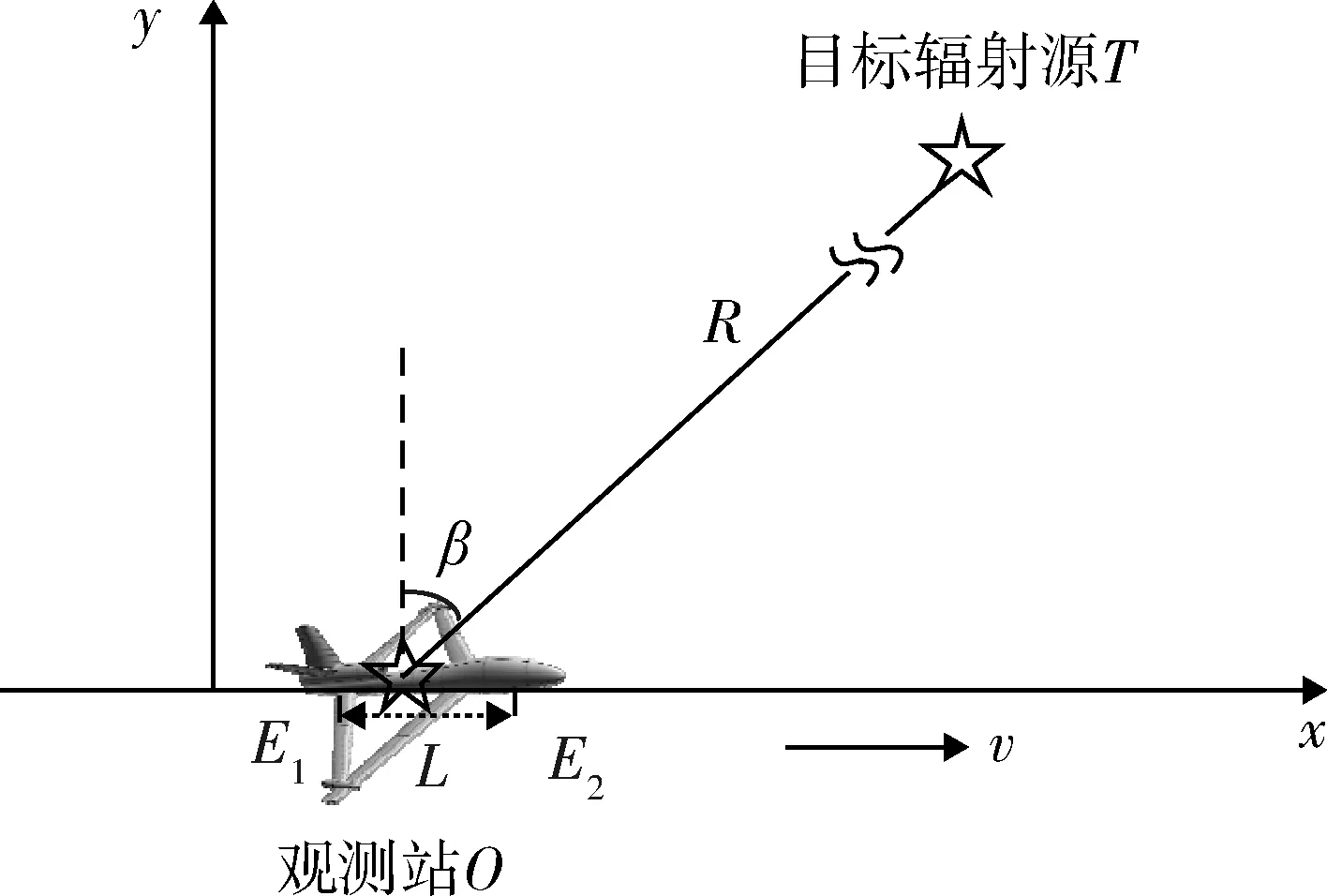
圖1 基于相位差變化率無源定位原理圖

由以上關系可知，基于相位差變化率無源定位的核心問題是利用干涉儀天線陣獲取目標方位角和相對距離。

1.1 干涉儀測向

干涉儀測向的原理[5-6]如圖2所示，相位匹配的雙陣元天線E1,E2固定在觀測站載機身上，基線長度為L。當對波長為λ的輻射源信號進行偵察時，由于信號到達兩陣元天線的時間有先后(天線陣連線的法線方向除外)，導致天線陣接收到的信號存在相位差。

圖2 干涉儀測向原理圖

兩天線接收到信號的相位差φ可表示為

(2)

目標輻射源相對觀測站的方位角可表示為

(3)

由于鑒相器無模糊檢測的范圍為[-π,π)，所以單基線干涉儀無模糊測角的范圍為[-θ,θ)。

(4)

由式(4)可以看出，無模糊測角范圍與λ/L成正比，要在空域上獲得較大的無模糊測角范圍，就要盡可能提高λ/L值。

1.2 干涉儀測距

干涉儀測距的原理[1，7-10]如圖1所示，當觀測站相對目標輻射源作切向運動時，觀測站與目標輻射源之間的距離R可表示為

(5)

如圖3所示，觀測站相對目標輻射源的切向速度[10]voβ可表示為

voβ=vxcosβ-vysinβ,

(6)

圖3 觀測站相對運動示意圖

式中:vx,vy分別為觀測站x,y向速度分量。

對式(2)求方位角β的導數可得

(7)

將式(6)，(7)代入式(5)可得

(8)

2 定位誤差分析

通過對基于相位差變化率無源定位的原理分析可知，對目標輻射源的定位誤差[11]主要由測向誤差和測距誤差2部分組成。

2.1 測向誤差分析

對式(2)求全微分可得

(9)

從式(9)可以看出，影響干涉儀測向誤差的主要因素是相位差誤差和測頻誤差，且與目標方位角、天線基線長度、信號載頻有關。測向誤差與λ/L成正比，要獲得較高的測向精度，必須設法減小λ/L值，但減小λ/L值的同時，無模糊測角的范圍也相應減小。因此，在實際應用中，通常采用長基線、多基線等措施，來進一步提高測向精度和消除在寬空域上的測量模糊。

2.2 測距誤差分析

當觀測站沿x軸作勻速直線運動時，其y向速度分量為0，即vy=0。式(8)可簡化為

(10)

對式(10)求全微分，可得：

(11)

在無源偵察系統中，往往以相對測距誤差的大小作為系統測距精度的評估指標。

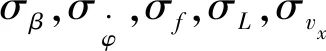
(12)

由式(12)可知，相對測距誤差[12]與信號載頻f、基線長度L、觀測站飛行速度vx成反比，信號載頻越高、基線越長、觀測站飛行越快，則相對測距誤差越小。實際應用中觀測站測頻誤差σf一般不大于3 MHz，其相對雷達信號載頻小得多；基線長度的測量誤差σL一般不大于0.01 m，遠小于天線陣基線長度；σvx為機載導航設備的測速誤差，一般不大于1 m/s，相對載機速度要小得多。

因此，影響相對測距誤差的主要因素為目標輻射源方位角及其測量誤差、信號相位差變化率及其測量誤差。

3 仿真分析

3.1 測向誤差仿真分析

由式(9)可知，當基線長度固定時，影響測向誤差的主要因素為相位差誤差。當信號載頻為1 GHz，基線長度為1 m時，目標輻射源方位角變化及相位差誤差對測向誤差的影響如圖4所示。

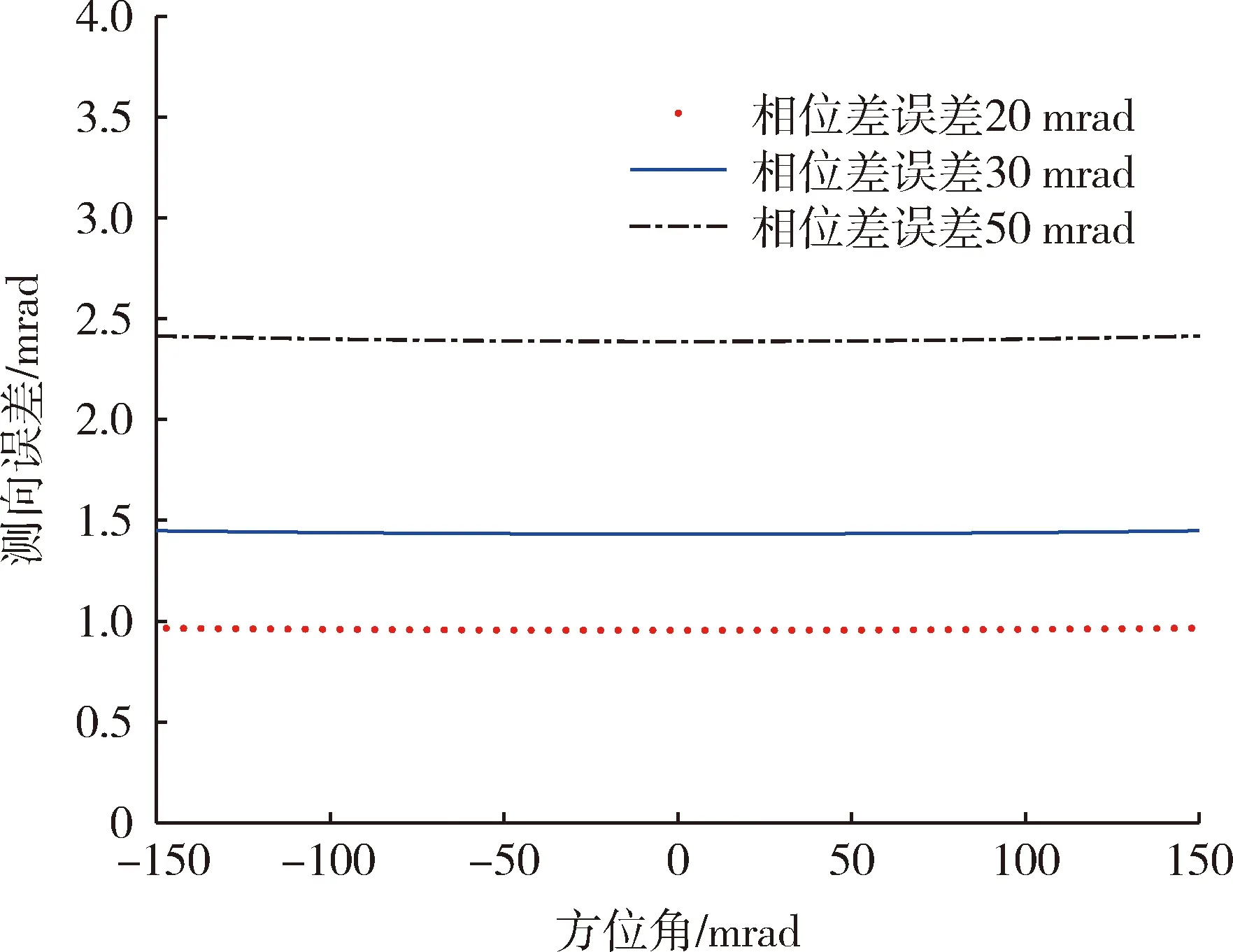
圖4 測向誤差與方位角、相位差誤差關系圖

由圖4可以看出，當相位差誤差相同時，在測向角無模糊范圍內，測向誤差變化不大；當方位角相同時，隨著相位差誤差的增大，測向誤差隨之增大。仿真數據顯示，當相位差誤差為50 mrad時，測向誤差小于2.5 mrad，一般遠小于觀測站的測向精度要求(測向精度要求一般為3°，約52 mrad)。

3.2 相對測距誤差仿真分析

當觀測站對固定目標輻射源進行單次測距時，取f，L，vx，σvx，σf，σL的值分別為6 GHz，5 m，300 m/s，1 m/s，3 MHz，0.01 m，則不同測向誤差、相位差變化率誤差對相對測距誤差(百分比)分布的影響如圖5所示。

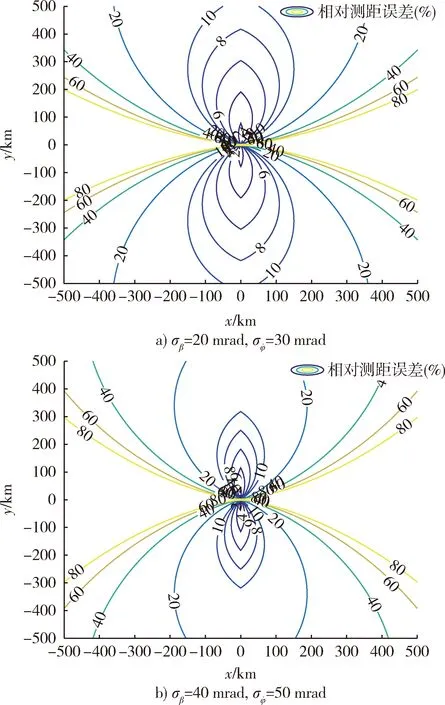
圖5 相對測距誤差(百分比)分布圖

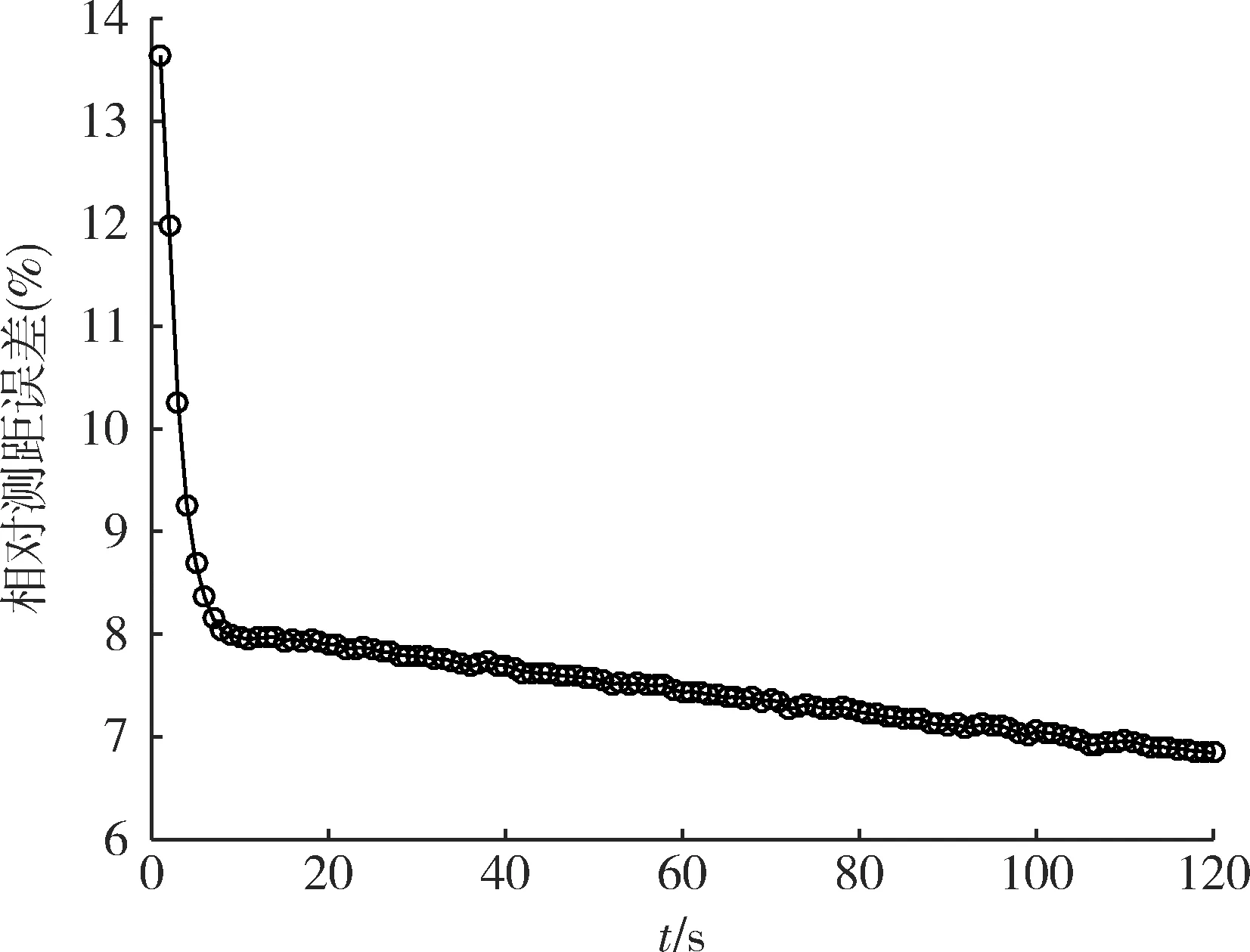
圖6 相對測距誤差收斂曲線圖

從圖6可以看出，對測距數據采取擴展卡爾曼濾波算法處理后，相對測距誤差快速下降，能夠在較短時間內提高測距精度，從而提高對目標輻射源的定位精度[15]。

4 結束語

本文在對基于相位差變化率的無源定位技術原理進行分析的基礎上，研究了影響定位誤差的因素，結果表明，測向誤差及相位差變化率誤差是影響定位誤差的主要因素；并利用觀測站的運動特性，對測距數據采用相關濾波算法處理，實現了相對測距誤差的快速收斂，從而較好實現了運動觀測站對固定目標的無源定位。