深糾錯因 改進教學
陳香君 湯強
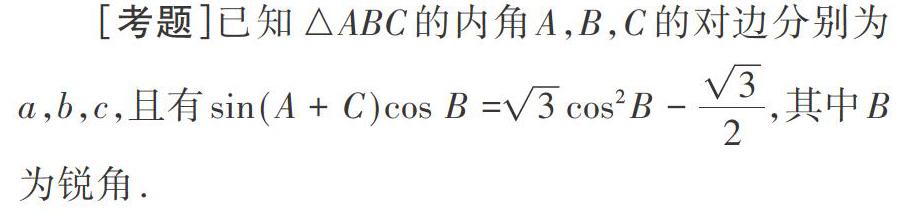


[摘要]學生在解答一道考題時錯誤多多,因此從理解題目的信息障礙、分析題目的推理障礙及解答題目的運算障礙對學生解答考題時的錯誤進行深度剖析,對學生考題的錯誤進行深度剖析,可以提高學生的解題能力,可以為教師改進教學提供目標和方向。
[關鍵詞]考題,錯誤,教學,剖析
[中圖分類號]G633.6[文獻標識碼]A [文章編號]1674-6058(2020)11-0001-02
在一次考試中,學生在解答一道曾經做過、教師也講過的考題時錯誤多多,這讓我們不得不反思針對此題的相關教學,因而,對學生的錯誤進行深度剖析就顯得尤為必要。
一、學生答題的整體情況
(1)求角B;
(2)若b=1.求△ABC面積的最大值,
第(1)問考查三角形中正余弦的轉化以及二倍角公式;第(2)問綜合考查余弦定理和基本不等式,
從得分情況看,文科的平均分為3.02分,理科的平均分為5.29.整體得分情況為得0分、6分和12分(滿分)的較多,得3分、8分和10分的較少,試題難易情況和得分高低情況并不相符,說明對學生失分原因進行深入分析是必要的,
二、學生的解題錯誤分析
1.基于信息障礙的錯誤
此題題干中,既有邊又有角,還有邊角之間的數量關系,學生難以獲得有用信息,
2.基于推理障礙的錯誤
3.基于運算障礙的錯誤
第一種,三角函數值記憶不準,
三、教學改進
1.教會學生捕捉有效信息。從現今的“大數據”到2017年版普通高中數學課程標準提出的“數據分析”核心素養,無不說明,學會對已有信息的分析,是學生一項必備的能力,通過審題,捕捉題干中的有效信息,進而利用這些信息答題也應是學生的一項重要能力,因此,在教學中教師要教會學生捕捉有效信息,
2.培養學生邏輯思維,數學是以嚴密邏輯著稱的學科,數學學科的培養目標是讓學生學會用數學眼光觀察世界,用數學思維思考世界,用數學語言表達世界,要實現這個目標,培養學生的邏輯思維是必不可少的。
3.幫助學生夯實基礎記憶,張奠宙教授曾說:“記憶通向理解,”雙基作為我國數學教學的優良傳統,也強調數學學習是需要一定的記憶的,以我們切身經歷看,對三角形全等的判定方法以及特殊三角函數值等的記憶確實能提高學生的計算能力,當然,記憶和理解是要相結合的,一味地記憶只會使學生知其然而不知其所以然。
4.幫助學生理解公式。公式“繁雜”是很多學生對數學的共識,出現這種看法的很大一部分原因是學生對公式的理解不到位,這既與學生不重視公式的推導過程,只記憶的結果有關,也與教師有時未向學生介紹公式的來龍去脈,將公式直接拋給學生有關,因此,學生應重視對公式的理解,只有理解透徹后才能運用自如。
5.培養學生運算能力。數學運算實際上屬于“數學基本技能”中的一部分,是最重要的,張奠宙教授的另一觀點是“速度贏得效率,應將基本的運算和基礎的思考換化為直覺,從而贏得更多的時間以便于進行高層次的數學思維活動”,可見,培養運算能力是走向高層次數學學習的必經之路。

