基于模糊控制的移動機器人局部路徑規劃

郭 娜，李彩虹，王 迪，張 寧，宋 莉

(山東理工大學 計算機科學與技術學院, 山東 淄博 255049)

移動機器人可以在某些環境尤其是惡劣環境下代替人類完成相應的工作，這使得移動機器人的研究在國內外受到廣泛關注，而路徑規劃作為移動機器人完成某項工作的基礎功能顯得尤為重要，如何快速、準確地規劃路徑成為移動機器人領域的一大研究熱點[1]。

移動機器人的路徑規劃包含全局路徑規劃和局部路徑規劃[2-3]。全局路徑規劃是在機器人位姿、環境和目標都已知的情形下，尋找一條從起始位置到達目標位置的無碰撞最優路徑。局部路徑規劃是在運行環境未知的情況下實時地規劃路徑，移動機器人由于傳感器探測距離有限以及周圍環境的不確定性,很難從整體最優上進行路徑規劃,因此機器人從局部最優進行路徑規劃[4-5]。

局部路徑規劃的方法主要有人工勢場法、模糊控制法、遺傳算法、神經網絡等[6-7]。人工勢場法由于其操作簡單、應用性強被廣泛使用，但易出現因受力平衡導致局部震蕩無法到達目標點的情況[8]。模糊控制具有較好的實時性[9]，模擬了駕駛員在駕駛過程中面對各種情況作出反應[10-11]，但在復雜環境下，如U型障礙，易出現死鎖的現象。針對這種現象李擎等[12]設計了U型槽模糊控制器，能夠解決U型障礙物的死鎖問題，但只是針對障礙環境已知的情況下，在未知環境下并不通用。魏立新等[13]通過機器人旋轉角度來判斷是否進入和逃脫U型陷阱區取得了很好的效果，但在其他障礙情況下是否依然可行還有待驗證。Aouf等[14]設計了去目標障礙和墻跟隨的行為仲裁方法，可有效避免與凹凸障礙物的碰撞。本文針對傳統模糊控制算法中存在的死鎖問題，首先設計模糊控制器，設置模糊規則，然后加入障礙逃脫策略和轉向策略，在各種障礙物環境下進行仿真研究。

1 模糊控制器的設計

設計模糊控制器首先要根據實際需要確定輸入量和輸出量，確立模糊語言變量，選擇合適的隸屬度函數[15]，根據人類經驗設計模糊控制規則[16]。本文采用模糊控制的方法，模仿人行走時行為的推理和決策過程，由測得的與障礙物的距離推理下一步的前進方向和步長。

1.1 確定輸入量和輸出量

移動機器人上安裝了三個距離傳感器，分別為正前方M、左方L和右方R，左右方向都與正前方相差30°，正前方是面向目標點的方向，如圖1所示。

模糊控制器是雙輸入、雙輸出的結構，其中輸入量為機器人正前方即目標點方向距障礙物的距離dM、左邊距障礙物的距離減去右邊距障礙物的距離dLR。輸出量為機器人下一步前進方向的轉角Angle以及步長Step，結構如圖2所示。

圖1 移動機器人探測方向Fig.1 Detection direction of mobile robot

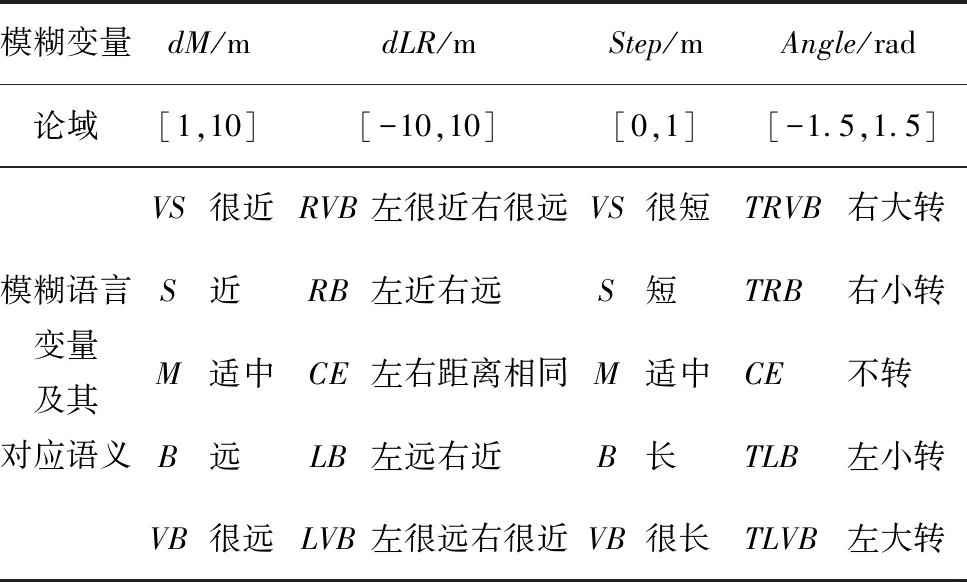
模糊控制器的輸入量要進行模糊化，也就是需要把確定的輸入量轉化為模糊向量。表1給出了模糊變量的論域、劃分情況和語義對照。

以輸入量dLR中的RB為例，RB是一個表示距障礙物左近右遠的模糊集合，μRB(x)表示元素x屬于集合RB的程度，取值范圍為[0,1]，稱μRB(x)為x屬于模糊集合RB的隸屬度。當模糊集合RB由連續函數構成，各元素的隸屬度就構成了隸屬度函

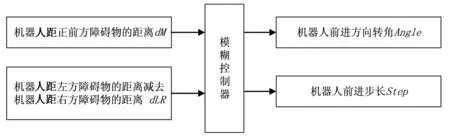
圖2 模糊控制器結構圖Fig.2 Structure of fuzzy controller

表1 模糊語言變量語義對照表
Tab.1 Semantic comparison of fuzzy linguistic variables

模糊變量dM/mdLR/mStep/mAngle/rad論域[1,10][-10,10][0,1][-1.5,1.5]模糊語言變量及其對應語義VS很近RVB左很近右很遠VS很短TRVB右大轉S近RB左近右遠S短TRB右小轉M適中CE左右距離相同M適中CE不轉B遠LB左遠右近B長TLB左小轉VB很遠LVB左很遠右很近VB很長TLVB左大轉

數μRB(x)，此時模糊集合RB表示為

(1)

隸屬度函數是用于表征模糊集合的數學工具，本文選用梯形隸屬度函數，使用主觀經驗法來確定。梯形曲線可由4個參數a、b、c和d確定，RB的隸屬度函數可表示為

(2)

通過確定各個模糊集合的隸屬度函數參數，確定隸屬度函數。輸入量dM的隸屬度函數如圖3所示，其余輸入輸出量隸屬度函數與dM的相同。

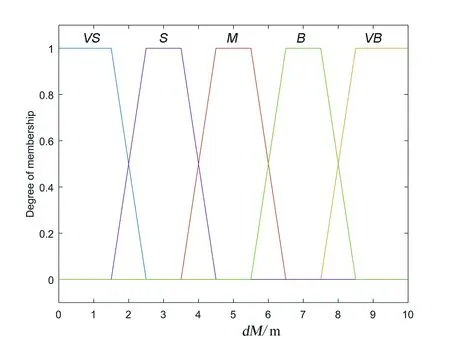
圖3 輸入量dM的隸屬度函數Fig.3 Membership function of input dM

1.2 設置模糊規則

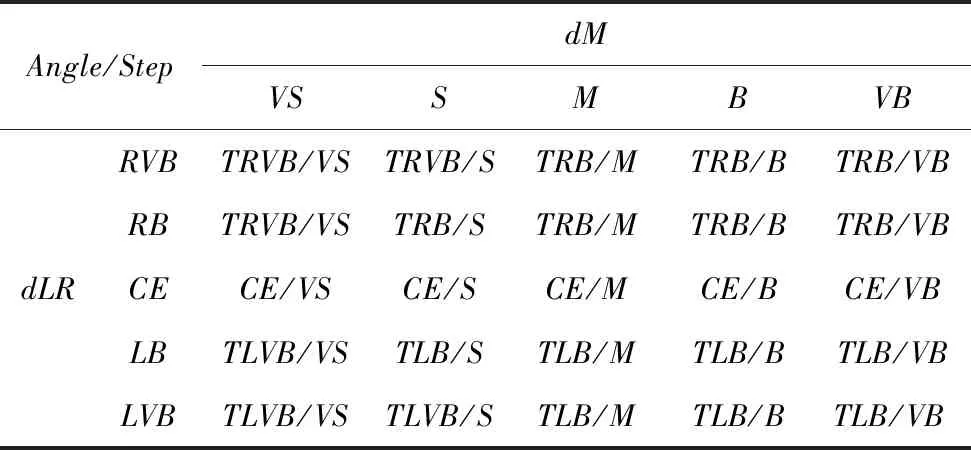
模糊控制器規則的設置是根據駕駛員駕駛汽車的經驗，并將左、右兩個傳感器探測到的障礙物距離做差，減少了輸入量，精簡了規則數量。根據此方法一共設計了25條規則，見表2。

表2 模糊控制規則
Tab.2 Rules of fuzzy control

Angle/StepdMVSSMBVBdLRRVBTRVB/VSTRVB/STRB/MTRB/BTRB/VBRBTRVB/VSTRB/STRB/MTRB/BTRB/VBCECE/VSCE/SCE/MCE/BCE/VBLBTLVB/VSTLB/STLB/MTLB/BTLB/VBLVBTLVB/VSTLVB/STLB/MTLB/BTLB/VB

根據不同方向距障礙物的距離不同，確定合適的模糊規則，當輸入量dM為VS，dLR為RVB時，輸出量Step為VS，Angle為TRVB，則模糊控制規則表示為：

If (dMisVS) and (dLRisRVB)

then (StepisVS) (AngleisTRVB)

根據表2模糊控制規則的設置，得到了輸入量和輸出量的關系，如圖4所示。

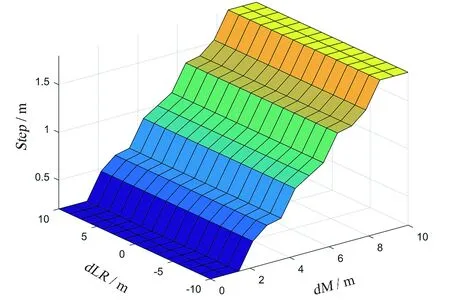
(a)Step與dM、dLR的關系

1.3 模糊推理與解模糊

常用的模糊推理有兩種方法：Zadeh法和Mamdani法。Mamdani推理法是在模糊控制中普遍使用的方法，其本質是一種合成推理方法，本文采用Mamdani法進行模糊推理。

以dM= 6.93 m、dLR= -6.99 m為例，在圖5所示的規則查看器中可以看出，在此狀態下觸發了模糊規則第21條和第24條，按照對規則取極小值和取極大值的方法，得到輸出值。在第21條規則中選取極小值dLR中RVB的隸屬度函數，在第24條規則中取極小值dLR中RB的隸屬度函數，兩條規則得到的隸屬度函數再各自取極大值即可得到兩個輸出量的隸屬度函數。

圖5 模糊控制規則查看器Fig.5 Fuzzy control rule viewer

經模糊推理得到的推論結果是模糊量，要對其進行解模糊，將模糊量轉化為精確量。解模糊的方法有：最大隸屬度法、重心法和加權平均法等。最大隸屬度法的優勢是簡單，選取模糊集合中隸屬度最大的元素作為輸出值，適用于控制要求不高的場合。重心法則是以隸屬度函數曲線與橫坐標圍成的面積的重心作為輸出值，能夠得到更準確的控制量。加權平均法廣泛應用于工業控制中，根據系數的選擇決定系統具有不同的響應特征。本文選用重心法計算模糊推理的最終輸出值，計算公式為

(3)

將推論結果的隸屬度函數代入式(3)進行解模糊，得到輸出量Step=1.4 m，Angle=0.6 rad。

2 局部死鎖問題的逃脫策略

模糊控制模擬駕駛車輛出現的各種反應設置模糊規則，但當遇到障礙物對稱或大片連續的障礙物，如U型障礙物和一字型障礙物時，會出現局部震蕩也就是死鎖的現象。本文針對復雜障礙物環境提出了障礙逃脫策略，算法流程如圖6所示。

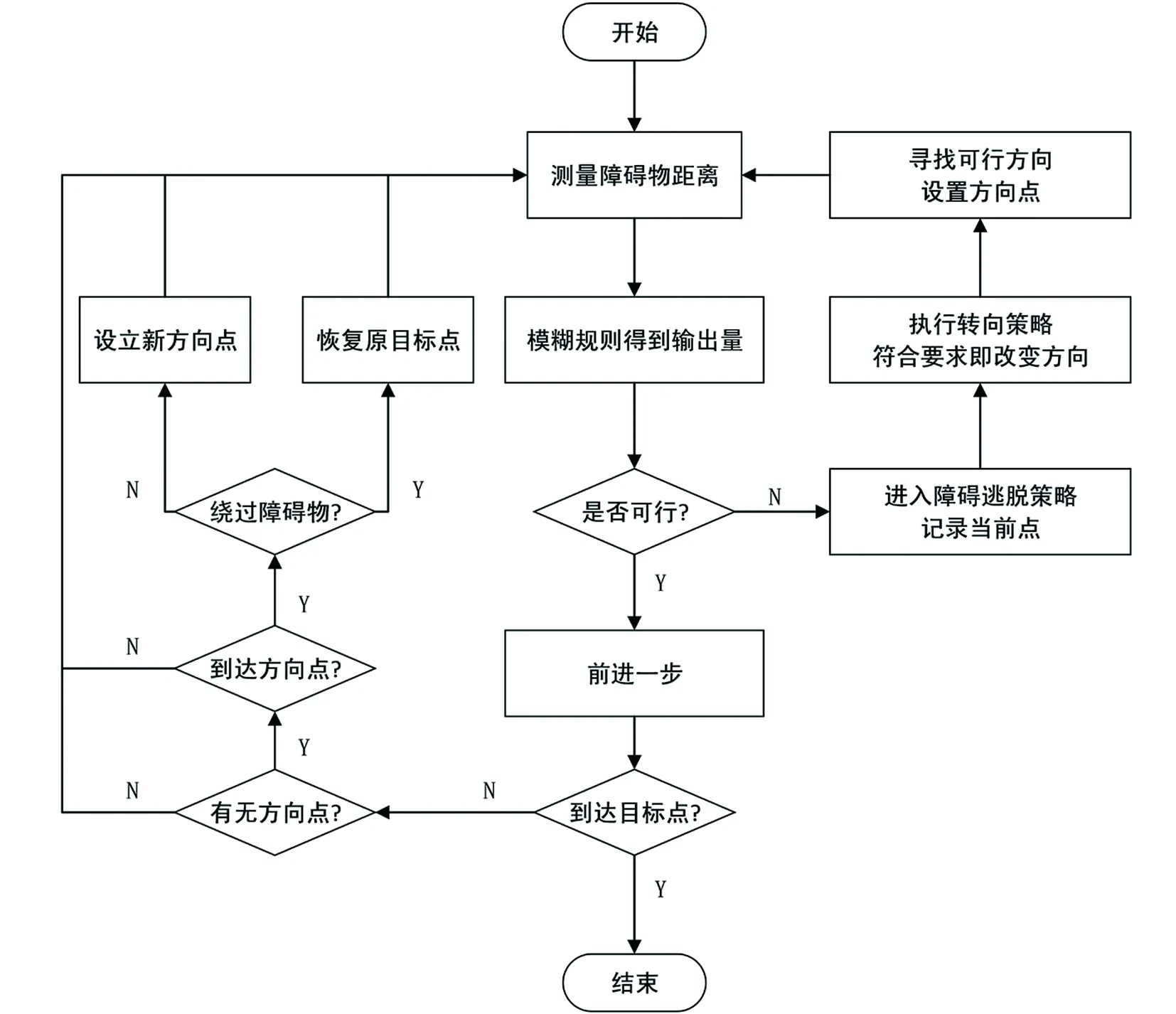
圖6 障礙逃脫策略算法流程Fig.6 Flow chart of obstacle escape strategy algorithm

2.1 障礙逃脫策略

在機器人朝目標點方向行駛的過程中，當遇到小物體的障礙時，根據制定的模糊規則基本能夠找到無碰撞的最優路徑。當遇到連續復雜的障礙環境，根據模糊規則不能走出障礙陷阱區時，進入障礙逃脫策略。

判斷進入逃脫策略的方法：當機器人距離目標點非常近，通過模糊規則得到的輸出量在轉角方向的步長已經大于在此方向上距障礙物的安全距離，就進入障礙逃脫狀態。

根據進入逃脫狀態前左右距障礙物距離dL和dR的比較，選定轉動方向，設置轉動方向標志JudgeTurn，JudgeTurn的計算公式為

(4)

以圖7所示情境為例，dR大于dL，選擇初始轉動方向為右。機器人向右偏轉一定角度θr直到前方距障礙物距離可行。設置初始偏轉角度θr=0，每次循環累加固定角度及隨機擾動值ε，預防陷入死循環，θr的計算公式為

(5)

圖7 逃脫過程示意圖Fig.7 Schematic diagram of escape process

在此方向上設立方向點，暫時將方向點代替目標點，讓機器人繼續沿障礙物邊緣前行。以圖7中方向點1為例，在F點向右偏轉，當偏轉到θr角度時，在此方向上探測不到障礙物，設置方向點1暫時代替目標點，機器人朝向方向點1前行。

當機器人到達方向點時，測量當前位置到目標點方向向右一定范圍(例如120°)內有無障礙物，如圖7中黃色扇形區域。若有障礙物，則在當前位置到目標點方向向右120°方向上設立新的方向點，沿新方向點前行；若沒有障礙物，則判斷走出了障礙范圍，機器人將繼續沿目標點方向前行。

2.2 改變轉動方向策略

若障礙物環境是復雜又近似封閉的，在進入障礙逃脫狀態后，很難準確判斷是否走出整個障礙環境，由于初始轉動方向確定后若隨意改變易出現回退現象，若始終保持不變則容易在局部范圍出現路徑往復現象，而初始轉動方向可能不是得到最優路徑的選擇。為了能使機器人盡可能不走回頭路地到達目標點，要找到適合改變轉動方向的時機。

每當下一步不可行并且指向目標點時，記錄當前點，當再次到達記錄點并且仍指向目標點時，改變初始轉動方向。

添加了改變轉動方向的行為后，在復雜的障礙物環境中，基本能夠最終到達目標點，但由于視野的局限性，得到的路徑并不一定最優。

3 模糊控制路徑規劃的仿真結果

在MATLAB R2016平臺上，對本文提出的算法進行了仿真驗證。圖8是在各種障礙物環境下得到的路徑規劃仿真結果。仿真環境大小是100×100，“*”代表起始點，“?”代表目標點，黑色區域代表障礙物。

圖8(a)所示，在障礙物成離散分布的一般環境中，僅使用模糊規則就能找到最優路徑。圖8(b)和(e)所示，當運動到距障礙物很近的狀態下，探測到右邊到障礙物的距離大于左邊的，選擇向右轉向，沿邊走出障礙物，朝向目標點繼續前進。圖8(c)所示，探測到左邊到障礙物的距離大于右邊的，選擇向左轉向，沿邊走出障礙物。圖8(d)所示，當采取障礙逃脫策略運動到封閉環境的出口處時，探測到走出障礙物，朝向目標點前進，當再次運動到距障礙物很近的狀態下，依然選擇第一次進入逃脫狀態的逃脫方向，直至走出障礙物。本文的模糊控制規則和障礙逃脫策略能夠較好地找到從起始點到達目標點的較優路徑。但由于機器人運動時探測距離的局限性，在進入障礙逃脫策略時根據左右探測距離的遠近決定逃脫方向，如圖8(f)所示，機器人在進入障礙逃脫策略時選擇右轉逃脫成功到達目標點。若在進入障礙逃脫策略時選擇左轉逃脫，則易困在障礙物內，出現路徑往復的現象，無法到達目標點，如圖9所示。加入了轉向策略后，如圖10所示，機器人能在第二次經過記錄點時改變轉向方向， 順利到達目標點，雖然得到的結果經過了一段不必要的路徑，但由于探測距離和對周圍信息的感知有限，機器人在復雜環境中邊探測邊行走，能夠不走回頭路地到達目標點，達到了本文算法的預期。

(a)一般環境 (b)一字型障礙物

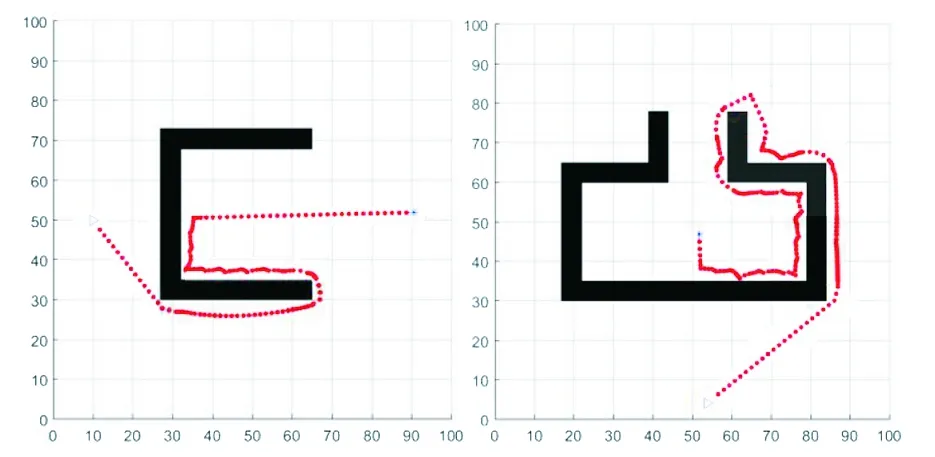
(c)U型障礙物 (d)近似封閉環境

(e)L型障礙物 (f)復雜環境圖8 各種障礙物環境下的路徑規劃Fig.8 Path planning in various obstacle environments

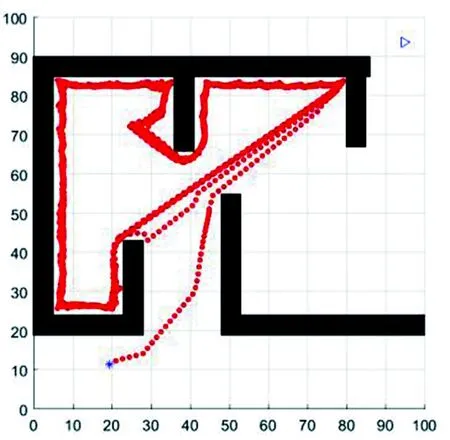
圖9 未使用轉向策略Fig.9 Path planning without steering policy

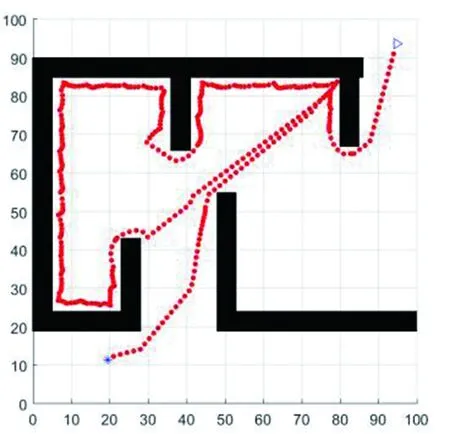
圖10 使用轉向策略Fig.10 Path planning with steering strategy

4 結論

本文采用模糊控制的方法，加入了逃脫策略和轉向策略解決模糊控制中易出現的死鎖問題。在MATLAB R2016平臺上使用本文算法進行仿真。仿真結果表明，在一般復雜環境中，能夠規劃出從起始點到目標點無碰撞的較優路徑；在較封閉的復雜環境中，也能夠規劃出可行路徑到達目標點。本文算法還存在路徑冗余和不平滑的問題，解決這一問題可以嘗試結合其他智能算法，使得能夠更早地判斷即將進入陷阱區，優化路徑。