磁通e-HR神經元模型的Hopf分岔分析與控制

王紅梅，安新磊，喬 帥，張 薇，楊天宇

(1.蘭州交通大學 數理學院，甘肅 蘭州 730070； 2.北京交通大學 電子工程學院，北京 100044)

神經元是生物神經系統的基本結構單元，是神經系統的重要組成部分，在調節神經元系統的動態行為中起著舉足輕重的作用。其活動主要表現為生物電信號的形成、變化和傳遞。生物神經系統是一個復雜的多層次信息神經網絡，是通過大量神經細胞的連接形成的。因此，在神經元發射和信息編碼過程中，涉及到復雜的非線性動力學行為。由于神經元動力學是生物生理學和非線性動力學之間的交叉學科，因此研究神經元的發射具有生物學和動力學意義。隨著生物生理學和非線性動力學理論的不斷發展，基于不同研究周期的數據建立了各種與生物神經元相關的模型[1]。據我們所知，作為一個數學神經元模型，三個變量的HR神經元模型不能描述離子通道的作用。因此，一些研究者提出了四變量的HR神經元模型[2]，該模型可以更好地描述神經元的動態行為，并可通過實驗結果驗證[3]。

由于神經元系統中的神經元處于復雜的狀態，神經元的電活動過于復雜，需要考慮更多的因素。例如，根據法拉第感應定律，神經元中的動作電位的變化可以在介質中產生磁場。通過分析文獻[4]可知，神經元的各種放電活動是通過信號的傳遞完成的，它們因為受電磁場的影響，所以在電磁輻射下可以產生不同的放電狀態，如靜息態、尖峰放電、簇放電[5]。文獻[6]討論的是HR神經元模型的Hopf分岔分析及穩定性分析；文獻[7]用Washout控制器對Morris-Lecar(ML)模型進行Hopf分岔控制；文獻[8-15]討論神經元模型的分岔分析及其存在的隱藏吸引子，并對神經元模型的分岔進行控制。神經元的放電模式極其豐富，故有必要對神經元模型進行深入研究。

研究發現，磁通e-HR神經元模型具有豐富的分岔行為和放電特征。數值模擬分析了當外界刺激電流變化情況下系統的平衡點分布與穩定性分析，并且得出該模型存在亞臨界Hopf分岔點。通過數值仿真表明，當系統發生亞臨界Hopf分岔時，隨著初值的不同，神經元會表現為不同的放電特性。另外，利用Washout分岔控制器對分岔點的分岔類型進行控制，將亞臨界Hopf分岔轉化為超臨界Hopf分岔，從而實現消除膜電壓隱藏放電的目的。

1 模型描述

描述神經元模型分岔分析時最常用的模型是Hindmarsh-Rose(HR)神經元模型，但是也有另外一種模型，e-Hindmarsh-Rose(e-HR)神經元模型[16]，它具有和HR神經元模型相似的特性。所以，基于e-HR神經元模型，考慮外界電磁場對膜電位變化的影響，引入磁通量后建立的e-HR神經元模型的微分方程如下：

(1)

式中：a,b,c,d,e,f,g,u,s,h,v,k,r,L表示系統的參數；變量x表示神經元的細胞膜電位；y表示快電流；z表示自適應電流；w表示緩慢的動力學過程；φ表示穿過神經元細胞膜的磁通量；I表示的是外部刺激電流；W(φ)是由磁通量控制憶阻器的記憶電導[4]，它的表達式可以寫為W(φ)=α+3βφ2；此文中的各個參數取值如下：a=1,b=3,c=1,r=3,L=1.619,k0=0.1，d=0.99,e=1.01,s=3.966,k=0.957 3,v=0.000 9,k1=0.9,k2=0.5,β=0.02,f=5.012 8 ，g=0.027 8,u=0.002 15,h=1.605,α=0.1。

2 平衡點的分布

神經元的不同放電模式和平衡點的分布都與它的類型有關，對于模型(1)而言，它的平衡點可以由其動力學方程確定，令x'=0,y'=0,z'=0,w'=0,φ'=0，得到對應的零線方程：

(2)

方程(2)中各個式子的交點就是系統(1)的平衡點，由方程(2)可以得到細胞膜的總電流方程[6]如下：

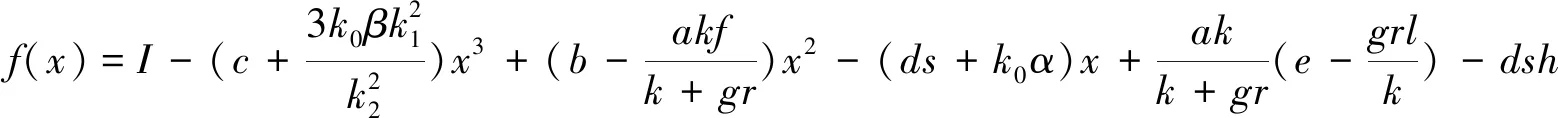
(3)

將各參數帶入式(3)中得：

f(x)=I-1.019 440x3-1.611 082x2-3.936 34x-5.502 459=0

(4)

IH=0.843 392μA/cm2，pH=(-1.305 042,-7.053 972,1.189 635,-17.032 191,-2.349 075)，

通過上述分析得出，系統(1)在平衡點pH處有一對實部為零的共軛特征根，因此可知系統(1)在分岔點H處發生了Hopf分岔。

(a)系統(1)平衡點曲線與Hopf分岔點 (b)特征根隨外部刺激電流的變化曲線圖1 系統隨外界刺激電流變化時的兩類曲線Fig.1 Two types of curves of the system as a function of external stimulus current

3 Hopf分岔類型的判定

對一些高維的非線性系統來說，求解特征根較繁瑣，可用一種較為簡便的方法求解特征多項式的根，以此來判定Hopf分岔的類型及其穩定性，從而簡化高維系統的計算，較為簡便。

令系統(1)為

X'=F(x)

(5)

式(5)中：

下步判斷系統(5)在平衡點pH=(-1.305 042,-7.053 972,1.1896 35,-17.032 191,-2.349 075)處的Hopf分岔類型，此時的外界刺激電流I=0.843 392 μA/cm2，在平衡點pH處的線性化矩陣為

矩陣ApH的特征根為

144。

將系統(5)的線性部分提出改寫為：

X′=F(X)=ApHX+G(X)

(6)

則:

X'=PY'=ApH(PY+pH)+(PY+pH)

(7)

從而:

(8)

按照Hopf分岔理論可得Hopf分岔穩定性判別式為

(9)

穩定性指標ηH決定Hopf分岔周期解的穩定性，當ηH<0或者(ηH>0)時，系統(5)分岔產生的周期解是穩定(不穩定)的，即系統發生了超臨界Hopf分岔(亞臨界Hopf分岔)，也就是分岔周期解的周期是增加(減小的)，判別式(9)中各個量的相關計算表達式為：

通過計算可知，穩定性指標ηH=0.055 92>0，因此可知系統(1)在平衡點pH發生了亞臨界Hopf分岔，從而在分岔點H前后系統(1)的穩定性發生了改變，由不穩定態變為穩定狀態，并且系統(1)會產生不穩定的極限環。

4 數值模擬

通過上述理論分析可知，當外界刺激電流為IH時，系統(1)在平衡點pH發生亞臨界Hopf分岔，從而使膜電壓x的放電特性發生變化，因此有必要分析系統(1)在Hopf分岔點H附近的放電特性。當外界刺激電流為I1=0.83 μA/cm2時，此時系統的平衡點為：q=(-1.307 749,-7.110 632,1.178 898,-16.269 609,-2.353 948)，在該平衡點處線性矩特征根

所以平衡點q是穩定的結焦點。

當外界刺激電流為I1，初值為(-2.307 749,-7.110 632,1.178 898,-16.269 609,-2.353 948)時，系統(1)膜電壓x的時間響應圖和相軌跡如圖2(a)、(b)所示，此時的膜電壓x為穩定的靜息態。當外界刺激電流I1保持不變，取初值為(-5.307 749,-7.110 632,1.178 898,-16.269 609,-2.353 948)時，系統(1)的膜電壓x的時間序列圖和相軌跡如圖2(c)、(d)所示，此時膜電壓x是周期為2的尖峰放電狀態，它的相軌跡為穩定的極限環。由此可知，當外界刺激電流I1保持不變時，初值取值不同，系統(1)的放電模式也會不同，并且產生了隱藏放電現象。

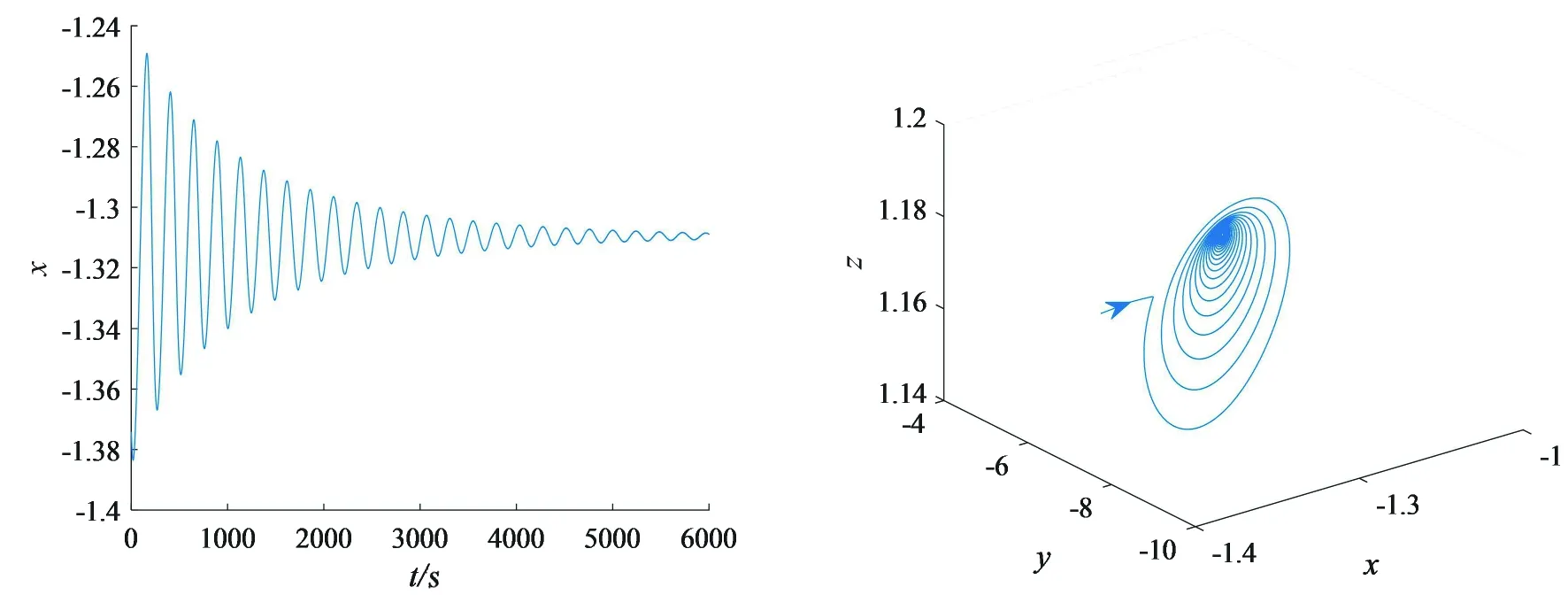
(a)膜電壓x的時間序列圖 (b)相軌跡

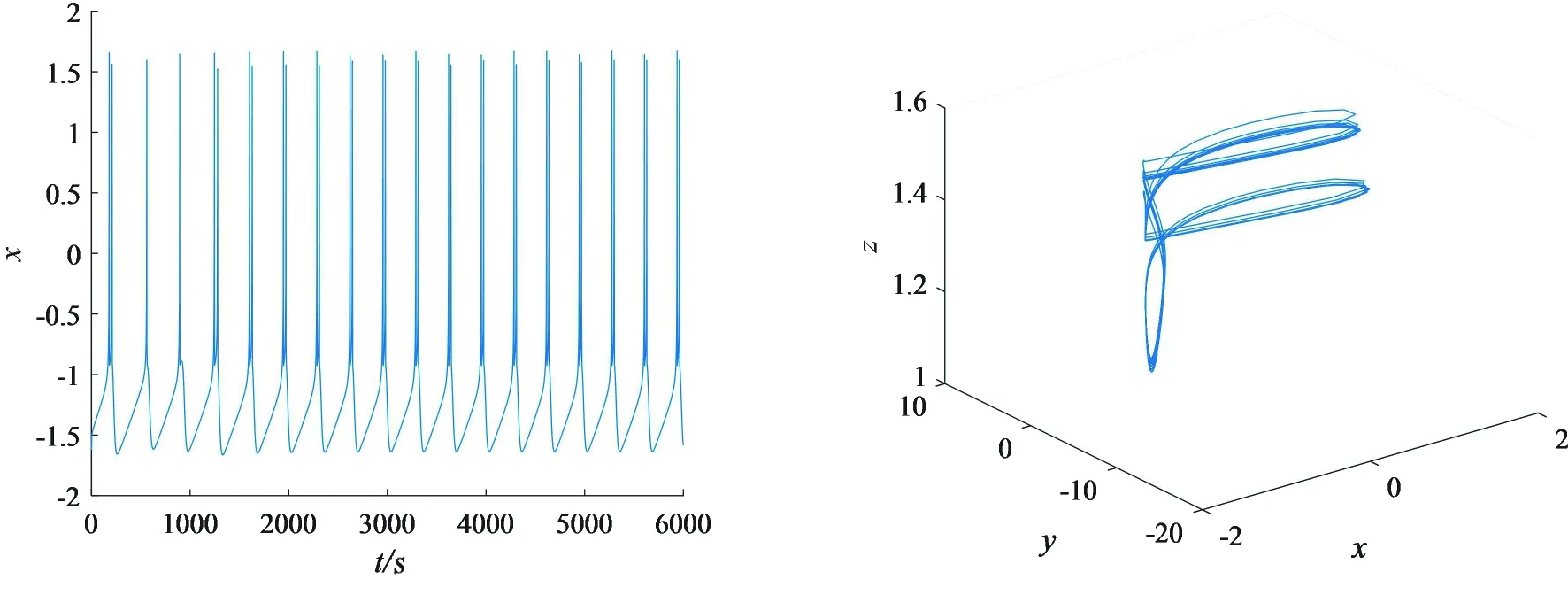
(c)膜電壓x的時間序列圖 (d)相軌跡圖2 系統(1)的放電分析Fig. 2 Discharge analysis of system (1)

系統(1)在平衡點q處的隱藏動力學行為如圖3所示。圖3中黑星表示平衡點q；紅色區域表示穩定平衡點的吸引域，此時膜電壓x處于靜息態；藍色區域表示隱藏吸引子吸引域，此時膜電壓處于周期為2的尖峰放電。當外界刺激電流為I1時，系統(1)對于不同的初始狀態有著不同的放電特性，從而揭示了神經元模型在發生亞臨界Hopf分岔時，在平衡點q處產生了隱藏放電現象。因為與神經元相關的各種疾病都是由于神經元發生異常而引起的，所以控制系統(1)的隱藏放電行為具有很重要的實際意義。

5 隱藏動力學控制

由于系統(1)在分岔點H處發生亞臨界Hopf分岔，并且在其附近發現隱藏的極限環吸引子，使神經元膜電壓產生隱藏放電行為。本小節基于Washout分岔控制器，對分岔點H的Hopf分岔類型進行控制，在不改變平衡點pH位置的前提下，使其亞臨界Hopf分岔轉化為超臨界Hopf分岔，從而使系統(1)在分岔點H處附近的拓撲結構發生改變，由此達到消除膜電壓隱藏放電的目的，施加控制后的神經元系統如(10)所示。

(10)

受控系統(10)中的v為Washout濾波器的狀態變量，n為控制器的反饋增益，ξ為濾波器時間常數的倒數。當ξ<0時為不穩定的Washout控制器；當ξ>0時為穩定的Washout控制器，因此選取ξ=-0.035，其余參數取值與系統(1)參數取值一樣，u=n(x+ξv)3,W(φ)=α+3βφ2。

當外界刺激電流I1=0.83 μA/cm2時，此時受控系統(10)的平衡點為:q'=(q,v')=(-1.307 749,-7.110 632,1.178 898,-16.269 609,-2.353 948,-37.364 256)，通過數值仿真發現，當反饋增益n<-0.377 8時，不管膜電壓取何值，受控系統(10)的隱藏放電行為完全消失，反饋增益n對受控系統(10)的隱藏放電的影響如圖4所示。圖4中藍色區域表示穩定的吸引域，此時受控系統(10)膜電壓x處于靜息態；紅色區域表示隱藏的吸引子，此時受控系統(10)膜電壓處于周期為2的尖峰放電；黑星表示受控系統(10)的平衡點。

圖3 系統(1)在平衡點q處的隱藏放電區域分析Fig. 3 Analysis of hidden discharge area at equilibrium point q in system (1)圖4 反饋增益n對受控系統(10)膜電壓x的放電影響Fig. 4 Effect of feedback gain (n)on discharge voltage of controlled system (10) membrane (x)

6 結論

基于理論分析與數值仿真相結合的方法發現，當外界刺激電流I1保持不變時，取不同的初值，系統(1)的放電模式也會不同。通過引入磁通量來分析e-HR神經元模型的分岔分析與平衡點的分布及穩定性可知，系統(1)存在一個分岔點H，且在分岔點H處發生亞臨界Hopf分岔，并且在它的附近發現了隱藏的極限環吸引子。運用Washout分岔控制器，對分岔點H進行Hopf分岔控制，使其亞臨界Hopf分岔轉化為超臨界Hopf分岔，從而實現消除膜電壓隱藏放電的目的。研究結果有助于探究和控制神經元的隱藏放電行為。