重型車輛主動懸架的滑模控制器設計及優化
高坤明,郭宗和,于瑤瑤,于慧,張裕晨
(1.山東理工大學 交通與車輛工程學院, 山東 淄博 255049;2. 山東理工大學 材料科學與工程學院, 山東 淄博255049)
重型車輛工作環境相對較差,乘員駕駛時間較長,貨物裝載的重量較大,因此對車輛的性能具有更高的要求。近年來,學者們對重型車輛的研究逐步深入[1-4]。傳統被動懸架因無法改變懸架剛度和阻尼,很難滿足重型車輛的行駛要求。與被動懸架相比,主動懸架能夠處于最佳減振狀態,對進一步提高重型車輛性能起著重要的作用,目前,許多專家和學者致力于主動懸架的設計和優化[5-7]。主動懸架發揮良好性能的關鍵是具有合適有效的控制策略,其中滑模控制對于處理模型的不確定性、系統的非線性和外部擾動具有較強的魯棒性,已被廣泛應用于主動懸架的控制中[8-9]。能否處理好主動懸架優化過程中多個目標的矛盾是優化結果好壞的關鍵,針對這一問題,多目標優化方法在懸架的優化中顯得特別重要[10-12]。
為進一步提高重型車輛的性能,本文基于四自由度1/2主動懸架模型,利用滑模控制方法對主動懸架進行控制器設計,結合遺傳算法對滑模控制器參數進行多目標優化,研究優化前后路面激勵響應下主動懸架系統的魯棒性。
1 主動懸架系統模型
本文建立了四自由度振動的1/2車輛懸架系統模型,如圖1所示。圖1中,ms、mt1和mt2分別為1/2車身質量和前后車輪質量,θ為車身質心處俯仰角位移,IS為車身俯仰轉動慣量,a和b分別為質心到前、后軸的距離,xs、xs1和xs2分別為車身質心處垂直位移和前后懸架垂直位移,ks1、ks2、cs1和cs2分別為前后懸架的彈簧剛度和阻尼,xt1和xt2分別為前后車輪垂直位移,kt1、kt2、ct1和ct2分別為前后輪胎等效剛度和阻尼,xr1和xr2分別為前后車輪隨機路面激勵,u1和u2分別為前后懸架控制器控制力。

圖1 四自由度1/2車輛模型Fig.1 The 4-DOF model of 1/2 vehicle body
根據牛頓第二定律可建立懸架系統的微分方程,即
(1)
由于車身俯仰角一般較小,因此前后懸架垂直位移可以表示為
xs1=xs+aθ,xs2=xs-bθ
(2)
將式(1)中第1個式子與a和b分別相乘且與第2個式子相加減,并將式(2)帶入其中整理可以求得
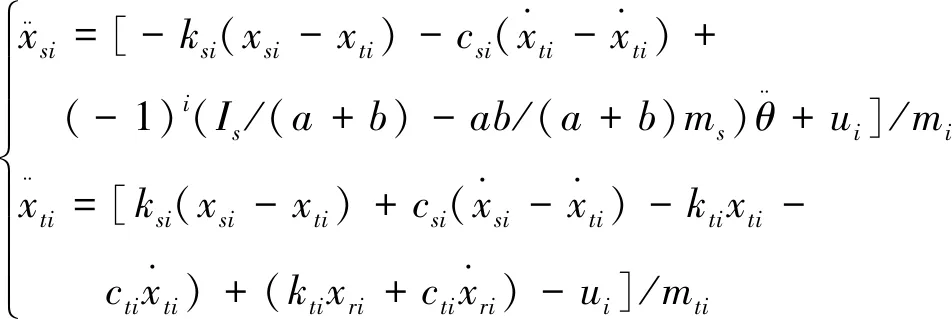
(3)
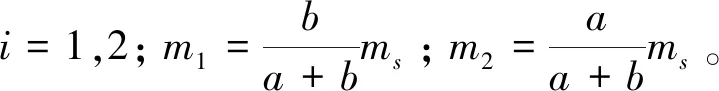
將懸架系統模型中的狀態變量定義為
X=[xa1,xa2,xa3,xa4,x5,xb1,xb2,xb3,xb4]T
(4)

(5)
由狀態變量可以得到系統的狀態方程為
(6)
2 滑模控制器設計
對于四自由度1/2車輛主動懸架多輸入多輸出系統,滑模控制的切換函數為
(7)
式中,λa1、μa1、λa2、μa2和λb1、μb1、λb2、μb2為滑模面參數。
定義系統狀態的跟蹤誤差為
(8)
式中:i=1,3;xaid和xbid分別為xai和xbi期望參考軌跡。
(9)
式中:
fa1=-ks1(xa1-xa3)-cs1(xa2-xa4)
fa2=ks1(xa1-xa3)+cs1(xa2-xa4)-kt1xa3-ct1xa4)
fb1=-ks2(xb1-xb3)-cs1(xb2-xb4)
fb2=ks2(xb1-xb3)+cs2(xb2-xb4)-kt2xb3-ct2xb4
ρad=λa1xa1d+μa1xa2d+λa2xa3d+μa2xa4d
ρbd=λb1xb1d+μb1xb2d+λb2xb3d+μb2xb4d
根據式(9)可以求得等效控制輸入為
(10)
等效控制器要求系統具有精確模型且不存在外界干擾,然而實際系統存在不確定性的路面干擾,導致系統不能單純由等效控制器進行控制,為克服系統不確定性的影響,引入以下切換控制律
(11)
由式(10)和式(11)可以得到用于控制實際系統的實時可變的滑模控制力,即
(12)
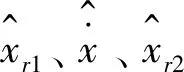
(13)
式中,Fa1、Fa2和Fb1、Fb2分別為前后車輪路面函數和前后車輪路面函數導數的極值。
為了使設計的控制律能保證系統在任意初始狀態都能到達滑模面,即滿足滑模控制的到達條件,利用Lyapunov穩定性理論對滑模控制進行穩定性驗證,選取Lyapunov候選函數為
(14)
將式(14)對時間t求導,當Ka和Kb滿足
(15)

為了避免高頻振動,在實際控制中,用飽和函數sat(s(t),φ)取代符號函數sign(s),飽和函數公式如下:
(16)
式中,0<φ<1為開關控制項的邊界層厚度。
3 多目標設計優化
3.1 目標函數選擇
對于重型車輛而言,復雜的路面條件和重型的貨物載荷是破壞車輛乘坐舒適性、操縱穩定性以及貨物完整性的重要因素,長期顛簸和不舒適的駕駛環境會對駕駛員造成身體上和心理上的傷害,同時車輪跳動和車身俯仰運動會造成車輛的操縱穩定性變差,貨物完整性降低。綜合考慮車輛乘坐舒適性、操縱穩定性以及貨物完整性因素,以車身質心處垂直加速度為車輛乘坐舒適性目標,以前后輪胎動位移為車輛操縱穩定性目標,以車身俯仰角加速度為貨物完整性目標,目標函數如下:
(17)
式中,f1、f2、f3和f4分別為車身質心處垂直加速度均方根值、前輪胎動位移均方根值、后輪胎動位移均方根值和車身俯仰角加速度均方根值。
3.2 約束條件
1)為保證行駛過程中車輛和貨物的安全性,前后懸架動行程要在動撓度的范圍內避免限位機構的撞擊,即
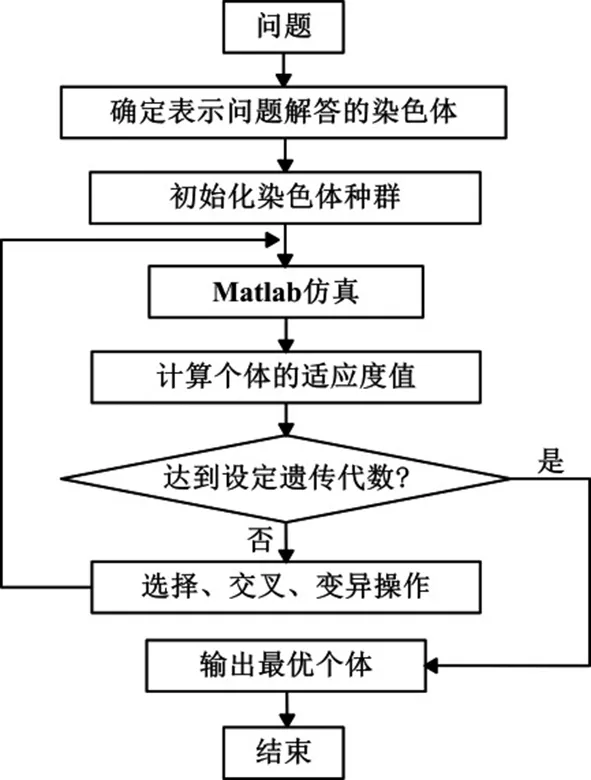
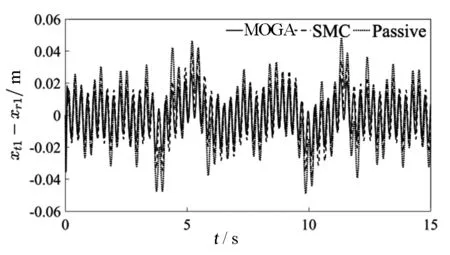
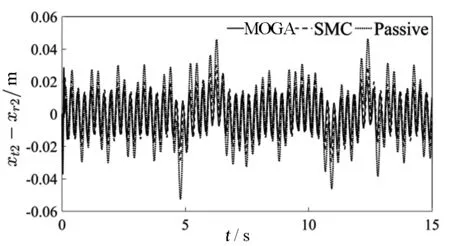
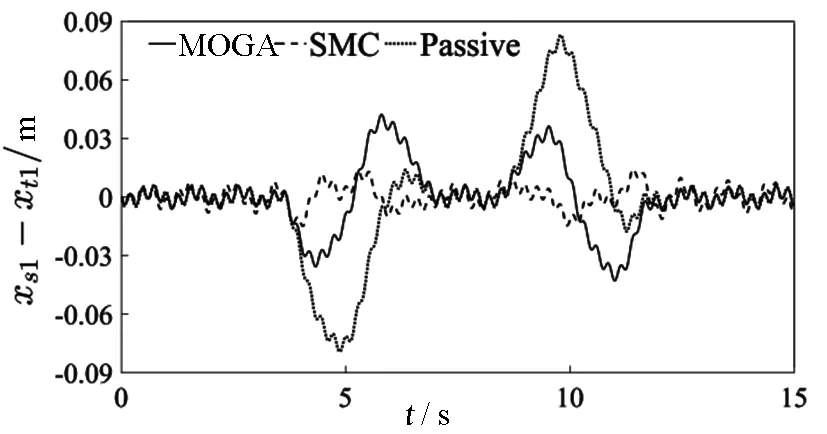
xs1-xt1 (18) 式中,xR為允許的最大懸架動撓度。 2)為保證控制器能夠始終在正常狀態下工作,要求控制器輸出的控制力應小于主動懸架控制器的最大輸出力,即 u1 (19) 式中,Fmax為允許的控制器最大輸出力 多目標優化是多準則決策的一個領域,即涉及多個目標的數學問題的同時優化。由主動懸架數學模型可知,主動懸架設計優化的實質是具有多個變量及各類約束的優化問題,控制性能以及穩定性由控制器中的12個參數K=[λa1,μa1,λa2,μa2,η1,φ1,λb1,μb1,λb2,μb2,η2,φ2]所決定,通過選擇這些參數的取值來滿足4個目標以及約束條件,同時通過滑模控制器的參數可以將多目標優化設計問題寫成以下函數: (20) 式中:F為由目標函數組成的映射;K∈Q是一個12維的設計參數向量。式(20)是多目標設計問題數學模型的一般形式,利用基于Pareto最優的多目標優化方法對優化問題進行求解,最終從多目標優化解集中選取一組相對最優的滑模控制器參數進行實例仿真。 Q={K∈R12|g(K)>0} (21) 式中,約束條件g(K)>0由不等式(18)和(19)組成。 合適的適應度函數可以顯著增加算法的收斂速度。各目標函數值滿足約束條件下盡可能小是主動懸架優化問題所要實現的,所以直接將多目標函數轉化為適應度函數即可獲得較好的效果,適應度函數可表示為 Fit(K)=min[f1,f2,f3,f4]T (22) 在確定適應度函數和約束條件后,結合遺傳算法可以輸出最優個體。遺傳算法將問題參數編碼為染色體,然后通過迭代過程實現選擇、交叉和變異,不斷更新新的個體和種群,最終獲得滿足優化目標的染色體,整個優化程序的流程如圖2所示。 圖2 遺傳算法優化流程Fig.2 Process of genetic algorithm optimization 1)染色體編碼 將優化模型的12個變量依次連接成編碼串,每個編碼串代表種群中的1個個體,每一個個體都是可行解,初始種群數量設為200。 2)選擇、交叉和變異 選擇是為了從當前迭代群體中找到更加優秀的個體,并且使這些個體有更大的幾率遺傳到下一代,選擇概率設定為0.9。 交叉是將優秀的個體進行結合,使其在迭代過程中能夠更大概率地產生優秀個體,交叉概率設定為0.8。 變異可以保證種群的多樣性,通過變異能夠生成不同于父輩的新的個體,變異概率設定為0.01。 3)終止條件 終止條件是用于實現遺傳算法迭代終止的條件,通過終止條件,算法程序自動停止,并輸出結束時的最優解,最大迭代次數設為300代。 在仿真過程中,初定參數K的取值范圍如下: (23) 為驗證所設計滑模控制器的正確性以及多目標優化方法的有效性,基于已建立的懸架模型和穩定性條件進行實例仿真驗證,其中所用到的某重型車輛模型參數如下: ms=6 900 kg,Is=31 200 kg·m2, mt1=380 kg,mt2=640 kg,ks1=320 000 N/m, ks2=570 000 N/m,cs1=14 500 N·s/m, cs2=22 000 N·s/m,kt1=890 000 N/m, kt2=1 900 000 N/m,ct1=1 700 N·s/m, ct1=3 200 N·s/m,a=3.1 m,b=1.3 m, xR=0.08 m,F=2 000 N。 仿真過程中所使用的路面激勵如下: (24) 式中,d(t)=0.002sin2πt+0.002sin7.5πt。 假設車輛以15 km/h的速度直線行駛,則前后車輪相隔1.06 s的時間經過相同的路面,即前后車輪所經過的路面激勵都可以由路面激勵函數(24)來表示。 根據已建立的模型和優化控制算法,在上述路面激勵下進行Matlab仿真,將優化后的主動懸架與優化前的主動懸架及被動懸架進行對比。表1為優化前后滑模控制器參數,圖3—圖6分別為優化后的重型車輛主動懸架與優化前的主動懸架及被動懸架車身質心垂直加速度、前后懸架輪胎動位移和車身俯仰角加速度均方根值的對比曲線。表2為優化前后及被動懸架各目標函數值,圖7和8分別為優化前后主動懸架及被動懸架前后懸架動行程均方根值對比曲線,圖9為優化前后主動懸架控制器控制力對比曲線。 表1 優化前后滑模控制器參數 參數λa1μa1λa2μa2η1?1λb1μb1λb2λb2η2?2SMC7504150.4245050015300.510030MOGA4 987.669 553614.7354.41 156.3698.15 762.87 434.6544.6370.51 433.2785.3 圖3 車身質心垂直加速度對比曲線Fig.3 Vertical acceleration curve of the vehicle body 圖4 前懸架輪胎動位移對比曲線Fig.4 Tire dynamic displacement curve of front suspension 圖5 后懸架輪胎動位移對比曲線Fig.5 Tire dynamic displacement curve of rear suspension 從圖3—圖6可以看出,多目標遺傳算法優化后的重型車輛主動懸架車身垂直加速度均方根值、前后輪胎動位移均方根值和俯仰角加速度均方根值明顯小于優化前主動懸架及被動懸架的對應值。從表2可以計算出,與被動懸架及優化前的主動懸架相比,利用多目標遺傳算法優化后的重型車輛主動懸架車身垂直加速度均方根值與優化前的主動懸架及被動懸架對應值分別減小了53.4%和33.7.4%,極大改善了重型車輛的乘坐舒適性;前懸架輪胎動位移均方根值分別減少了38.7%和9.5%,后懸架輪胎動位移均方根值分別減少了43.7%和10.0%,有效增強了重型車輛的抓地能力,提高了操縱穩定性;俯仰角加速度均方根值分別降低了54.8%和35.6%,有效提高了重型車輛操縱穩定性和保持貨物完整性的能力。 圖6 俯仰角加速度對比曲線Fig.6 Pitch angle acceleration contrast curve 表2 仿真結果 目標值f1/(m·s-2)f2/mf3/mf4/(rad·s-2)Passive 0.3830.0310.0320.124SMC0.2610.0210.0200.087MOGA0.1730.0190.0180.056 圖7 前懸架動行程對比曲線Fig.7 Dynamic travel contrast curve of front suspension 圖8 后懸架動行程對比曲線Fig.8 Dynamic travel contrast curve of rear suspension 圖9 控制器控制力對比曲線Fig.9 Controller control force contrast curve 從圖7和圖8中可以看出,被動懸架的重型車輛在經過不平路面時,當前后懸架動行程的最大值達到懸架動撓度的極限,會引起阻尼器及限位機構發生撞擊,造成機構的破壞,同時不利于車輛的舒適性。優化后重型車輛主動懸架的前后懸架動行程始終在動撓度范圍內,滿足約束條件。但從仿真結果又可以看出,優化后4個目標函數得到大幅度改善的同時,前后懸架動行程與優化前主動懸架動行程相比,在最大動撓度極限范圍內出現了略幅增大,說明在優化過程中犧牲了一定的懸架動行程從而達到了優化的目的。 從圖9中可以看出,優化前的主動懸架控制器控制力最大值超出了主動懸架控制器的最大輸出力,這是機構不能夠實現的,而優化后的主動懸架控制器控制力始終保持在控制器輸出力極限值內,且最大控制力在1 000 N左右,這是比較容易實現的。 本文建立了四自由度1/2重型車輛主動懸架模型并實現了系統的解耦,結合滑模控制方法對主動懸架進行了滑模控制器的設計,利用Lyapunov穩定性理論對控制器進行穩定性驗證。以前后懸架動行程、控制器控制力輸出為約束條件,以車身質心垂直加速度、前后懸架輪胎動位移以及俯仰角加速度為控制目標,對滑模控制器參數進行了多目標遺傳算法優化,彌補了按經驗選取控制器參數的不足。結合實例仿真驗證了基于多目標遺傳算法優化的重型車輛主動懸架滑模控制方法的有效性,優化后在約束條件下,車身垂直加速度、前后輪胎動位移和俯仰角加速度目標值均有一定程度的減小,為主動懸架在重型車輛的進一步應用提供了一定的借鑒。3.3 多目標優化問題的提出
3.4 多目標遺傳優化算法
4 仿真結果分析
Tab.1 Sliding mode controller parameters before and after optimization


Tab.2 Simulation results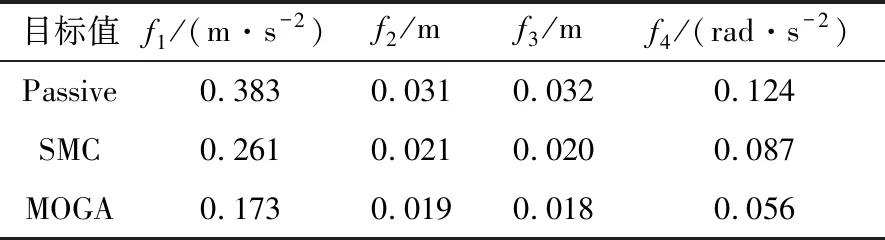


5 結束語

