一道高二數學期考題的解法探究

陜西省漢中市四〇五學校 (723312) 侯有岐

在近年的各類考試中，經常涉及三角形面積及相關問題的最值或取值范圍的問題.此類問題往往前景活潑多樣，難度較大，解決的思維方式多變，解決的方法也多種多樣.因此一直備受命題者的青睞.這里以一道高二考試題為例，探索如何解決此類問題的常見解法，希望有益于大家理解題目的本質，同時注意體會在解題過程中，如何適時實施轉化化歸的方法.

一、試題呈現

題目(2019年洛陽市高二數學考試第12題)

本題通過已知三角形中有關邊長及點的特殊位置，進而求解三角形面積的最大值.解決問題時可以從“數”的角度和“形”的角度兩方面入手，使數與形有機結合，這樣就可以利用多種思想方法完成，從而有助于學生數學學科素養的培養.

二、多解思維

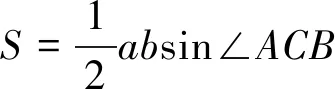
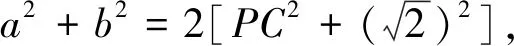
設ab=t(ab≥2)，則y=-3t2+24t-36

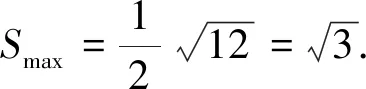
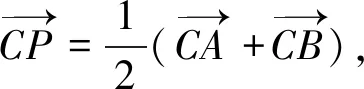
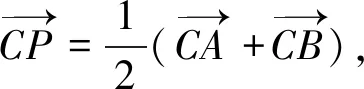
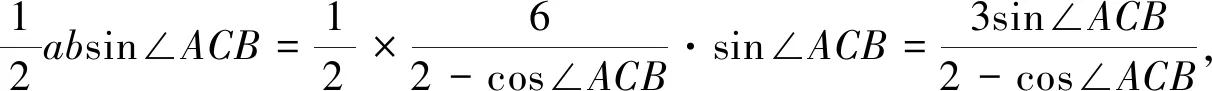
思維角度3：根據已知及“點P是AB的中點”，由三角形中線定理得到a,b的關系式a2+b2=4ab-4，由余弦定理得8=a2+b2-2abcos∠ACB,兩式結合得出6=ab(2-cos∠ACB),再利用系數的轉化與配對并結合不等式(a2-b2)(c2-d2)≤(ac-bd)2(當且僅當bc=ad時取等號)*得出三角形面積的最大值.

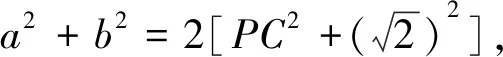
三、解后反思

三角形問題是高考中常考的考點.解決此類問題時，不但要時刻想到正、余弦定理,而且要熟悉三角形的性質和三角函數、向量等有關知識.這類題目一般要求學生會運用數形結合和轉化化歸等數學思想方法從幾何角度來尋找解題途徑，然后通過適當的代數運算加以解決，所以在平時的教學活動中，要指導學生細心審題，認真計算，合理轉化，逐步培養學生思維的創新性，提高學生的數學解題能力.