坐標系與參數方程幾種常見題型的解法

安徽省樅陽縣會宮中學 (246740) 方明生

坐標系與參數方程作為高考的選考內容之一，筆者在高考閱卷中發現，相對于絕對值不等式而言，大部分學生都會選擇坐標系與參數方程的這一題.盡管學生在平時的學習中進行了多次的模擬考試以及大量訓練，但在實際解題過程中依舊會出現障礙.第一問一般考察基本知識，主要涉及參數方程、普通方程和極坐標方程三者間的相互轉化，此問5分學生基本都能夠得到.相對于第一問而言，第二問的得分卻大打折扣，究其原因，主要是學生在解題的過程中沒有完全明白命題老師的意圖，解題的方法不當導致運算量增大或者無從下手，筆者根據近幾年的高考試題，對于第二小問常考題型進行了整理，供各位方家指正.

一、利用直線參數方程t的幾何意義

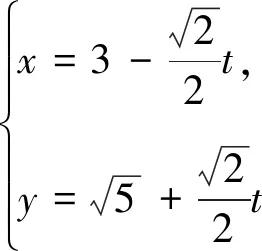
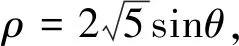
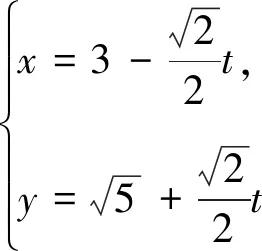
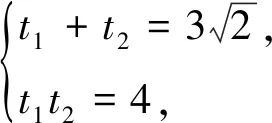
評注：利用極坐標公式ρ2=x2+y2，x=ρcosθ，y=ρsinθ進行化簡即可求出圓c普通方程，再將直線的參數方程代入圓C的直角坐標方程，得到關于參數t的一元二次方程，結合參數t的幾何意義利用根與系數的關系即可求得|PA|+|PB|的值．

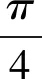
(-2,-4)的點P，且直線l與曲線C相交于A,B兩點.

(1)寫出曲線C的直角坐標方程和直線l的參數方程；

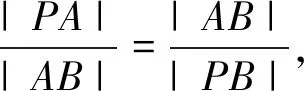
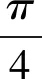
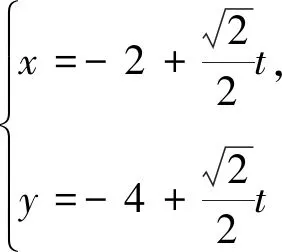
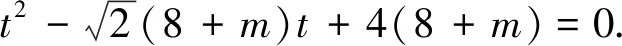
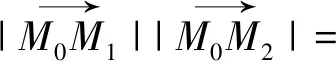
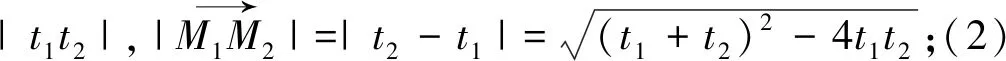
二、利用極坐標ρ的幾何意義

例3 (2017全國Ⅱ)在直角坐標系xOy中，以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C1的極坐標方程為ρcosθ=4．

(1)M為曲線C1上的動點，點P在線段OM上，且滿足|OM|·|OP|=16，求點P的軌跡C2的直角坐標方程；

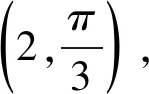
解析：(1)設P的極坐標為(ρ,θ)(ρ>0)，M的極坐標為(ρ1,θ)(ρ1>0)由題設知|OP|=ρ，

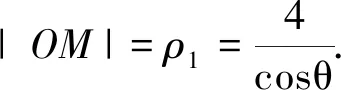
(2)設點B的極坐標為(ρB,α)(ρB>0).由題設知|OA|=2，ρB=4cosα，于是ΔABO面積S=

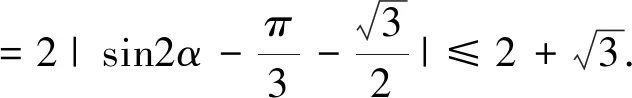
例4 (2016全國Ⅱ)在直角坐標系xOy中，圓C的方程為(x+6)2+y2=25．

(1)以坐標原點為極點，x軸正半軸為極軸建立極坐標系，求C的極坐標方程；

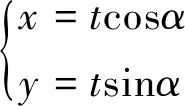
解析:(1)由x=ρcosθ，y=ρsinθ可得C的極坐標方程ρ2+12ρcosθ+11=0.

(2)在(1)中建立的極坐標系中，直線l的極坐標方程為θ=α(ρ∈R).

由A,B所對應的極徑分別為ρ1，ρ2，將l的極坐標方程代入C的極坐標方程得ρ2+12ρcosα+11=0.由韋達定理可得ρ1+ρ2=-12cosα，ρ1ρ2=11.

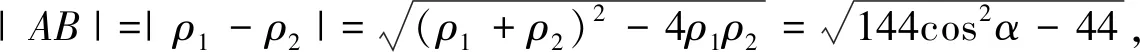
評注:此處所選取的兩個例題均為高考原題，如果大家認真去研究的話會發現它們有共同之處是所給直線為經過原點(即直線的極坐標方程θ=α(ρ∈R))的特殊直線，利用極坐標的幾何意義求解.

三、利用普通方程聯立求解

例5 在直角坐標系xOy中，曲線C1的方程為y=k|x|+2.以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ2+2ρcosθ-3=0.

(1)求C2的直角坐標方程；

(2)若C1與C2有且僅有三個公共點，求C1的方程.

解析:(1)由x=ρcosθ，y=ρsinθ可得C2的直角坐標方程為(x+1)2+y2=4．

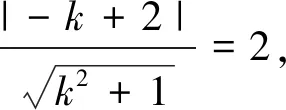
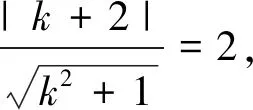
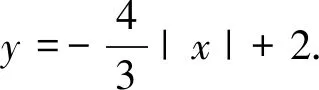
評注:本題明顯不符合前面的兩個題型，對于此類問題，我們都可以用通性通法去解決，借助普通方程進行考查的是有關坐標系與參數方程的問題，涉及到的知識點有曲線的極坐標方程向平面直角坐標方程的轉化以及有關曲線相交交點個數的問題，在解題的過程中，需要明確極坐標和平面直角坐標之間的轉換關系，以及曲線相交交點個數結合圖形，將其轉化為直線與圓的位置關系所對應的需要滿足的條件，從而求得結果.

通過上述三種題型的解答，可以解決坐標系與參數方程問題可以歸納為：“參”代“普”、“極”代“極”、“普”代“普”三種題型，審題的時候要搞清楚出題者的意圖，要學會抓住題干，如果直線是標準參數方程，對涉及過定點M(x0,y0)的線段問題，優先考慮采用“參”代“普”法，直線過原(極)點，涉及到求線段長時，優先考慮用極坐標求解，對于以上兩種方法行不通的時候就可以采用“普”代“普”.在平時的學習中，應該多加歸納，靈活應用，方可優解.