初中數學“自主探究—互助互動”教學模式的實踐探究

嚴松發

平時總聽教師抱怨，某些題目已經講過n次，甚至再考原原本本題目學生還是做不了，甚至課堂上聽得懂，可題目稍變又不會做。究其原因，老師不敢讓學生自主探究、動手嘗試，甚至放棄讓學生主動探究，認為學生無法提出實質性的問題，直擊問題本質，白白浪費了教學時間，造成了學生學習數學主動性不強，容易產生信息不交流，活動不協作的情況，甚至課堂活動進行不下去，不能發揮出集體智慧的優勢，容易造成學生思維能力的局限性和狹窄性。基于以上思考，我來談談“自主探究-互助互動”教學模式在初中數學教學中的實踐探究，探索學生自主探究、互助互動學習能力培養的路徑和要領。

一、“自主探究—互助互動”的理念

自主探究是學生通過對教材課前深層次的閱讀，對知識進行一系列階梯式的追問，通過自主探究來獲得知識。學會觀察、操作及提出問題，對信息的整理和加工能促進學生自主建構知識框架，形成自己的認識。互助互動是學生通過相互幫助，相互討論的方式來交流知識，在溝通中深化自己的認識。學生在各個環節思考中一定會遇到一些問題和困惑，這就需要學生進行重新思考和互助互動，這種質疑和解疑的方式提升了邏輯推理和直觀想象能力。學生在互助互動中充分發表自己的看法，通過自我修正、彼此糾正、評講訓練等方式完成課堂探究，改變了學生的學習方式，充分合作交流，有利于學生持續性發展。

二、“自主探究—互助互動”的實施過程

具體實施步驟：自主探究，形成認識→合作學習，互助互動→展示效果，教師指導→提供練習，強化鞏固。

(一)自主探究，形成認識

學習知識的最佳途徑都是由自己去發現，教師要調動學生主動探究的積極性和主觀愿望，使全體同學真正動起來，形成自己的認識。如每位志愿者植3 棵樹，則還剩40 棵；如每位志愿者植5 棵，則還缺50棵，有多少志愿者參加植樹活動?學生在自主思考中習慣利用小學經驗列出算式(40＋50)÷(5-3)＝45，教師追問理由是什么?小組討論后部分學生無法理解。此時教師引導設志愿者有a人，學生抓住“樹木總數量”不變的前提下，學會采用3a＋40 和5a-50 兩種方式分別來表示樹木的總數量，從而完成方程的構建。列方程后，學生又會發現新問題，該如何解方程呢?接著追問如果假設這批樹的總數量，又如何找其中不變的量去構建方程呢?第二種假設思維難度明顯加大，增加了學生對“剩”“缺”的理解障礙，對用“加”還是“減”產生茫然，容易混淆。讓學生出現新的問題和困惑，體會如何對兩邊有未知數進行轉化。讓學生自己領悟到解方程時需要把未知項與常數項分開，很自然過渡到通過“還原”與“對消”的方式來解方程。在這個探究過程中有些老師急于告知答案，不敢放手讓學生嘗試，從“樹木總數量”“志愿者人數”這兩個不變的量去構建方程，使自主探究失去了原本的特性，無法做到對“剩”“缺”“多”“少”等字眼的真正理解。

(二)合作學習，互助互動

為了讓學生更熟練地掌握數學知識，通過自己的思考來解決問題，教師要引導學生面對問題時激烈討論，善于接納別人的見解，產生組內互動，甚至分工合作，在互助互動的活動中把問題解決掉，挖掘出集體思維的最大潛能。如圖1，旅游團以一樣的速度途經劉家莊、石山、綠湖、古城四地，綠湖距石山40 km，距古城80 km，問劉家莊到綠湖路程有多遠?

圖1

引導學生互助互動畫出草圖，設劉家莊到綠湖的路程為xkm，教師設計一系列階梯式的問題，讓學生探究劉家莊距石山的路程?距古城的路程?劉家莊到石山的行車時間?到古城的行車時間?根據“車速不變”列出方程。還能列出其他形式的方程嗎?借助圖形更直觀形象地理解石山到古城的路程和時間，容易發現行車的速度為60 km/h 這個不變量，列出小學算式，加深理解。還能通過不同的假設解這道題目嗎?通過不同假設，小組討論出不同的解決方案。借助圖形直觀形象地提出問題，很好串聯了小學算術與方程之間的聯系，彰顯了方程分析和解決實際問題的優點，提高了數學抽象、直觀想象能力，有利于學生思維廣闊性和深刻性的發展。

(三)展示效果，教師指導

當學生自主探究和合作學習后，形成了自己對知識的理解，教師引導學生展示學習效果，把自己對知識的理解和認識在同學面前展示出來。如①方程x2＋bx ＋c＝0 的兩根之比為1∶1，探究b與c關系?②兩根之比為1∶2 呢?③兩根之比為1∶3 呢?學生展開討論展示不同成果，有的通過兩根相等化簡后兩邊平方去掉根號；有的通過Δ＝b2- 4c＝0；個別利用因式分解(x-t)(x-t)＝0，逆推出b＝-2t，c＝t2。接著學生探究②③，顯然第一種方法運算量過大，又發現通過Δ＝0 這個方法行不通了，第三種方法具有明顯的優勢。通過學生自主探究，組內互動，學生能獨立運算出b2＝4c，2b2＝9c和3b2＝16c。學生的展示是學生對知識進行自主探究和合作思考的結果，是學生主動思考和判斷的一種最直接體現，教師要善于肯定與鼓勵。通過活動效果展示，教師及時了解到學生學習的實際情況，重新調整后續的教學設計。學生嘗到了活動帶來巨大的成就感，教師接著拋出問題，能不能進一步探究兩根之比為1∶m?兩根之比為n：m呢?學生綜合剛才運算的情境，迅速發現其中規律mb2＝(1＋m)2c和nmb2＝(n ＋m)2c。最后提出若方程改為ax2＋bx ＋c＝0(a≠0)，深化了含字母系數的一元二次方程，彰顯第三種解法的優越性，強化類比能力。

(四)提供練習，強化鞏固

教師可以給學生提供一些練習題，用實踐的方式來強化學生對知識的理解和掌握。練習會使學生對學習過的知識靈活地應用，起到練習和鞏固的目的。

如《旋轉》中①點M是等邊△ABC的BC邊上一點，把線段AM繞著點A順時針旋轉60°得到AM′，連接MM′、BM′，且MA＝MC＝2，求MM′的長。

②如圖2，點M是等邊△ABC內一點，且MA＝，MB＝1，MC＝2，求∠AMB。

③如圖3，點M是正方形ABCD內一點，且MA＝，MB＝，MC＝2，求∠AMB。

圖2

圖3

圖4

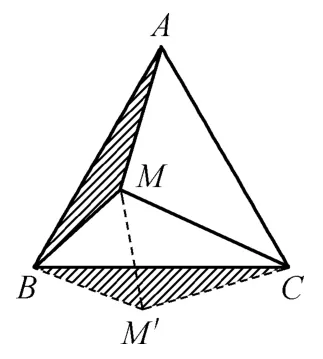
圖5

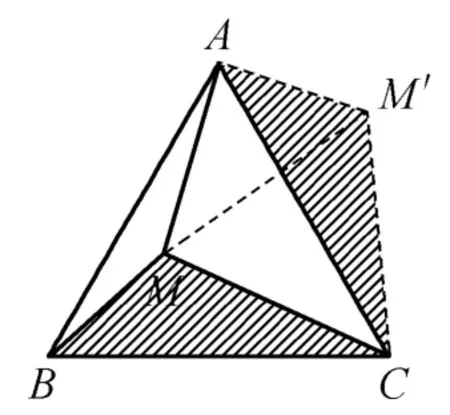
圖6

圖7

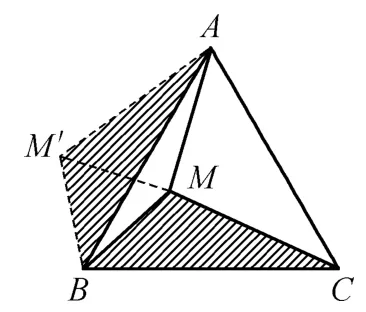
圖8

圖9

探究①學生能畫出圖形輕而易舉的解決，為后續提供解題經驗。探究②為什么要旋轉?使不在一個三角形中的邊或角能匯集到同一個三角形中，利用三角形的知識解決問題。什么情況下能考慮旋轉?圖形中具備公共端點的兩條等線段是利用旋轉法的最重要特征。那么如何旋轉呢?旋轉角是多少?通過①的鋪墊，學生容易想到本題的解題核心方法，如圖4 把△ACM繞著點A順時針旋轉，使長度相等線段AC、AB重合在一起，旋轉角度就是這兩條線段的夾角。把已知的線段通過全等三角形、旋轉等知識轉移到同一個三角形中，求出相關的角或線段。還可以怎樣旋轉呢?引導學生互助互動后，通過幾何畫板演示，讓學生發現繞著△ABC的任一個頂點都可以順時針或逆時針旋轉某一個三角形，圖4-9 展示的是“三爪六法”的解法，形成一題多解。在這個基礎上強化鞏固，把圖3 對角線AC連接起來，就演變成“三爪六法”的模型，圖形變化過程與圖形模型歸納就水到渠成了。課后與學生互動生成一系列問題：點M為一般三角形邊上一點?三角形內?三角形外?你能用同樣方法解決嗎?當學生課后回過頭看時，相較于原先思維的出發點，就做到了把思維站在高處去俯視過去。教師要重視數學思想方法的教學，要善于創造性地使用教材。引導學生從不同方位、不同角度去看待問題，循序漸進、由一般到特殊等分層次地貫徹數學思想方法，有助于提高學生數學抽象和直觀想象的思維能力，完成思維的提升。

總之，教師是課堂學習的總導演，要引導學生在數學學習中主動思考，同時還要鼓勵學生通過互助互動的方式來解決問題，自主建構全面的知識框架，大膽猜想、質疑、合作探究等分析和解決問題，有利于打造高效課堂。