基于牛頓諧波平衡法懸掛系統跌落沖擊動力學性能評價

杜興丹 陳安軍

摘要：應用牛頓諧波平衡法求解跌落沖擊條件下懸掛系統無量綱非線性動力學方程，獲得無量綱位移及加速度響應的近似解析解，并給出無量綱位移最大值、加速度最大值與跌落沖擊時間等跌落沖擊性能評價的重要參數的解析表達。同時分別與四階龍格一庫塔數值解和變分迭代解析解比較，算例分析結果表明，由牛頓諧波平衡法獲得的二、三階近似解的精度滿足工程需求，且三階近似解精度優于二階近似解。基于牛頓諧波平衡法解析解，建立系統跌落沖擊破損評價的代數方程，使系統破損邊界曲線的獲得及相關參數影響分析更加方便，為非線性系統跌落破損評價提供了一種有效的分析方法。

關鍵詞：懸掛彈簧系統;破損評價;非線性;牛頓諧波平衡法;近似解

中圖分類號：TB485.3;0328文獻標志碼：A 文章編號：1004-4523（2020）02-0331-07

DOI：10.16385/j.cnki.issn.1004-4523.2020.02.013

引言

在產品流通過程中，跌落沖擊是引起產品損傷的重要因素，跌落沖擊條件下產品動力學性能研究對產品的防護具有重要的理論意義。牛頓以產品所能承受的典型加速度脈沖幅值與速度變化量問接描述產品脆值，提出破損邊界理論，該理論適用于線性系統。實際應用中，由于緩沖材料的非線性特性，王志偉針對典型非線性系統跌落破損評價方法，建立了線性和非線性系統跌落破損評價統一理論。懸掛彈簧作為一種典型的結構非線性系統，其減振效果優于線性系統，特別適合低脆值精密儀器設備的減振防護，可使產品在不同方向獲得緩沖保護。吳曉等對懸掛系統自振及其在基礎位移激勵下的振動特性進行了深人探討;王蕾等分析了矩形脈沖激勵下懸掛系統的沖擊特性，以加速度響應峰值與脈沖激勵幅值之比為系統沖擊響應指標，脈沖激勵時問、系統懸掛角為變量構建三維沖擊譜;李輝等以考慮易損件的二自由度懸掛系統為對象，研究系統跌落沖擊條件下易損件的響應特性，并討論系統相關參數對易損件跌落沖擊特性的影響。由于非線性系統的復雜性，關于懸掛系統動力學問題的分析多采用數值分析方法，但數值方法不易獲得系統動力學響應的解析表達，系統參數對響應的影響規律難以顯函數的形式描述。宋爽等用變分迭代（VIM）法求解動力學方程，獲得懸掛系統動力學響應解析表達式，VIM法雖不依賴于小參數，但存在加速度最大值誤差較大的問題，需用能量法進行校正，其推導過程較為復雜。

牛頓諧波平衡法（NHB）將牛頓線性化方法和諧波平衡分析方法相結合，對非線性保守系統可避免單獨使用諧波平衡法時求解復雜非線性代數方程組的問題，且不依賴于小參數。該法主要用于非線性微分方程近似解析分析，更多關注系統位移響應及頻率或周期等，可獲得滿意的精度，但較少用于產品跌落沖擊動力學分析。本文將NHB法應用于懸掛系統跌落沖擊動力學分析，獲得系統位移、加速度響應最大值等重要參數的解析表達，并將結果應用于跌落沖擊動力學評價，建立系統跌落沖擊破損邊界的評價方程。

1系統動力學方程

低脆值精密儀器設備防護使用的懸掛式緩沖系統，在不考慮阻尼條件下，其力學模型如圖1所示。

3近似解精度比較

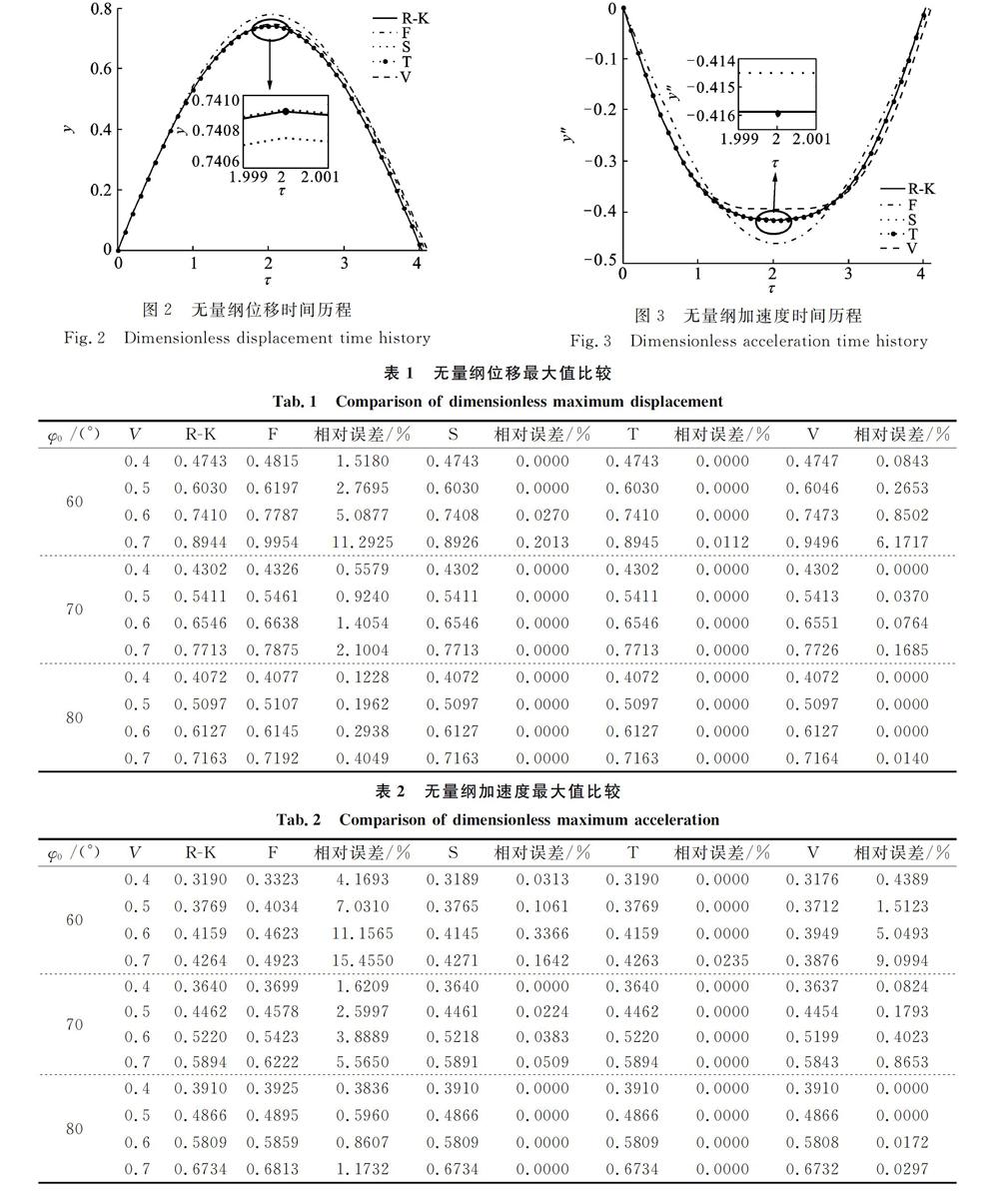
為評價NHB法近似解的精度，與四階龍格一庫塔數值解及VIM近似解比較。當無量綱跌落沖擊速度為V=0.6，系統懸掛角φo=60°時，系統無量綱位移、無量綱加速度時問歷程如圖2，3所示（R-K表示龍格一庫塔數值計算結果，F，S，T分別表示NHB一階、二階、三階近似解，V表示VIM近似解）。跌落沖擊過程系統響應位移、加速度最大值以及跌落沖擊時問是關注的重要參數。為進一步驗證解的精度，不同無量綱跌落沖擊速度及系統懸掛角，無量綱位移、加速度響應最大值以及跌落沖擊時問比較及誤差分析如表1-3所示。

由圖2及3可知，NHB法獲得的二、三階解析解（無量綱位移、加速度時問歷程）與四階龍格一庫塔數值分析結果吻合較好，三階近似解最為接近，NHB二、三階近似解優于VIM。

由表1，2及3知，相同懸掛角下，隨無量綱跌落沖擊速度增加，NHB獲得的無量綱位移、加速度最大值及跌落沖擊時問相對誤差出現增大，三階近似解相對誤差最小，表明懸掛式非線性系統近似解對初始條件敏感;相同無量綱跌落沖擊速度下，隨懸掛角減小，NHB獲得的無量綱位移、加速度最大值相對誤差增大，表明系統近似解對懸掛角同樣敏感。4跌落破損評價

5結束語

（1）應用NHB求解懸掛緩沖系統跌落沖擊無量綱非線性動力學方程，獲得系統響應一階、二階及三階解析表達式，系統響應的重要參數如位移最大值、加速度最大值以及跌落沖擊持續時問以代數方程表征，分析過程相對簡單。

（2）分別與四階龍格一庫塔數值分析及VIM近似解比較，結果表明NHB二、三階位移及加速度響應時問歷程與數值解基本吻合，無量綱位移響應最大值、加速度響應最大值以及跌落沖擊持續時問的二、三階近似結果，其精度滿足工程要求。

（3）系統的近似解對系統初始條件及懸掛角敏感。相同懸掛角下，隨無量綱跌落沖擊速度增加，系統響應無量綱位移、加速度最大值及跌落沖擊時問相對誤差增加;相同無量綱跌落沖擊速度下，隨懸掛角減小，無量綱位移、加速度最大值相對誤差增大，其原因是當系統懸掛角小于90°時，動力學方程非線性項系數小于零，垂直方向系統恢復力特性表現為三次非線性軟彈簧性能，且隨懸掛角減小，軟彈簧性能增加，非線性項的影響增加，但高階近似解可以修正非線性項的影響，使其影響減弱。

（4）NHB解析解用于跌落沖擊破損評價，獲得破損評價代數方程，有利于系統相關參數對跌落破損邊界影響分析。系統設計的重要參數懸掛角對破損邊界影響分析表明，隨懸掛角減小，對給定脆值的產品，其安全區域增大，表明通過懸掛角設計可提高系統抗沖擊能力。

懸掛式非線性系統跌落沖擊動力學響應分析表明，NHB提供了一種新的高精度解析方法，可推廣到對其他保守非線性緩沖包裝系統的動力學評價。