一種含有杠桿元件的動力吸振器參數優化

邢子康 申永軍 邢海軍 王軍

摘要：提出了一種含有杠桿元件的新型動力吸振器模型，基于H∞與H2準則進行了參數優化，并分析了減振效果。首先建立了系統的運動微分方程并求解，然后利用固定點理論和最優性能指標分別對系統參數進行H∞優化和H2優化，從而得到了兩種優化準則下的最優參數。將解析得到的結果和數值結果進行了對比，證明了求解的正確性。進一步分析了放大比對系統最優參數和主系統振幅的影響。將含有杠桿模型與經典的動力吸振器模型進行了對比，發現含有杠桿模型的減振效果優于已有的經典動力吸振器模型，可以為設計新型動力吸振器提供理論依據。

關鍵詞：振動控制;動力吸振器;參數優化;杠桿;固定點理論

中圖分類號：0328;TH113.1文獻標志碼：A 文章編號：1004-4523（2020）02-0347-09

DOI：10.16385/j.cnki.issn.1004-4523.2020.02.015

引言

動力吸振器（Dynamic Vibration Absorber，簡稱DVA）是一種附加在受激勵的主系統上以抑制其振動的控制裝置。1911年Frahm發明了第一個DVA，這種DVA只是在單自由度主系統上附加了無阻尼DVA，雖然減振效果很好但是有效頻帶很窄。1928年，Ormondroyd和Den Hartog在Frahm發明的DVA中加入阻尼，這就是目前廣為所知的Voigt式DVA。Voigt式DVA不僅減小了主系統振幅，而且拓寬了減振頻帶。加入阻尼后主系統的幅頻響應曲線上出現了兩個與阻尼無關的固定點，據此他們提出了設計DVA的固定點理論。隨后Hahnkamm與Brock根據固定點理論得到了DVA的最優頻率比與最優阻尼比。根據固定點理論設計DVA的過程稱為H∞優化，在此準則下設計DVA可以使主系統在簡諧激勵時的最大振幅最小。除H∞優化以外，還有其他優化準則，如1963年Crandall和Mark提出了H2優化準則，優化后可以使輸入主系統的功率最小;1988年Yamagu-chi提出最大穩定性優化準則，從而可以使主系統瞬態響應最快衰減。

除Voigt式DVA外，接地式DVA與三要素式DVA同樣被許多學者所研究。Ren，Liu等對接地式DVA進行了研究，利用固定點理論優化得到了接地式DVA的最優參數，與Voigt式DVA進行比較后發現接地式DVA的減振效果更好。Cheung和wong對接地式DVA進一步分析后發現Ren與Liu等得到的最優參數只是在一定質量比范圍內的局部最優參數，當系統的頻率比超過一定值時，主系統的最大振幅可以更小。Asami等對三要素式DVA進行了詳細的研究，這種DVA是將Voigt式DVA模型中的阻尼替換為黏彈性材料，經過H∞優化和H2優化后發現這種DVA在理論上可以獲得比Voigt式DVA更好的減振效果。文獻[12-15]在經典DVA中引入負剛度器件，發現負剛度器件能使主系統振幅大幅度降低，減振效果明顯優于經典DVA。文獻[16-17]研究了4種半主動DVA的近似解析解，并分析了半主動DVA的參數設計和時滯對半主動控制規律的影響。Hu等[18-19]與wang等研究了含有慣容器件的DVA，利用固定點理論與數值算法對幾種含有慣容器的DVA進行了優化，發現安裝慣容可以提升DVA的性能，但需要將慣容器安裝在合適的位置。

杠桿作為一種具有力放大功能的簡單機械元件，用于振動系統中可以抑制振動的幅度。1967年Flannelly在隔振器中引入杠桿元件，設計出了一種新型隔振器——動力反共振隔振器（DynamicAnti-resonant Vibration Isolator，簡稱DAVI）。這種隔振器利用杠桿的特點，放大了質量產生的慣性力來抵消彈簧力從而產生反共振，在獲得同樣隔振效果時質量更小。文獻[22-23]中基于DAVI設計了轉子隔振系統，并已應用在直升機上。文獻[24-25]中將兩級和多級杠桿引入隔振器，使隔振器在低頻時有效帶寬增加。文獻[26]中將x型剪式叉架作為杠桿式隔振器的支撐，使隔振器擁有更好的隔振性能。文獻[27]中將杠桿元件引入隔振器，提出了三種新型隔振器，發現使用杠桿元件不僅能提高隔振性能，而且在設計上約束更少。文獻[28]提出一種新型杠桿調諧質量阻尼器，減小了調諧質量阻尼器安裝空問。文獻[29]提出了一種含有杠桿的新型橋梁減振裝置，不僅獲得了良好的減振效果，而且便于安裝維護。文獻[30]提出一種杠桿式非線性能量阱，與傳統非線性能量阱相比能在較小附著質量時獲得優異的減振性能。

本文通過在經典Voigt式DVA的基礎上引入杠桿，對其進行H∞與H2優化并分析減振性能。通過與其他經典被動式DVA模型的對比表明，本文所提出的DVA模型在減振方面具有很大優勢，能夠有效降低共振幅值，減少系統輸人能量，同時拓寬了減振頻帶，為設計新型的DVA提供了一種選擇。

1動力吸振器模型建立及求解

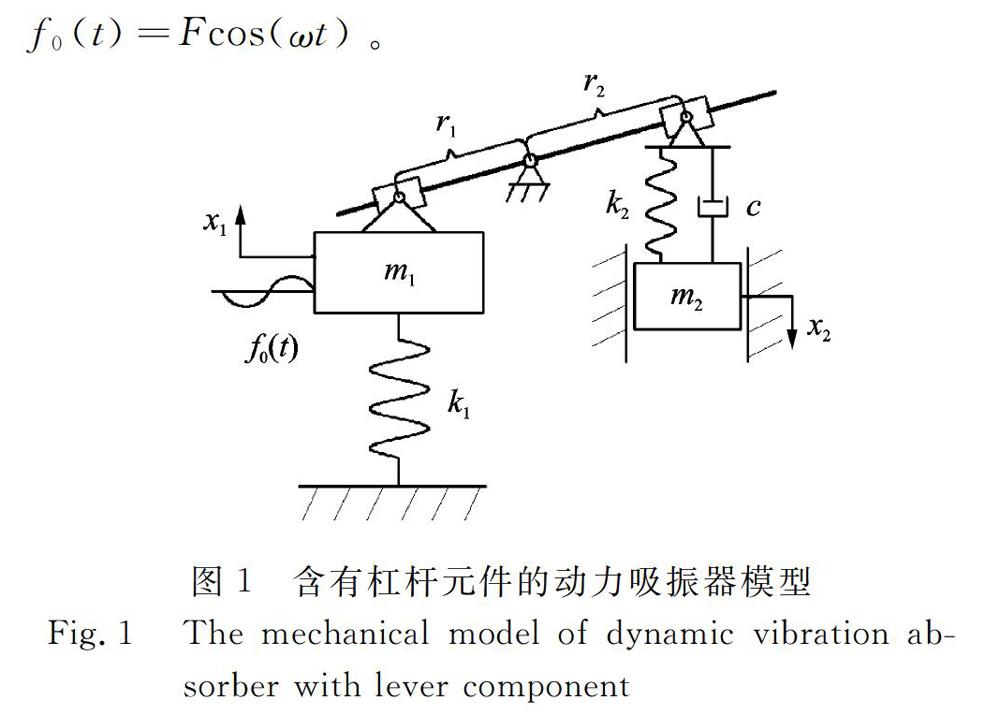
圖1所示為本文所提出的含有杠桿的DVA模型，該模型是在Voigt式DVA的基礎上增加一個固定在支點位置的杠桿，通過滑塊將杠桿與主系統、DVA連接到一起。圖1中杠桿的阻力臂與動力臂分別為r1與r2主系統質量為m1，彈簧剛度為k1;DVA質量為m2，彈簧剛度與阻尼系數分別為k2與c;主系統與DVA的位移分別為x1與x2激振力fo（t）=Fcos（cot）。

根據相似三角形定理可知，系統在振動時r2與r1的比值恒定，定義杠桿的放大比為L=r2/r1，阻力臂受到的力為動力臂的L倍，動力臂處的位移為阻力臂處的L倍。忽略杠桿質量與系統中的摩擦，假設系統為微小振動，忽略非線性因素，由牛頓第二定律可得到該系統的運動微分方程為

2動力吸振器參數優化

下面針對圖1所示DVA在不同的減振要求下進行參數優化。

2.1H∞優化

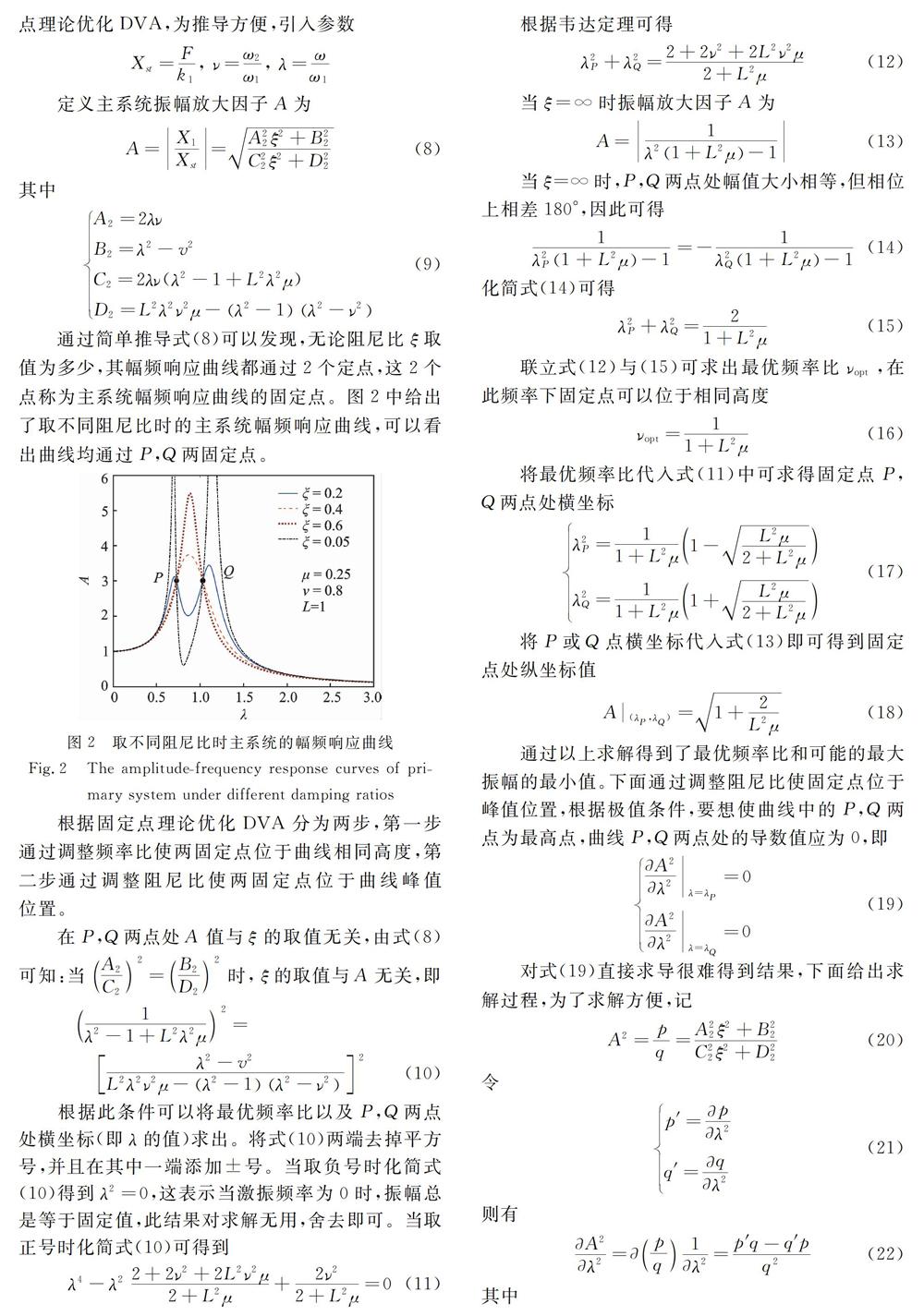
H∞優化是指主系統受到外界簡諧激勵時，在安裝DVA后主系統最大振幅最小。下面使用固定點理論優化DVA，為推導方便，引人參數

至此已經將H∞優化中的最優參數vopt和εopt求出。按照固定點理論進行優化的最優參數只是近似最優解，但在常用質量比u<0.2的范圍內與精確解析解相差很小，可以滿足工程實際需要。

2.2H2優化

H2優化是指主系統受隨機激勵情況下，在安裝DVA后主系統整個幅頻響應曲線下的面積最小，即輸入主系統的功率最小。假設主系統所受的激勵為理想的白噪聲，在H2優化中，優化的性能指標由下式定義，通過使性能指標最小化來求得最優參數

3.3放大比L與主系統振幅的關系

放大比L的取值與主系統最大振幅有很大的關系，這里給出了L取不同值時主系統的幅頻響應曲線，發現當L取值足夠大時H∞優化中最大振幅趨向于1，而H2優化中最優性能指標接近于0。圖9與10為系統參數u=0.1，L取不同值時主系統的幅頻響應曲線圖。在圖9中可以看到L=1000時系統最大振幅趨近于1，圖10中L=1000時曲線下的面積趨近于0。

4與經典動力吸振器模型對比

4.1主系統幅頻響應曲線對比

為證明本文模型減振效果，分別在H∞優化和H2優化下與Voigt式、接地式及三要素DVA進行比較。除接地式動力吸振器H2優化的最優參數以外，文獻[7，11，13，32]已給出了三種經典DVA的最優參數求解公式及振幅放大因子A的形式。通過優化可得到接地式DVA的H2優化最優參數為

選取系統參數u=0.1，L=3，繪制各類型DVA主系統幅頻響應曲線，可得到圖11與12中的結果。由圖11可以看到本文模型能夠大幅度降低共振峰區域振幅，圖12中幅頻響應曲線下的面積有效減小，減少了輸入主系統的功率，證明減振效果良好。

4.2在隨機激勵下主系統位移的時間歷程對比

因為在工程中系統所受激勵大多為隨機激勵，這里給出幾種安裝不同DVA的主系統在受到隨機激勵時的系統響應，并且將本文的H2優化結果與幾種DVA模型進行對比。

假設主系統受到均值為0、功率譜密度為s（ω）=So的白噪聲激勵，則它們的絕對位移響應的功率譜密度函數分別為

從式（40）可以發現，本文模型的主系統位移響應均方值最小，說明本文模型擁有良好的減振效果。

為了更加直觀地揭示本文模型的減振效果，構建50s均值為0、方差為1的隨機力激勵，其時問歷程如圖13所示。選取系統參數：主系統質量m1=1kg，主系統剛度k1=100N/m，吸振器質量m1=0.1kg，其余最優參數根據文獻[11，32]可得。將隨機力激勵分別作用于無DVA模型、本文模型、Voigt式模型、接地式模型與三要素模型，其中無DVA模型為單自由度無阻尼系統。可以得到在同樣的系統參數下，無DVA以及采用不同DVA模型時主系統位移的時問歷程圖，分別如圖14-18所示。

主系統的位移方差往往與系統振動能量的波動相關，表1總結了主系統位移方差及其衰減比。從圖14-18及表1可以看到DVA在振動系統中的作用，以及含杠桿式吸振器的減振優勢。

5結論

提出了一種含有杠桿元件的DVA模型，對其進行了H∞與H2優化，利用固定點理論與最優性能指標分別求出了H∞與H2優化中的最優參數。在求得最優參數后，對其進行數值仿真，證明了求解過程和結果的正確性，同時給出了放大比與系統最優參數及主系統振幅的關系。將本文模型與傳統的DVA模型進行多方面的對比，發現本文模型能夠大幅度降低主系統的振幅，并且拓寬了減振頻帶，減少了輸入主系統的功率，證明了含杠桿式DVA的減振效果。通過對比說明了本文模型具有較大優勢，為以后設計新型DVA模型提供了參考依據。