以點帶面，糾錯解惑，水到渠成
——一節初中數學復習課的設計與思考

江蘇省南京市將軍山中學 曹小龍

2019 年5 月，我執教了一節市級研究課——蘇科版數學七年級下冊第11 章《一元一次不等式》復習課，受到好評。現嘗試對教學過程進行簡述和評析，旨在探索初中數學章節復習課的設計與思考。

一、設計實錄

活動一：知識梳理

師：同學們，今天我們一起來復習《一元一次不等式》（板書課題），首先請完成下列小題。

1.基礎訓練

（1）某種小客車載有乘客x 人，那么載客超過20 人可用不等式表示為__________。

（2）若a ＞b，則下列各式中一定成立的是__________。（填序號）

①a+2 ＞b+2； ②-2a ＞-2b；③ac ＜bc；④3-a ＜3-b。

（3）不等式2-x ＞0 解集是____。

師：（約3 分鐘）請同學展示，并思考每一小題能告訴我們些什么？

生1-生4 上臺展示并解析，教師順勢提煉并板書：實際問題（不等關系）→不等式（概念）→性質→解法（解集）→一元一次不等式（組）→實際問題（模型）。

2.知識框架

師：接下來同學們能自己嘗試建構出本章的知識網絡圖嗎？

生：……（約3 分鐘，教師巡視并選擇2 位建構各有特色的學生展示講評）

設計意圖：本環節是課堂結構中的知識梳理環節，旨在通過基礎訓練回顧所學知識，構建知識框架，預設時間約10 分鐘。由知識點編寫題目，學生解決問題，教師以問題為載體引導學生回顧所學知識，在此基礎上，構建知識框架。

活動二：解惑糾錯

師：老師是個有心人，在批改同學們作業的時候收集了一些“作品”，請大家評析（見圖1）。

……

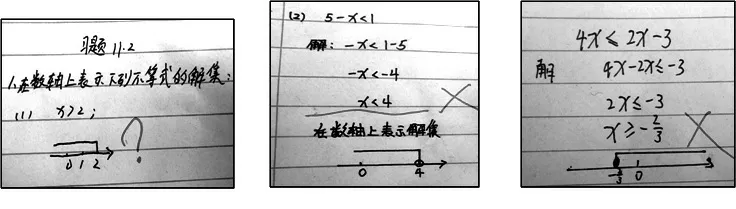
圖1

生：……（獨立思考約3 分鐘后，逐題點評并矯正展示，教師順勢板書易錯點）

師：同學們有了剛剛糾錯的經驗，請小結解不等式（組）的易錯點。

生1-生3：（1）符號方向問題：不變號，亂變號；（2）數軸及方向問題：畫反，不畫；（3）空實心問題；（4）去括號問題：不變號，漏乘；（5）去分母問題……

師：補充得非常好！有解方程時會犯的錯誤，也有新的問題出現。請大家快速整理寫在學習單上。

設計意圖：本環節在課堂結構中是解惑糾錯環節，通過錯題資源呈現，交流、評價、反思與總結。預設時間約7 分鐘，要求收集學生平時作業中（或教師編寫）一些模糊不清的概念和典型錯誤幫助學生查漏補缺并優化解題方法。

活動三：鞏固提高

師：了解了易錯點，下面請完成一道例題。

師：請你來點評。（教師展示經巡視發現的有典型錯漏的學生解答兩例）

生：……（師追問：有什么新的問題出現了嗎？生：格式規范，審題不全，漏寫特殊解。教師板書并展示規范正確的學生解答）

師：我們知道和方程一樣，不等式也是刻畫現實世界的數學模型之一，下面來看一道實際問題。

例2：小明準備用21 元買筆和筆記本。已知筆每枝3 元，筆記本每本4 元，如果小明買了1 本筆記本，那么他最多還可以買幾枝筆？

師：請你來點評。（教師展示典型錯漏的學生解答兩例）

生：……（師：我們應該如何來解這類實際問題？追問：為什么“設”中不能有“最多”二字？生：21 元不一定能正好用完，問題是要我們找解集中的特殊解而已……）

根據當時反饋的較好學情，教師適時拋出這樣一個問題：

師：你能給出不等式3x+4≤21 不同的實際意義，編制一道類似的問題嗎？先獨立思考再小組交流（教師參與，氣氛熱烈），代表發言。

生1：……（簡單把筆和筆記本換成其他物品，教師肯定并建議同學們變一變）

生2：某小區有一免費停車場，停著三輪車若干輛和小汽車1 輛，小明同學數車輪玩，發現不超過21 個車輪，那么最多幾輛三輪車？

生3：某中學七年級有21 人被推薦參加數學競賽，被安排在某校宿舍住宿，他們都想住一樓，若每間住3人，至少還剩4 人住不下。那么一樓最多有幾間房？……

師：他們編得對不對，你有沒有不同意見？（師生達成共識）

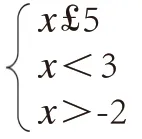
很快有學生畫數軸完成解答，教師展示并追問，使學生進一步體會化歸、轉化及數形結合的思想。

設計意圖：本環節通過選取具有代表性的例題，解析、展示、交流與反饋，預設約20 分鐘。例題要有具體綜合性，知識點要盡量覆蓋復習的內容，并注意整合；解題時要體現“通性通法”，重視一題多解，一題多變。解答后，要引導學生反思解題過程，總結方法與經驗，配備適當的拓展練習予以強化并注意解題規范性指導。

活動四：反思總結

師：請同學們談談本節復習課的收獲、困惑與感想。

生：……（在知識方面、思想、方法等方面，教師加以引導補充）附結構圖（見圖2）：

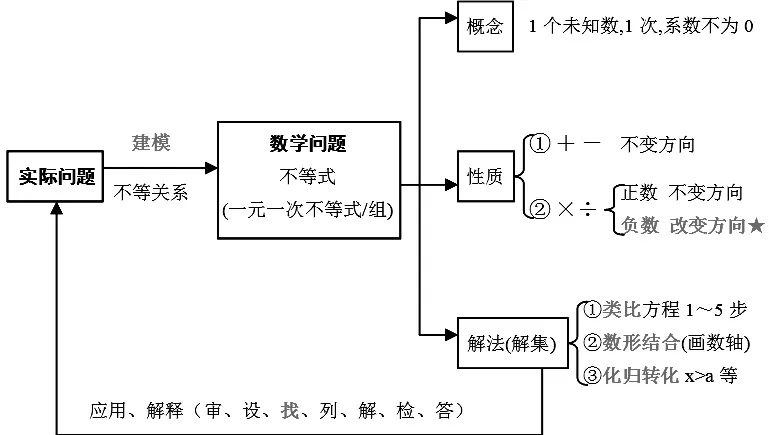
圖2

設計意圖：本環節旨在引導學生總結經驗、彌補不足，時間約3 分鐘，要求完整地歸納概括復習內容，總結基本題型及解法，概括總結數學思想方法，進一步強調復習過程中暴露出的問題。

活動五：達標檢測

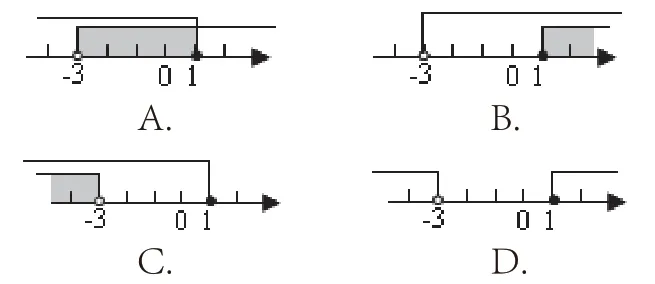
3.某次知識競賽有50 道選擇題，評分標準：答對1 題得2 分，答錯1題扣1 分，不答不得分也不扣分。某學生4 道題沒答，但得分超過70 分，那么他至少答對了多少道題？

設計意圖：達標檢測環節旨在抓住基礎知識、基本技能和基本方法，突出重點內容的達標反饋，約5 分鐘，要求控制練習題目的難度，有效覆蓋知識點，形式多樣，避免大量重復的機械練習；要突出重點，關注學生易錯點；重視對練習的評價、反饋，對其中暴露的缺陷和不足應及時矯正、補償。

二、案例反思

1.以點帶面，建構知識框架

對于概念較多的復習課，適宜以練習提煉知識點，逐步構建知識結構。本節課中在設計選題時，每一小題對應一個大知識點，以題理知，教師適時板書要點，為下面學生自主建構、豐富知識框架作好鋪墊，自然節省時間，有效引導學生從整體理解知識之間的聯系和區別。

2.糾錯解惑，作好查漏補缺

“錯誤是正確的先導，是通向成功的階梯。”如果教師能科學糾錯，就能提高學生分析、解決問題的能力，培養思維的批判性。本課向學生展示平時作業，親切生動，激起關注熱情。讓他們經歷評價、矯正的過程，提高糾錯的效率，從而達到反思完善的目的。

3.用知得法，適當延伸拓展

課堂中出現的每一道例題，都必須為本課的教學目標服務。本課教師精心選題，把發現錯誤的機會留給學生，并站在更高的角度去指導學生，引領學生走出認知誤區。另外根據學情，靈活調整，促進精彩生成。比如講解例2 之后，根據例2 所得一元一次不等式，讓學生賦予不同的實際意義并編制問題，從本課生成效果來看，實為亮點。

4.反思總結，分享全課收獲

讓知識從感性上升到理性，讓方法從模糊走向清晰，讓思想滲透從有形變為無形，這就是小結提煉的最主要的作用。給足時間和空間，讓學生回顧本課數學知識、解題方法、數學思想等，對學生接下來的檢測有極大的指導作用。

5.限時檢測，拉動學生提升

當堂檢測可有效診斷課堂有效性。題目編排須緊緊圍繞教學目標，在學生完成規范解答后，教師巡批、交換批閱和一兩分鐘的自主訂正，給學生的反思“悔過”留下了時間和空間。“選做題”的設置，在讓全體同學學有所獲的同時，為學有余力的學生留下了自我拓展的空間。

復習課要以點及面、由知及能、由能及智。本課知識立意，兼顧能力培養，重經驗積累和思想滲透，強化雙基的同時關注分層。通過以點帶面，糾錯解惑等環節，以學定教，順學而教，直至水到渠成！