離散元仿真中挖掘機鏟斗結構表面的單元球表示方法探究

方自強

離散元仿真中挖掘機鏟斗結構表面的單元球表示方法探究

方自強

（江漢大學 機電與建筑工程學院，湖北 武漢 430056）

提出了一種基于單元球的鏟斗結構表面的多精度幾何表示方法。該方法針對鏟斗的斗底板、側腹板、側刀板、前刀板和斗齒5個部位的幾何特征和功能要求，實施基于單元球的多精度幾何表示。對比分析不同精度下單元球表達的鏟斗結構表面，發現離散元仿真時間會隨鏟斗結構表面的幾何表示精度的提高而增加。因而，鏟斗結構表面的單元球表示需綜合考慮仿真精準性與仿真時間的需求。對比分析不同精度下單元球與三角面片表示方法，證實了單元球表示方法具備有效表示鏟斗結構表面的局部幾何細節的能力。相比于三角面片表示方法，單元球表示方法有望在鏟斗挖掘過程離散元仿真中花費更少的計算時間。

挖掘機鏟斗；結構表面；幾何表示；離散元仿真；單元球

顆粒離散元法[1]主要用于模擬工業過程中顆粒與結構表面間的碰撞行為，如挖掘機鏟斗對顆粒散料的挖掘過程[2-3]。通過在一個足夠小的時步內更新顆粒的位移、速度、加速度和接觸力等參數[4]，離散元法可以獲取顆粒與鏟斗表面間相互碰撞過程中的接觸速度、碰撞能量等信息[5]。

挖掘機鏟斗的結構表面表示是離散元仿真的一項關鍵技術[6]，它直接影響著散料挖掘過程離散元仿真的接觸檢測效率以及接觸力求解的精準性。目前，三角面片是離散元仿真中使用最為廣泛的一類結構表面表示方法[7]。利用ICEM CFD等網格劃分工具對鏟斗結構表面進行三角面片劃分，這些三角面片可有效描述鏟斗結構表面的幾何形狀。經三角面片表示，顆粒與鏟斗表面間的接觸檢測可以轉化為顆粒與三角面片間的接觸檢測。于是，在一個顆粒與一個三角面片間的相交求解中，該顆粒需要與此三角面片的面、邊和點相繼進行相交求解，從而導致了巨大的仿真計算開銷。

由于單元球與單元球間的接觸檢測僅涉及一個中心距和兩個半徑和之間的比較[6]，因而單元球與單元球間的接觸檢測效率有望遠高于單元球與三角面片之間的接觸檢測效率。因此，本文以離散元仿真中常見的挖掘機鏟斗結構表面為對象[8-9]，開展不同分辨率下的單元球表示方法的探究。

1 基于單元球的鏟斗結構表面的多精度幾何表示方法

1.1 鏟斗結構表面幾何表示精度的解析

在鏟斗結構表面的幾何表示之前，首先需要根據離散元仿真對鏟斗結構表面的幾何特征和功能要求[10]，進行幾何表示精度的解析。如圖1所示，挖掘機鏟斗由斗底板、側腹板、側刀板、前刀板和斗齒共5個部件組成[11-12]。鏟斗的挖掘作業包括挖掘、回轉、卸料和返回四個過程。在挖掘與回轉過程中，斗齒[13]對顆粒堆表面進行剝離作業，因而承受了顆粒的絕大部分接觸力，而側刀板和前刀板也與顆粒發生直接碰撞。相對而言，斗底板和側腹板主要用于顆粒散料的裝載[14-15]，因而較少受到顆粒的沖擊和磨擦。

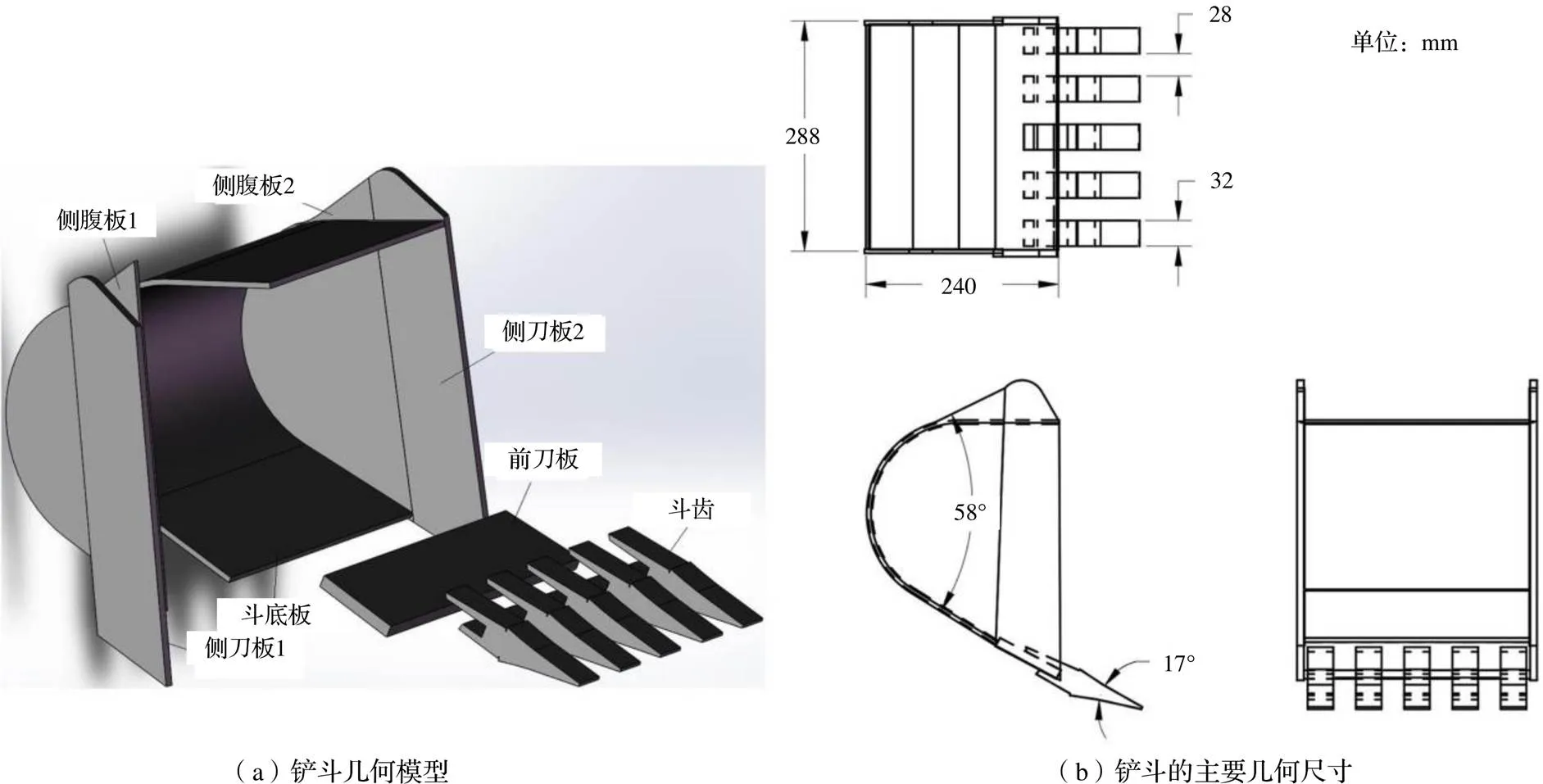
圖1 鏟斗的幾何模型與尺寸

為了利用離散元仿真有效分析挖掘機作業中顆粒對鏟斗結構表面的沖擊和磨擦[16-17]，需要對鏟斗結構表面的不同部位進行不同精度的單元球幾何表示。例如，斗齒表面與顆粒的接觸最為頻繁，該部位需要進行高精度的幾何表示；側刀板和前刀板也要長時間承受顆粒的作用力，它們的幾何表示精度要求也相對較高；斗底板和側腹板較少受到顆粒的沖擊和磨擦，對這兩個部位進行低精度的幾何表示。于是，在本文的鏟斗結構表面的幾何表示中，斗底板和側腹板的表示精度最低，側刀板和前刀板的表示精度是它們的兩倍，斗齒的表示精度是它們的三倍。

在采用單元球對鏟斗結構表面進行幾何表示的過程中，決定鏟斗結構表面幾何表示精度的參數主要包括相鄰單元球之間的中心距離和單元球的直徑d。因而在相鄰單元球之間的保持一定的前提下，有：

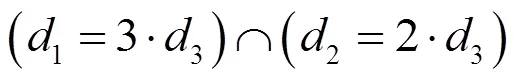
式中：1為斗底板和側腹板的單元球直徑，mm；2為斗底板和側腹板的單元球直徑，mm；1為斗齒的單元球直徑，mm。

此外，在d保持一定的前提下，有：

式中：1為斗底板和側腹板的相鄰單元球之間的中心距，mm；2為側刀板和前刀板的相鄰單元球之間的中心距，mm；3為斗齒的相鄰單元球之間的中心距，mm。

1.2 鏟斗結構表面的單元球多精度幾何表示

根據上述解析，依據式（1）所給出的通過變化d來改變鏟斗結構表面的不同部位幾何表示精度的方式，分別對圖1（a）中的斗底板、側腹板、側刀板、前刀板和斗齒五個部位進行幾何重構和三角面片劃分[18]。

首先，利用三維CAD軟件，對上述結構表面進行表面內偏移操作，完成幾何重構。當表示斗底板和側腹板、側刀板和前刀板、斗齒結構表面的單元球直徑分別被設置為15 mm、10 mm、5 mm時，它們各自對應的內偏移距離分別為7.5 mm、5 mm、2.5 mm。如圖2（a）和（b）所示，重構后的斗底板和側腹板分別由曲面和平面來表示。如圖2（c）、（d）和（e）所示，重構后的側刀板、前刀板和斗齒幾何形狀則由相應幾何體的外殼表面來表示。

然后，利用ICEM CFD或Gambit等軟件，對幾何重構后的結構表面進行三角面片劃分。在結構表面的三角面片劃分中，三角面片的最大尺寸依據各自單元球的直徑來確定。在結構表面的單元球幾何表示中，要求單元球之間不存在縫隙，能夠相互重疊，于是三角面片劃分的最大尺寸需要設定得小于或等于單元球的直徑。如圖2（a-1）、（b-1）、（c-1）、（d-1）、（e-1）所示，重構后的斗底板和側腹板、側刀板和前刀板、斗齒的結構表面被分別劃分為最大尺寸為12 mm、8 mm、4 mm的三角面片。

最后，以各個三角面片的頂點為依據，在斗底板和側腹板、側刀板和前刀板、斗齒對應的三角面片頂點上分別添加直徑為15 mm、10 mm、5 mm的單元球，可實現如圖3（a）所示的鏟斗結構表面單元球多精度幾何表示[6]。

需要說明的是，依據式（2）所給出的通過變化相鄰單元球之間的來改變鏟斗結構表面的不同部位幾何表示精度的方式，同樣可以實現鏟斗結構表面的單元球多精度幾何表示。其中，相鄰單元球之間的對應于幾何重構后結構表面三角面片劃分中三角面片的尺寸大小。

2 鏟斗結構表面單元球表示方法的性能分析

2.1 三種不同的最大中心距下單元球表示方法的性能分析

通過上述基于單元球的鏟斗結構表面多精度幾何表示方法，本文在采用相同單元球粒徑d的前提下，通過變換單元球間的中心距離，開展三種不同最大中心距max下單元球表示方法的性能分析。

依據式（1），用于表示斗底板和側腹板、側刀板和前刀板、斗齒結構表面的d分別為15 mm、10 mm、5 mm。在三種單元球表示精度中，單元球間的max分別為0.8d、0.6d和0.4d，具體相關尺寸由表1列出。

圖2 鏟斗模型的幾何重構與三角面片劃分

表1 三種不同表示精度下單元球間的最大中心距zimax

圖3分別給出了max為0.8d、0.6d和0.4d的條件下，采用多粒徑單元球表示的鏟斗結構表面的幾何形狀。隨著max的逐漸減小，鏟斗結構表面的幾何表面更加平滑。這說明鏟斗結構表面的幾何表示精度隨著max的減小而增加，更有益于鏟斗對顆粒挖掘過程離散元仿真精度的提升。

此外，上述三種max所表示的鏟斗結構表面的單元球數量分別為91342、161317、354328。在離散元仿真中，顆粒與結構表面間接觸檢測的鄰居檢索時間復雜度[18]可表示為：

式中：N為顆粒的總數量；N為單元球的總數量；為一個與顆粒尺寸和分布相關的經驗參數；{1,2}?[1, 2]。

于是，隨著單元球數量的增加，顆粒與結構表面間接觸檢測的時間消耗會呈幾何級數的增長，不利于離散元仿真效率的提高。因此，在進行鏟斗結構表面的單元球表示時，需綜合考慮仿真時間與仿真精準性的需求，以確定單元球間的max。

2.2 三種不同的單元球直徑下單元球表示方法的性能分析

類似地，在保持單元球間max一致的前提下，通過改變d，開展三種不同d下單元球表示方法的性能分析。依據式（1），用于表示鏟斗結構表面的單元球之間的max均為0.8d，三組用于表示鏟斗結構表面的單元球直徑1、2和3分為等于D、0.8D和0.6D，其中D為圖2中鏟斗結構邊界的內偏移距離。于是，得出d和max值如表2所示。

在單元球直徑d為D、0.8D和0.6D條件下，采用多粒徑單元球表示的鏟斗結構表面的幾何形狀分別如圖4所示。當單元球之間的max為0.8d時，鏟斗結構表面的幾何表示精度隨著d的減小而顯著提高。因此， d的減小有益于鏟斗結構表面的幾何表示精度的提升。

如圖4所示，用于表示鏟斗結構表面的單元球數量分別為91342、148957、279848。根據式（3）給出的顆粒與結構表面間接觸檢測的時間復雜度，離散元仿真中顆粒與結構表面間接觸檢測的時間消耗會隨d的降低而顯著增大。因此，在鏟斗結構表面的單元球表示中，d的選擇也是決定離散元仿真效率與鏟斗結構表面幾何表示精度的重要參數之一。

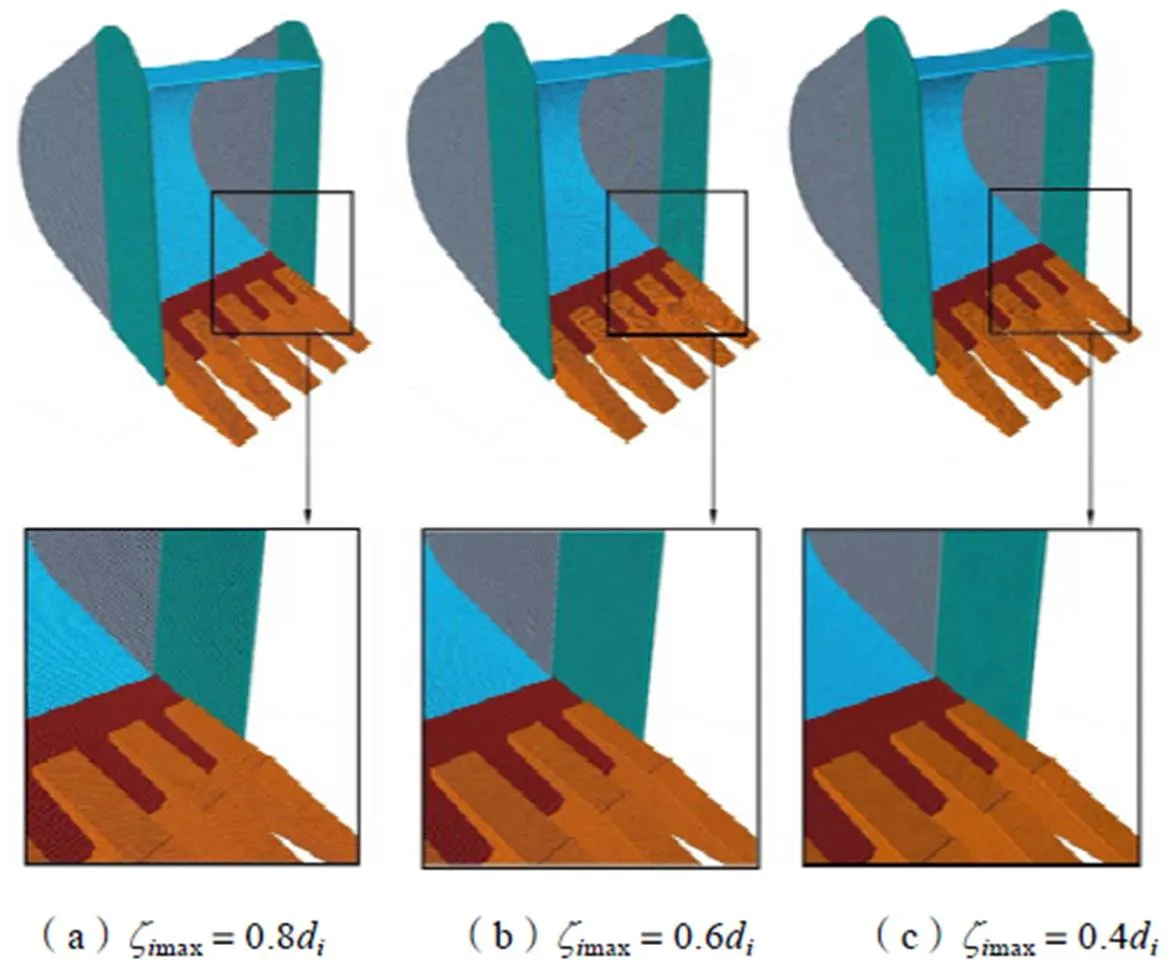
圖3 三種不同最大中心距下單元球表示的鏟斗結構表面

表2 三種不同表示精度下單元球的粒徑di和最大中心距zimax

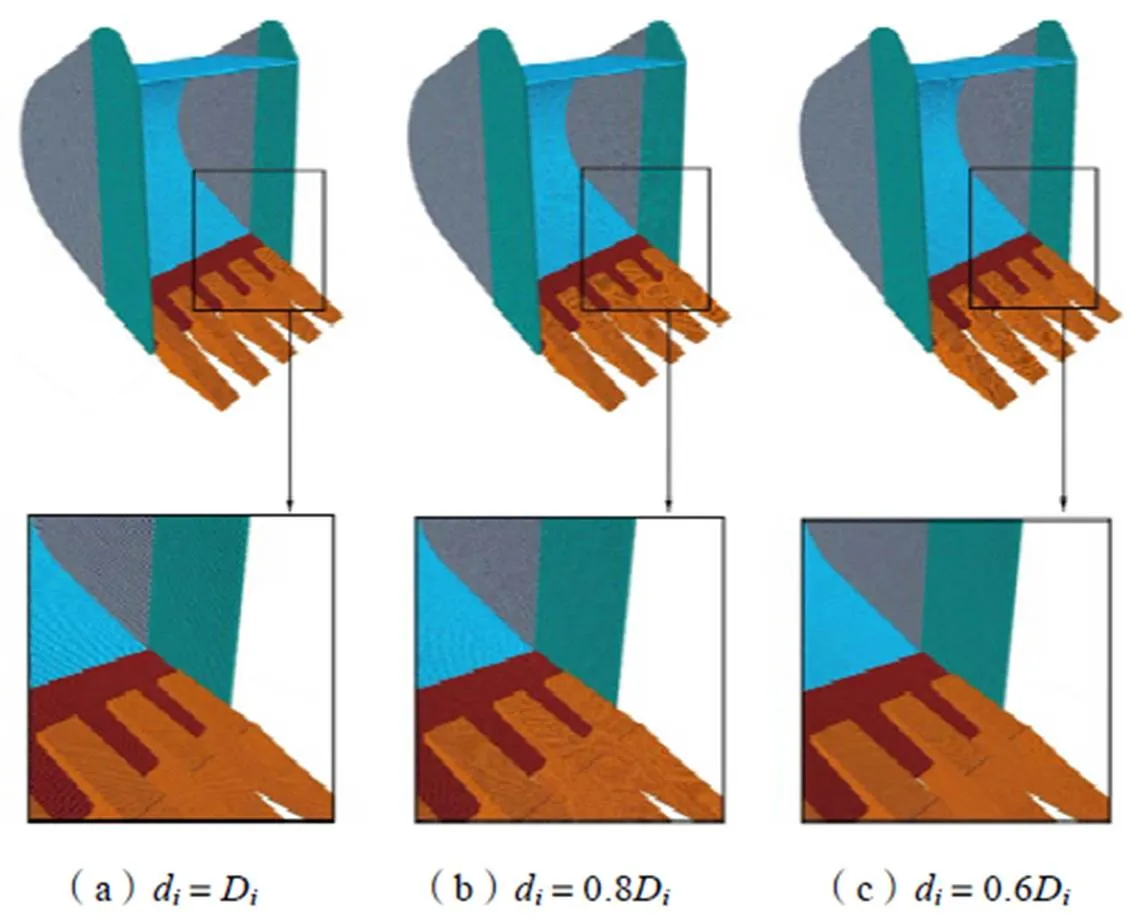
圖4 三種不同di下單元球表示的鏟斗結構表面

3 單元球與三角面片表示方法的性能比較及分析

3.1 幾何表示精度的比較

為了對比分析單元球與三角面片[7]表示方法的性能，本文以圖1所示的鏟斗各部位的殼體表面為對象，利用ICEM CFD工具，分別對斗底板和側腹板、側刀板和前刀板、斗齒進行三角面片劃分，其中三角面片尺寸以表1所列出的max為依據。于是，對應于圖3中由單元球表示的鏟斗結構表面，圖5給出了由三角面片表示的鏟斗結構表面。

在圖5中，三角面片的數量分別為227844、403008和909658。隨著三角面片尺寸的減小，三角面片所表示的鏟斗結構表面的幾何精度顯著提升，這與單元球表示的鏟斗結構表面的幾何精度隨著的變化規律一致。

此外，通過對比同一精度下由單元球和由三角面片表示的鏟斗結構表面的幾何形狀，可發現單元球能夠有效表示鏟斗結構表面的局部結構細節，因而能夠有效表示上述不同精度下鏟斗結構表面的幾何形狀。

圖5 三種不同精度下三角面片表示的鏟斗結構表面

3.2 接觸檢測時間消耗的理論分析

根據式（3）所給出的時間復雜度，在顆粒數量相同的前提下，單元球與三角面片表示方法對應的顆粒與結構表面間接觸檢測的鄰居檢索的時間復雜度在同一個數量級。

對于相交求解，一個單元球與一個球形顆粒間的相交求解條件為：

參照文獻[7,18]，一個三角面片與一個球形顆粒間的相交求解涉及三角面片的一個面、三條邊和三個角與球形顆粒間的連續求解操作。于是，本文將一個單元球與一個球形顆粒間的相交求解以及一個三角面片與一個球形顆粒間的相交求解[7]的計算操作符號數量進行對比，如表3所示。

在以C++為語言的離散元仿真的算術運算中，“+”、“-”、“′”、“/”等計算操作符號為基本符號，其計算時間消耗較小，而“||-||”、“|-|”、“?”、“acos(-)”、“min(-)”等計算操作符號是以“+”、“-”、“′”、“/”為基礎的復合計算操作符號[19]，所消耗的計算時間十分巨大。

如表3所示，一個單元球與一個球形顆粒間的相交求解僅涉及一個“+”、一個“||-||”和一個“>”。相較而言，一個三角面片與一個球形顆粒間的相交求解所涉及的“+”、“-”、“′”、“/”等計算操作符號是一個單元球與一個球形顆粒間的相交求解對應操作符號數量的若干倍，并且還涉及多個“||-||”、“|-|”、“?”、“acos(-)”、“min(-)”等復合計算操作符號。因而，單元球與顆粒間的相交求解時間消耗遠小于三角面片[7,18]與顆粒間的相交求解時間消耗。可以期望的是，采用單元球表示鏟斗結構表面的幾何形狀會在離散元仿真中花費更少的計算時間，更有利于離散元仿真計算效率的提高。

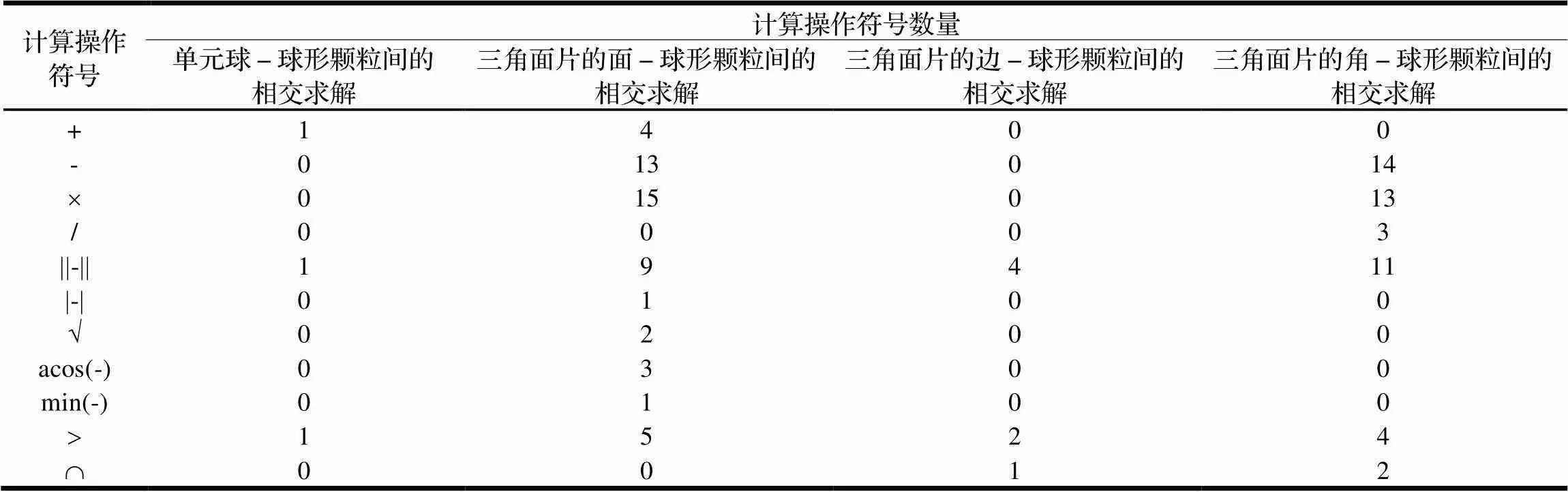
表3 相交求解的計算操作符號數量

4 結論

（1）本文提出了一種基于單元球的鏟斗結構表面的多精度幾何表示方法，該方法針對鏟斗不同部位的幾何特征和功能要求，實施不同的單元球粒徑和不同最大中心距的多精度幾何表示。

（2）對比分析三種不同精度下單元球表達的鏟斗結構表面，發現鏟斗結構表面的幾何表示精度以及顆粒與結構表面間接觸檢測的時間消耗均隨著的減小而增加。因而，鏟斗結構表面的單元球表示需綜合考慮仿真精準性與仿真時間的需求，以確定單元球間的max。

（3）對比分析三種不同精度下單元球與三角面片表示方法，可知單元球具備有效表示鏟斗結構表面的局部幾何細節的能力。相比于三角面片方法，單元球表示方法有望在離散元仿真中花費更少的計算時間，更有利于仿真效率的提高。

[1]方自強，吳洪亮，周享楠. 球磨機DEM 仿真中接觸模型的精準性分析[J]. 機械，2019，46（2）：17-24.

[2]C. J. Coetzee，A. H. Basson，P. A. Vermeer. Discrete and continuum modelling of excavator bucket filling [J]. J. Terramechanics，2007（44）：177-186.

[3]滕忠斌. 雙斗輪取料機改造分析[J]. 機械，2016，43（11）：23-29.

[4]胡國明. 顆粒系統的離散元素法分析仿真[M]. 武漢：武漢理工大學出版社，2010.

[5]J. Maciejewski，A. Jarzebowski. Laboratory optimization of the soildigging process [J]. J. Terramechanics，2002（39）：161-179.

[6]胡勵. 機械產品設計中的顆粒離散元仿真技術及實現[D]. 武漢：武漢大學，2013.

[7]M. Kremmer，J. F. Favier. A method for representing boundaries in discrete element modeling-part I: geometry andcontact detection [J]. Int. J. Numer. Meth. Eng.，2001（51）：1407-1421.

[8]P. W. Cleary. DEM prediction of industrial and geophysical particle flows [J]. Particuology，2010（8）：106-118.

[9]侯亞娟，王吉生，李愛峰，等. 離散元法及其在鏟斗設計中的應用[J]. 工程機械，2014（45）：23-29.

[10]涂宇，王怡，劉愛云，等. 挖掘機工作裝置機械-液壓聯合仿真系統的建立與優化[J]. 內燃機與配件，2019（23）：63-65.

[11]馮豪，杜群貴，于樹棟. 液壓挖掘機挖掘動力學建模研究[J].振動與沖擊，2019（13）：242-248.

[12]閻書文. 機械式挖掘機設計[M]. 北京：機械工業出版社，1982：12-75.

[13]靳海軍. 大型挖掘機斗齒定位監測系統研究[J]. 工程機械，2019（11）：95-98.

[14]M. B. Sr?an，A. A. Miodrag，B. G. Neboj?a，L. J. M. Ivan，M. A. Du?an. Failure of the bucket wheel excavator buckets [J]. Eng. Fail. Anal.，2018（84）：247-261.

[15]A. Du?an，G. Neboj?a，S. Simon，A. Aleksandra，U. Milan. Integrity assessment and determination of residual fatigue life ofvital parts of bucket-wheel excavator operating under dynamicloads[J]. Eng. Fail. Anal.，2019（105）：182-195.

[16]C. J. Coetzee，D. N. J. Els. The numerical modelling of excavator bucket filling using DEM [J]. J. Terramechanics，2009（46）： 217-227.

[17]R. Eugeniusz，C. Les?aw，M. Andrzej，M. Przemys?aw，O. Jerzy，P. Damian. Investigation and modernization of buckets of surface mining machines [J]. Eng. Struct.，2015（90）：29-37.

[18]Z. Q. Fang，G. M. Hu，J. Du，et al. A method for representing structural boundaries by mathematical equations and triangular meshes in DEM simulations [J]. Int. J. Numer. Meth. Eng.，2017，111（3）：218-246.

[19]胡國明，方自強，李婉婉，等. 多球顆粒離散元仿真計算軟件[P]. 中國：2016SR154869，2016-06-24.

An Investigation on the Geometric Modeling for Structure Surface of Digging Bucket Using Elemental Spheres in the DEM Simulation

FANG Ziqiang

( School of Electromechanical and Architectural Engineering, Jianghan University, Wuhan 430056,China)

A multi-precision geometric modeling is proposed for the structure surface of digging bucket using elemental spheres. Based on the geometrical features and functionality requirements, this multi-precision geometric modeling is applied in analyzing the structure surfaces of the bottom plate, web, lateral plates, front plates and teeth in a digging bucket. Comparing the geometric models of the digging bucket with different precision, the result shows that the time consumed in the DEM simulation increases with the rise of the precision of geometric modeling for structure surface. Therefore, both the efficiency and veracity of DEM simulation should be taken into account in the geometric modeling. The comparison between our method and triangular facet method shows that the elemental spheres are able to express the local geometry characteristic of the digging bucket. It can be expected that our method takes less computational time than triangular facet method in the DEM simulation of digging process.

digging bucket；structure surface；geometric modeling；DEM simulation；elemental spheres

U294.8+8

A

10.3969/j.issn.1006-0316.2020.04.003

1006－0316 (2020) 04－0013－07

2019－12－16

湖北省自然科學基金（2019CFB208）；江漢大學高層次人才科研啟動經費（1006－06640001）

方自強（1987－），男，湖北武漢人，博士，講師，主要研究方向為顆粒系統離散元仿真技術研究與應用，fangziqiang1202@sina.com。