缺失值條件下基于LSTM單特征輸入的短波頻率預測研究

尚教凱　賀寅　徐池　徐銘

摘要：研究中發現，將短波遠程通信中兩點間的可用頻率作為單特征輸入，利用長短期記憶人工神經網絡（ISTM）可以實現對未來幾天短波頻率進行預測。該文對輸入的樣本數據存在缺失值條件下的情況進行分析，最終得到缺失值條件下該方法的應用策略，對遠程短波通信保障具有重要意義。

關鍵詞：頻率預測;LSTM;缺失值

中圖分類號：TP319 文獻標識碼：A

文章編號：1009-3044（2020）09-0251-04

1 引言

短波通信一直是海上遠程通信不可缺少的手段。科學技術的不斷進步推動著短波通信向著建鏈速度更迅捷、數據傳輸容量更大的方向發展，但實現準確的短波通信頻率預測是制約著遠程短波通信質量提升的關鍵問題。

現有的ITS-HF系列短波頻率預測軟件雖然能夠實現復雜鏈路程序化，但該系列預測軟件的輸入條件過于苛刻，且局限性較強，在實際海上通信過程中的效果并不好。而短波頻率作為典型的非線性時間序列，有很多學者基于模糊小波、神經網絡、混沌理論等算法對時間序列預測開展研究，任淑婷采用模糊小波神經網絡方法對短波頻率進行預測，預測值與實際值的相對誤差在9%左右，但工程實現難度較大。

根據深度學習擅長提取非線性時間序列數據特征的特點，通過時間半年，間隔一小時的頻率樣本數據對長短期記憶人工神經網絡（ ISTM）進行訓練，實現了對未來約20天每小時為間隔的點對點短波遠程通信頻率預測。在實際應用過程中，收集樣本數據過程中存在出現數據缺失的可能，這種情況就不能滿足預測模型對樣本數據中時間間隔為一小時的訓練需求，那么出現這種缺失值時，該模型是否還能實現頻率預測？缺失比例是否對預測結果產生影響？

為進一步明確基于LSTM實現頻率預測方法對樣本數據的需求，本文對樣本數據存在缺失值的情況進行分析。

2 LSTM模型

3 缺失值處理

數據收集過程中出現缺失值存在以下幾個原因，一是沒有歷史經歷，未積累過相關資源;二是有歷史經歷，資源積累過程中因為設備原因出現缺少丟失，比如數據未存儲成功、設備故障導致某些數據未收集或者未傳遞到數據庫中;三是出現奇異樣本，不適合被調用，處理過程中被刪除。

缺失值的處理辦法包括填充和刪除，而填充的方法包括：

1）當調用的數據集中出現缺失值時，將所有缺失值用NULL進行填充，表示該項空值，不影響使用，

2）平均值填充。用該屬性其他值的平均值對該缺失項進行填充。

3）用最可能的值填充。本系統中頻率生成子模塊能夠根據一定數量的樣本進行頻率預測，當可通頻率存在缺失時，該預測值就是最可能的值，用預測值進行填充能夠補充缺失項。

為更好地明確缺失值對基于LSTM單特征輸入實現頻率預測的影響，本文對樣本數據中缺失值的處理辦法是刪除該項的整組數據。

4 仿真模型構建

1）仿真環境

本文的仿真是在Python3.7環境下采用Python語言實現的，為滿足Python中numpy庫（Numerical Python，Python進行科學計算和大數據分析的基礎庫）導人數據要求，需要將仿真數據存儲為.csv或.xlsx格式文件。

2）仿真數據

由于數據需求量多，難以獲得能夠滿足算法訓練要求的實際數據，本文提取“亞大預測”模型預測結果中的兩點間最高可用頻率（Maximum Usable Frequency，MUF）替代短波可通頻率作為模型驗證的仿真數據。

數據由兩部分組成，一部分是由2014年8月31日0900至2015年3月1日0800的跨度半年，間隔1小時的時間，另一部分是北京市石景山區與福建省福州市臺江區兩點間通信的最高可用頻率的數值。以上兩部分組成了4368組該時刻最高可用頻率的樣本數據集合，如下表所示：

通過Python編程，在數據預處理過程中，對仿真數據進行缺失值處理，包括連續缺失、隨機缺失兩種方法，進行缺失值處理后繼續進行下一步。

3）為能夠驗證該模型的訓練效果，需要測試樣本與預測結果進行比對，因此，在仿真實現過程需要將預處理后的仿真數據劃分成訓練樣本集和測試樣本集兩部分。

4）確定能夠評估短波頻率預測效果的評價指標。這里選用均方根誤差（ RMSE）作為計算短波頻率預測值與測試值誤差的公式。

5）將整個仿真的結果可視化，便于觀察進行對比分析。這里使用Python中的matplotlib庫進行實現。

整個仿真實現流程如圖1所示：

5 仿真結果與分析

缺失值的情況分為連續缺失以及隨機缺失兩種，下面通過Python軟件對這兩種情況進行仿真，根據仿真結果進行總結分析。

5.1 連續缺失情況

在基于LSTM單特征輸入實現頻率預測的方法中，當需要調用的樣本數據集從中間部分連續缺失比例為12.5%時，運行結果如圖2所示。其中圖2（a）中的藍色部分為訓練區域，黃色部分為預測區域，橫軸代表日期，坐標間隔為1個月，縱軸代表頻率值，單位為MHz。圖2/b）中黃色線條為預測值，藍色線條為實際值.橫軸為日期，坐標間隔為6小時，縱軸為頻率值，單位為MHz。

當需要調用的樣本數據集從中間部分連續缺失比例為25%時，其預測值結果如圖3所示：

5.2 隨機缺失情況

當需要調用的樣本數據集中隨機缺失比例為1.25%時，其預測值結果如圖4所示：

當需要調用的樣本數據集中隨機缺失比例為2.5%時，其預測值結果如圖5所示：

當需要調用的樣本數據集中隨機缺失比例為15%時，其仿真結果如圖6所示：

當需要調用的樣本數據集中隨機缺失比例為20%時，其仿真結果如圖7所示：

當需要調用的樣本數據集中隨機缺失比例為25%時，其仿真結果如圖8所示：

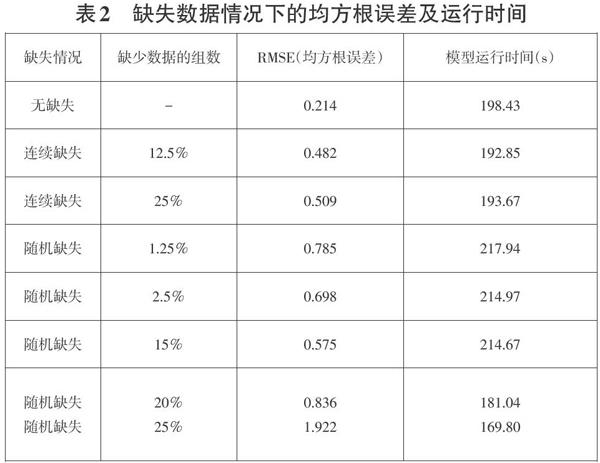
基于LSTM單特征輸入實現頻率預測方法在缺失數據情況下的均方根誤差及運行時間如表2所示：

通過對以上圖表對比分析，可以總結如下：

（l）從2（a）中可以看出兩塊藍色部分中間的白色區域為樣本數據集中缺失部分，通過圖表觀察可以發現在單特征輸入頻率預測模型中連續出現缺失值與未出現缺失值時相比RMSE值偏大，模型運行時間稍少一些，但擬合效果較好，仍能夠滿足預測精度需求。

（2）隨機缺失數據情況下RMSE值比未出現缺失值時大，隨著隨機缺失數據增多，模型運行時間減少。

（3）當隨機缺失比例達到20%開始，預測精度難以滿足通信需求，因此當可通頻率資源庫中可提供的樣本數據集中隨機缺失比例達到20%以上時，單特征輸入頻率預測模型的預測結果不可靠。

6 結語

本文通過對樣本數據中的缺失值情況進行分析，總結得出當訓練樣本數量不少于3000組，時間間隔1小時，隨機缺失比例不高于20%的條件時，基于LSTM單特征輸入模型能夠用于實現短波頻率預測。

參考文獻：

[1]賀驍，劉蕓江，肖瑤，等.基于傳播損耗的短波自適應快速建鏈[J].電訊技術，2014，54（3）：302-306.

[2]楊青彬，余毅敏，余奇，等.基于lTS軟件的短波頻率管理系統設計[J].電訊技術，2013，53（3）：249-253.

[3]田曉銘，張海勇，徐池，等.泛Kriging法在海上短波通信頻率預測中的應用[J].電訊技術，2018，58（12）：1434-1440.

[4]黃少昆，王偉民，黃子洋，等，電離層F2層臨界頻率預測方法探討[J].氣象水文裝備，2009，4（20）：19-21.

[5]簡相超，鄭君里，混沌和神經網絡相結合預測短波通信頻率參數[J].清華大學學報f自然科學版），2001，41（1）：16-19.

[6] Wang Y C.Short-term wind power forecasting by genetic algo-rithm of wavelet neural network[C]//2014 International Confer-ence on Information Science，Electronics and Electrical Engi-neering， April 26-28， 2014. Sapporo， Japan. IEEE， 2014：1752-1755，

[7]任淑婷，郭黎利.基于模糊小波神經網絡的短波頻率預測[J].通信技術，201 1，44（4）：37-39.

[8]徐池，邱楚楚，李梁，等.海上短波通信頻率優選技術現狀與分析[J].通信技術，2015，48（10）：1101-1105.

[9]尚教凱，張海勇，徐池，等.基于LSTM單特征輸入的短波可用預測研究[J].艦船電子工程，2019，39（11）：76-78，88.

[10]鄧建新，單路寶，賀德強，等.缺失數據的處理方法及其發展趨勢[J].統計與決策，2019（23）：28-34.

【通聯編輯：朱寶貴】