共線向量題型例析
■賀顯孟
共線向量也叫平行向量。利用共線向量可以證明三點(diǎn)共線、求參數(shù)的值或參數(shù)的范圍、求點(diǎn)的坐標(biāo)、求向量的坐標(biāo)以及解決與三角函數(shù)有關(guān)的問題。下面舉例分析,供大家學(xué)習(xí)與參考。
題型一:利用共線向量的概念判斷命題的真假
例1 給出下列命題:
①有向線段就是向量,向量就是有向線段;②向量a與向量b平行,則a與b的方向相同或相反;③向量與向量共線,則A,B,C,D四點(diǎn)共線;④如果a∥b,b∥c,那么a∥c;⑤兩個具有公共終點(diǎn)的向量,一定是共線向量。
以上命題中正確的個數(shù)為( )。
A.1 B.2
C.3 D .0
解:向量可以用有向線段表示,但向量不是有向線段,有向線段也不是向量,①不正確。若向量a與b中有一個為零向量,零向量的方向是不確定的,則a與b的方向不一定相同或不一定相反,②不正確。共線向量所在的直線可以重合,也可以平行,③不正確。如果b=0,則a與c不一定平行,④不正確。兩向量共線要看其方向而不是起點(diǎn)或終點(diǎn),⑤不正確。應(yīng)選D。
小結(jié):方向相同或相反的非零向量,叫作共線向量或平行向量,規(guī)定:0與任一向量共線。相等向量不僅模相等,而且方向也相同,所以相等向量一定是平行向量,而平行向量未必是相等向量。
題型二:利用共線向量證明三點(diǎn)共線
例2 已知非零向量e1,e2不共線。如果e2)。求證:A,B,D三點(diǎn)共線。
證明:因?yàn)樗韵蛄颗c共線。又向量與有公共點(diǎn)B,所以A,B,D三點(diǎn)共線。
小結(jié):證明三點(diǎn)共線,可利用向量共線來解決,但應(yīng)注意向量共線與三點(diǎn)共線的區(qū)別與聯(lián)系,當(dāng)兩個向量共線且有公共點(diǎn)時,才能得到三點(diǎn)共線。
題型三:利用向量共線求參數(shù)的值
例3 (1)已知a與-b是兩個不共線的向量,且向量a+λ b與-(b-3a)共線,則λ的值為____。
(2)已知點(diǎn)A(-1,1),點(diǎn)B(2,y),向量a=(1,2),若,則實(shí)數(shù)y的值為____。
(3)設(shè)向量a=(m,2),b=(1,m+1),且a與b的方向相反,則實(shí)數(shù)m的值為____。
解:(1)因?yàn)閍+λ b與-(b-3a)共線,所以存在實(shí)數(shù)μ,使得a+λ b=μ(3a-b)。由此可得
(3)因?yàn)橄蛄縜∥b,所以m(m+1)=2×1,解得m=-2或m=1。當(dāng)m=1時,a=(1,2),b=(1,2),a與b的方向相同,舍去;當(dāng)m=-2時,a=(-2,2),b=(1,-1),a與b的方向相反,符合題意。
故實(shí)數(shù)m=-2。
小結(jié):設(shè)向量a=(x1,y1),向量b=(x2,y2),則a∥b?a=λ b(b≠0,λ∈R);a∥b?x1y2-x2y1=0。
題型四:利用向量共線求參數(shù)的范圍
例4 如圖1所示,A,B,C是圓O上的三點(diǎn),C O的延長線與線段B A的延長線交于圓O外一點(diǎn)D,若,則m+n的取值范圍是( )。
A.(0,1)
B.(1,+∞)
C.(-∞,-1)
D.(-1,0)
解:由點(diǎn)D是圓O外一點(diǎn),可設(shè)0),則
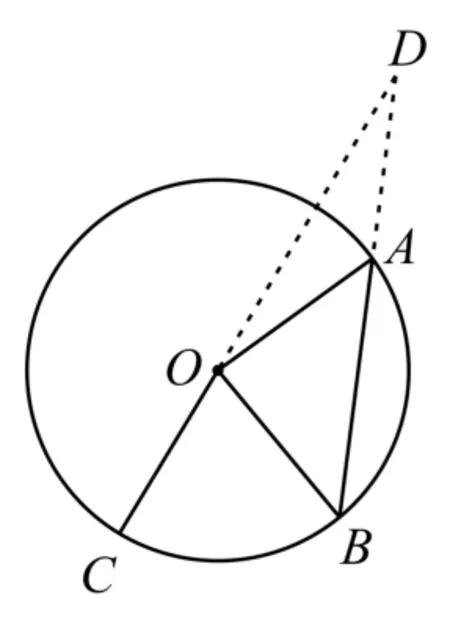
圖1
由C,O,D三點(diǎn)共線,令1),可得由上可得,所以m+n=應(yīng)選D。
小結(jié):A,P,B三點(diǎn)共線為平面內(nèi)異于A,P,B的任一點(diǎn),t為平面內(nèi)異于A,P,B的任一點(diǎn),x∈R,y∈R,x+y=1)。
題型五:利用向量共線求點(diǎn)的坐標(biāo)
例5 如圖2所示,已知點(diǎn)A(4,0),B(4,4),C(2,6),試?yán)孟蛄糠椒ㄇ缶€段A C與O B的交點(diǎn)P的坐標(biāo)。

圖2
解:設(shè)
因?yàn)榕c共線,所以(4t-4)×6-4t×(-2)=0,解得
小結(jié):向量a(a≠0)與b共線,當(dāng)且僅當(dāng)存在唯一的實(shí)數(shù)λ,使得b=λ a。若向量a=(x1,y1)與b=(x2,y2)共線,則x1y2-x2y1=0。
題型六:利用向量共線求向量的坐標(biāo)
例6 (1)已知點(diǎn)A(1,3),B(4,-1),則與向量同方向的單位向量是____。
(2)若平面向量a,b滿足|a+b|=1,a+b平行于x軸,向量b=(2,-1),則向量a=____。
解:(1)由=(4-1,-1-3)=(3,-4),可得|,所以與向量同方向的單位向量為
(2)設(shè)向量a=(x,y)。由b=(2,-1),可得a+b=(x+2,y-1)。
因?yàn)橄蛄縜+b平行于x軸,所以y-1=0,即y=1。故向量a+b=(x+2,0)。
又因?yàn)閨a+b|=1,所以|x+2|=1,可得x=-1或x=-3。
故向量a=(-1,1)或a=(-3,1)。
小結(jié):單位向量是長度(或模)等于1個單位的向量。向量坐標(biāo)的求法:①若向量的起點(diǎn)是坐標(biāo)原點(diǎn),則終點(diǎn)坐標(biāo)即為向量的坐標(biāo);②設(shè)點(diǎn)A(x1,y1),點(diǎn)B(x2,y2),則向量,向 量的長度
題型七:利用共線向量解決與三角函數(shù)有關(guān)的問題
例7 已知向量a=(1-sinθ,1),b=,若向量a∥b,則銳角θ等于( )。
A.30° B.45°
C.60° D.75°
解:由向量a∥b,可得(1-sinθ)(1+,解得又因?yàn)棣葹殇J角,所以θ=45°。應(yīng)選B。
小結(jié):平面向量作為高考的必考內(nèi)容,一直受到命題者的青睞,尤其是平面向量與三角函數(shù)有關(guān)的問題是高考的常見考點(diǎn),這類問題應(yīng)該引起同學(xué)們的重視。

