基于二維截面篩選標記的點云簡化方法研究*
劉菲菲,楊 鐸
(大連大學 機械工程學院,遼寧 大連 116622)
0 引 言
近年來,非接觸式測量方法因為其方便簡單的操作,在逆向工程領域中多有應用,尤其是在復雜曲面零件的逆向數字化掃描。
隨著電子計算能力的提高和掃描設備的高精度化,更高數量級點云在非接觸測量方法中出現,也帶來了大量噪聲和冗余數據點。為保證后續逆向工作能夠高效完成,必須做好點云的預處理。一般包括點云去噪和點云簡化兩步,先用濾波法去除有序或部分有序的大尺度噪聲干擾。
吳玉泉等[1]用空間單元格對點云進行了點云空間的有序劃分,得到了各個單元格內的“中心點”,并求出了距離標準偏差,根據設定的相應閾值進行了去噪。Rosman G[2]在標準基礎模型和距離掃描上應用補丁協同譜分析,其魯棒性較高,應對無序點云的去噪效果較差。崔鑫等人[3]提出了基于特征信息的加權模糊C均值聚類去噪算法,保持了點云本來特征,適用范圍較廣,從圖形上看模型線條略尖銳。史皓良[4]提出了基于點云曲率特征信息分類去噪法,針對兩種不同特征區域分別去噪,即鄰域距離平均濾波和自適應雙邊濾波,突出了點云主體,在特征豐富區域(角點和相交的邊界線上)有較大偏差;文獻[5]同樣是對不同尺度的噪聲進行了分步處理,結合了點云模糊均值聚類和點云雙邊濾波去噪的方法,去噪效果較佳。
由于小尺度噪聲往往不具有明顯規律,對其的處理放在點云精簡過程中。精簡的目的則是去除點云主體中的重復點和冗余點,用最少的點表示最多的信息。Shuai Yuan等人[6]認為傳統算法經常丟失幾何信息并且沒有動態擴展結構,提出了一種基于共形幾何代數的簡化算法:利用球形樹構造了多分辨率細分,利用k均值聚類計算了最小邊界球,然后用兩種具有遠程計算便利性的簡化方法進行了自我分割,適應性簡化。
近年來出現一種代替簡化法[7-8]:先基于距離的聚類算法對點云進行分類,在估計曲率較小的簇里可以用簇中心代替簇中所有點從而簡化點云。
本研究提出一種與傳統處理方式不同的點云簡化算法—二維截面篩選標記法。
1 算法設計
1.1 預處理流程
點云的預處理流程如圖1所示。

圖1 預處理流程
圖1中,直通濾波和統計濾波根據文獻[9]設置。
1.2 截面掃描法
1.2.1 坐標系轉換和選定截面
點云數據最初坐標系為局部坐標系LCS,點云坐標點用(xl,yl,zl,R,G,B)表示。用一長方形截面截取點云數據,截面所在面作為新建物體坐標系MCS中的XOY面,截面一角作為新坐標系下的原點O,其它角點坐標分別為(a,0)、(0,b)、(a,b),截面面積為ab,點云群方向為正Z軸。
在截面上點的坐標(xl,yl)根據旋轉和平移原則轉化為新坐標(xm,ym),Zl坐標不做改動。
截面選取如圖2所示。

圖2 截面選取
選取的截面向Z軸正方向每次移動z距離作為新截面,z為點之間最小平均間隔,共移動n次,共n+1張截面。n和由點云在Z方向總長度確定,使全部點云密集區被截面所截取;z由點云密度確定。為節省運算空間,點不超過5個的截面忽略不計算。每一截面轉化為新坐標系,其點隨之轉換為新坐標。設置點云截面面積大小固定,保證每一片都能將點云主體包括在內。若點云主體有需要剔除縫隙雜點的部分,在截面選取時,取能使縫隙在截面上投影面積最大的面。
1.2.2 選定掃描域
本研究在截面上取一圓形掃描域,圓心為原點坐標(xo,yo),根據計算的平均點間距[10]取圓的半徑為r(小于密集區點云平均距離),此時在直角坐標系下圓的方程為x2+y2=r2,掃描域按照設定方向運動,圓心為(xa,yb)圓的方程變為:
(x-xa)2+(y-yb)2=r2
(1)
掃描域初始運動方向如圖3所示。
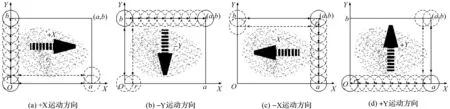
圖3 掃描域初始運動方向
4個主運動方向+X,-Y,-X,+Y分別在圖2中用箭頭標注。以圖3(a)的+X方向為例,圓的圓心從(0,0)直線運動到(a,0),觸到對邊返回或按2.2中介紹的觸點返回(0,0)點,在Y軸方向運動r距離,圓心到點(0,r),再繼續沿+X方向運動觸邊或觸點返回,至此以往到達(0,b),進入主方向-Y運動。-Y,-X,+Y方向的運動規律同理。
1.2.3 篩選和標記
目標是篩選密集區外的孤立點和密集區輪廓的邊沿非模型點,將孤立點記為A點群,能顯示輪廓的點記為B點群,白色或淺白色點即顏色坐標(R,G,B)>(250,250,250)的點標記為C點群,僅有B標記的點組成的點云即為實際輪廓組成的主要部分。

第一次觸點,I=1,此時圓心坐標為(xa1,yb1):

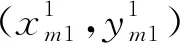
(3)N>2,N個點的排序方式同理,因為圓初始沿直線方向運動,遇到的點必然在圓的下半弧段,取使連成的弧段最長的兩個點,兩點中點與圓心連成的射線方向為掃描域的新運動方向。
掃描域改變運動方向進行第二次觸點,I=2,有以下a、b兩種情況:
(a)當第1次觸到的某點再次落在圓上,即將運動到圓外時,若圓上仍未出現新點,則將第1次觸的N個點標記為A+x,且掃描域彈回初始路徑中的截面邊繼續運動,運算下一條直線運動的觸點過程;
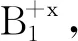
有向面積法用到向量積,順序輸入多邊形每個頂點的坐標,按同樣的順序(順時針或反時針)兩兩叉乘。多邊形面積即為向量積之和的絕對值的一半。
設多邊形由點P0,P1,…,PN-1連線圍成,則面積S為:
(2)

為降低循環次數,設置最多可觸點ε(1≤ε)次,期間若S始終小于S0,掃描域不繼續運動,返回截面邊。到下一條直線上的運動規律相同,但屏蔽截面上有標記的點,不再被圓識別,避免重復標記。掃描域從坐標原點到達截面下一角,在大方向-Y的每一條直線中繼續篩選A和B點群,當4個大方向的點群篩選完畢后,這一截面上的密集區外孤立點和輪廓均點已清晰標記。
向Z軸正方向移動z距離的新截面再次進行篩選,當n+1張截面篩選完畢后,開始點的自動剔除和手動剔除工作。
1.2.4 半自動剔除
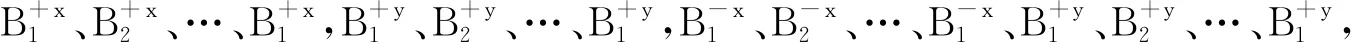
2 仿真實驗
2.1 實驗設置
為利用單目視覺技術恢復典型機械零件夾頭的點云三維模型,筆者初步重建得到點云數目為625 482。點云可分為高密度點云和低密度點云。由文獻[11]知,點云數量在一萬以內為低密度點云,如CMM測量所得;幾萬至幾千萬的點數為高密度點云,通常由光學測量法所得。本研究使用圖像掃描法三維重建設備,生成數十萬點數的中高密度點云。
其中,a方向和b方向的點云模型如圖4所示。

圖4 a方向和b方向的點云模型
零件a方向長度為50 mm,尺寸為0.2×0.2×0.2 m3。實驗裝置有柔光棚、轉臺、單反相機(佳能500D)。對夾頭拍攝144張圖片,按單目視覺原理合成零件表面輪廓的點云模型,在VC++平臺上結合OpenGL實現算法流程,通過處理點云數據包含零件位置、點的位置和顏色等信息,對模型進行濾波去噪和簡化。
2.2 實驗結果與分析
由塔型分解算法[12]計算得點云分辨率為3 μm/mm,可直接標記出C點有6 379個。為將零件的中間空洞部分篩選出更多孤立點,截面從圖3(a)中a方向從左至右運動,在物體坐標系中Z方向最長52 mm,由此計算。
根據大量實驗發現有3種因素最為影響篩選點數:截面面數n、掃描域半徑r(μm)、觸點次數I。為清晰顯示輪廓,筆者為每個因素選取5種水平,做L25(35)正交實驗,得出B標記出的孤立點數只和面數有關,因為面數越多,篩選得到的總體點數相應增加,運算時間也會增多,但較另外兩因素的對標記點數量影響較小。
固定截面面數為16 000,通過對另兩個影響因素試驗得到檢測出的輪廓點數量隨觸點次數變化規律如圖5所示。

圖5 檢測出的輪廓點數量隨觸點次數變化規律
由圖5可知,B標記的孤立點數隨I增大而增大,到一定程度檢測出的點數趨于穩定,但檢測時間和檢測誤差也相應增加。綜合運算時間和標記點數量等因素,得最佳觸點次數為4。
固定I為4,掃描域半徑分別為2.3 μm,2.5 μm,2.7 μm,2.9 μm進行簡化,檢測出的輪廓點數量隨觸點次數變化的局部簡化效果如圖6所示。

圖6 局部簡化效果圖
圖6中,隨觸點次數增加,檢測出的輪廓點數量增加,但發現其中點云模型丟失一部分關鍵特征,所以取掃描域半徑2.7 μm為最佳參數,約分辨率的0.93倍。
文獻[13]采用連續變形簡化算法來簡化點云。為驗證本文算法的有效性,筆者在Intel Core i7-6700K CPU、運行內存32GB、Windows10 64操作系統環境,于VC++平臺上結合OpenGL實現本文簡化算法中自動去除模式,處理夾頭點云模型。
同操作環境下,用連續變形法處理夾頭點云數據。筆者用兩種方法分別進行點云預處理的局部效果,如圖7所示。

圖7 兩種方法分別進行點云預處理局部效果圖
由圖7可知,夾頭夾縫內處理情況較優的是本研究方法。
處理過程記錄了運行時間并計算相關參數,筆者列成本文算法和連續變形法的客觀性能對比,如表1所示。
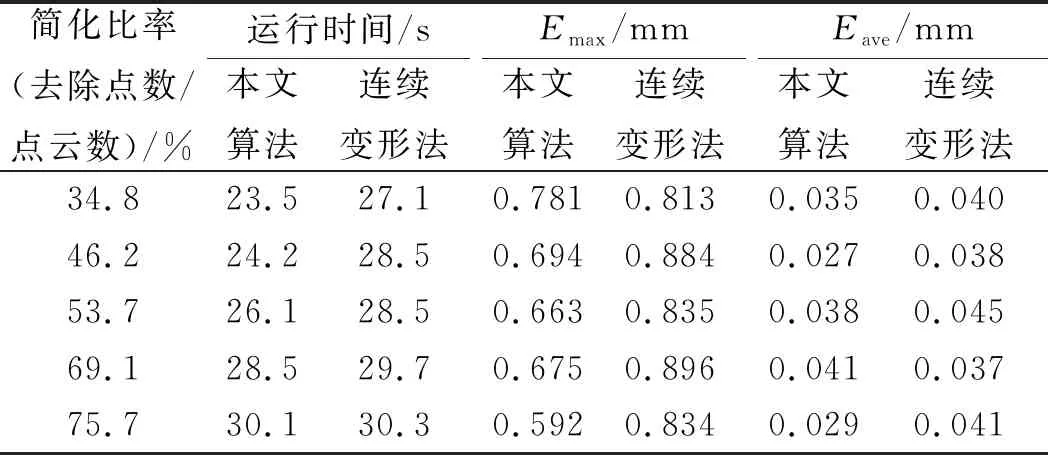
表1 本文算法和連續變形法的客觀性能對比
表1中,Emax、Eave分別為點云模型光順的最大頂點誤差和平均誤差,Emax越小說明點云質量越好;Eave反映模型整體的噪聲情況,其值越小,說明算法魯棒性越強。從表1中得出:本文算法平均Emax和Eave均低于連續變形法,在運算時間上也有優勢。
3 結束語
本研究介紹了截面篩選標記的點云簡化算法,提出了點云數據降維處理思想,強調在截面上要進行統一坐標變換,需要根據點的密集程度選取截面數量;在二維平面內處理點的位置坐標和顏色等信息。點云濾波去噪和截面篩選標記簡化相結合的方法魯棒性較好,總體運行速度滿足普遍需求,可以充分去除小尺度噪聲點和冗余點。實驗結果表明:
(1)本研究算法適應性強,與大尺度去噪的直通濾波、統計濾波及半徑濾波結合使用,可以處理同時具有多種噪聲的中高密度散亂數據點集;
(2)算法在去除噪聲的同時,良好反映物體三維特征,防止模型的過光順。
與連續變形法比較,本研究方法的三維點云數據模型整體預處理情況較好,光順誤差小。由于掃描域半徑和掃描次數等閾值的選擇需要根據點云分辨率以及實際經驗來確定,如何自適應的選擇最優參數是本研究方法今后研究的核心。

