數學例題教學研究的回顧與展望

張定強 裴凱

摘要：數學例題教學是數學課堂教學的重要組成部分，影響著數學課堂教學的成效。以中國知網收錄的與此主題相關的核心期刊論文為研究對象，采用文獻計量法與內容分析法，對其進行量化與質性分析。量化分析從發表年份、期刊來源、作者單位類型及合著情況、關注情況四個方面進行，質性分析從數學教材例題以及數學例題教學兩個層面梳理研究結果。數學例題教學研究需要立足傳統、面向世界、重視實踐，強化反思，進而找準數學例題教學研究的立足點、生長點和創新點。

關鍵詞：數學例題;例題教學;回顧展望

例題是數學教材的重要組成部分，是實現數學課程目標、實施數學教學的重要資源[1]，也是學生理解概念、原理，領悟數學思想方法的具體途徑[2]。而例題只有通過教學這一方式才能發揮其功能，例題教學則是課堂教學的重要組成部分，也是決定教學效果的關鍵環節。關于數學例題教學，自數學課程改革實施至今已有不少研究成果，本文通過對這些研究成果的整理和分析，以了解數學例題教學研究的現狀，充分認識數學例題教學研究的必要性和重要性，展望未來研究方向。

一、研究設計

本研究以“中國知網資源總庫”為文獻來源，為保證所檢索文獻的全面性與權威性，在“期刊”的高級檢索“主題”一欄中分別輸入“數學例題教學”和“數學例題”，將搜索日期限定為1999年至2018年，并且“來源類別”選定為“核心期刊”，剔除重復以及無關文獻，選取38篇文獻作為研究對象。本文以文獻計量法與內容分析法為主要研究方法。

二、研究結果

（一）量化分析結果

1.發表年份

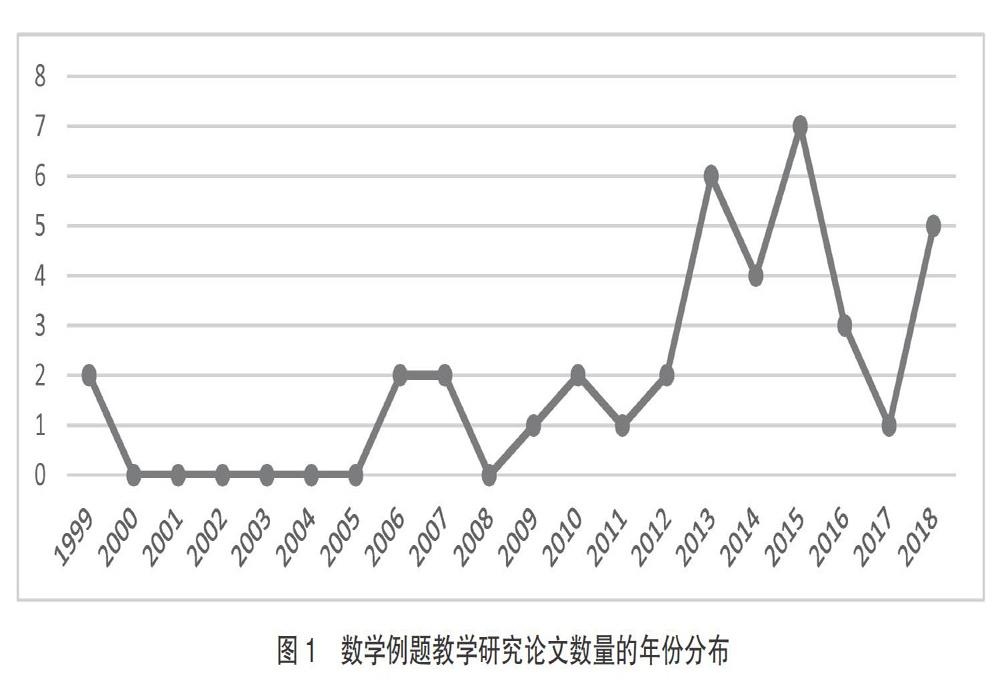
從數學例題教學研究的發文數量及年份分布，可以反映出該研究的研究現狀以及被關注程度，也可預測未來研究的發展趨勢。由圖1可以看出，1999～2018年，中文數據庫“中國知網”收錄“數學例題教學”研究的核心期刊論文數量于2015年達到峰值，其整體呈上升趨勢，局部呈波動狀，反映了數學例題教學研究近20年的基本態勢。

2.期刊來源

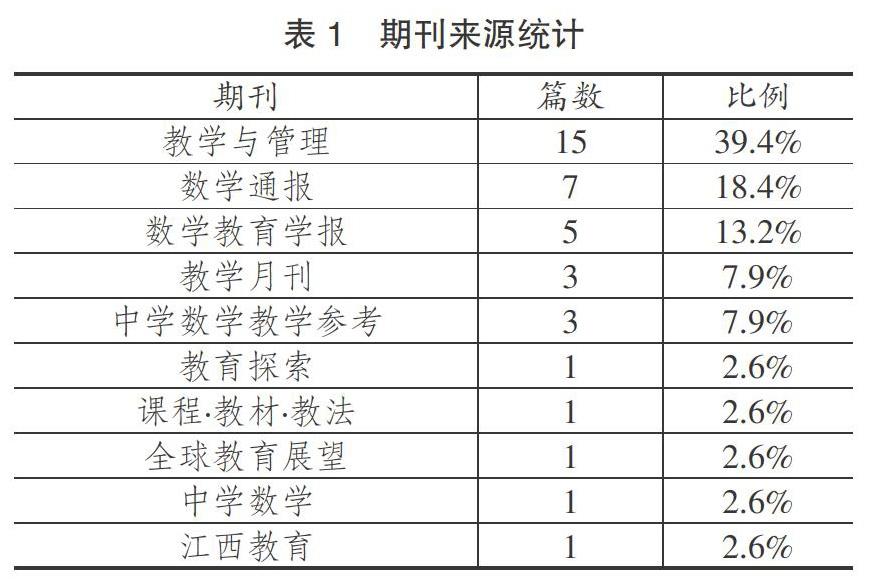
由表1可以看出，關于數學例題教學研究的論文核心期刊來源共10種，其中71%來源于《教學與管理》、《數學通報》與《數學教育學報》三種期刊。

3.作者單位類型及合著情況

作者單位類型揭示出研究該領域的主體作者分布狀況。將作者單位類型簡單劃分為中小學、高校和專門研究機構三種，論文的合著情況分為獨立撰寫與合作撰寫兩類。統計發現，中小學教師是數學例題教學研究的主力軍，有19篇是其獨立完成，占比60%，合作撰寫的論文作者單位類型大多是高校。

4.關注學段

研究對象所處學段反映了該領域研究者的關注點。統計發現，研究對象所處學段近50%集中于高中，其次是小學、初中，學前、中職或大學等其他學段均無涉及。

（二）質性分析結果

1.基于教學的數學教材例題分析

（1）功能分析

由于部分教師在實際教學中未充分認識到教材例題的價值與功能，造成教材例題無效或負效使用的現象，基于此吳立寶提出了教材例題的六大功能[3]。教材例題作為教材內容的重要組成部分，其在教材所處位置的不同，發揮的功能也有所不同。一般情況下，例題在講述完某個概念、定理后給出，一方面是因為數學概念、定理等的高度概括與抽象性，通過例題將抽象概念具體化，幫助學生初步理解和掌握;另一方面，由于概念大多是用陳述性知識和程序性知識表征，而例題是將陳述性知識程序化的體現，有助于學生認知圖式的構建及自動化[4]，這體現了例題的示范與鞏固功能，其中示范功能除了顯性層面的示范，如解題規范、解題程序等外，還有隱形層面的示范，如數學思維方法等。此外，部分新知直接以例題的形式給出，此類新知不是要求學生重點掌握的內容，是基礎知識的拓展延伸，這體現例題的展示新知功能[5]。最后部分例題在復習舊知的基礎上也為后續的新知打下基礎，體現了例題的復習功能與銜接功能。

不同類型的教材例題其教學功能也不盡相同，通過對教材例題分類剖析，可明確不同類型教材例題的功能。陸明明根據喻平教授提出的四種數學解題教學模式，將教材例題分為問題解答型和問題解決型兩類，指出問題解答型例題功能在于幫助學生將陳述性知識程序化、自動化，而問題解決型例題功能在于幫助學生獲得問題解決的策略性知識[6]。此外，以學生典型錯誤為素材的糾錯型例題，促使學生在教師引導下積極發揮自我意識和主觀能動性，促進學生對數學知識，觀念和方法的正確理解和掌握，充分發揮示錯的警示功能[7]。

綜上所述，數學教材例題有助于學生將解題過程規范化，抽象概念具體化，陳述性知識程序化，零散知識系統化，靜態知識動態化，隱形思想顯性化。研究者需以充分挖掘教材例題功能為前提，發掘數學例題教學潛能，發揮數學例題的教學價值。

（2）比較研究

練習題的配置是數學教材的重要組成部分，一定程度上反映了數學教材編寫者的價值取向與編寫風格[8]，對數學教材例題的比較研究分為編寫特色與綜合難度兩個維度。宋運明等學者對小學3個版本4～6年級數學教材例題從8個維度進行了全面分析研究，首次提出了例題編寫特色的分析框架，并在如何彰顯例題編寫特點方面提出了建議[9]。張文宇等人對海峽兩岸小學數學教材分數內容例題的整體結構和編寫特征進行比較，整體結構部分以史寧中的知識團思想為基礎，編寫特征部分則在宋運明的例題編寫特色分析框架的基礎上，借鑒朱雁、范良火的例題表征形式以及李業平的例題回答方式研究成果，結合教材特征，對其進行修改，除知識領域、情境傾向以及有無插圖三個維度外，添加例題表征方式及回答方式兩個維度[10]，如表3所示。此外，盧萍與邵光華參照練習題設置結構制定了例題設置的比較框架，從例題的淺層結構與深層結構對中德教材代數部分例題特色進行比較[11]。王曉麗，張明亮將戴再平建立的例題分類進行調整，并采用黎野平建構的分析問題3層面為研究工具，對中美初中數學教材有理數部分的例題從數量、內容、形式、背景、特征以及特色模塊進行比較研究[12]。

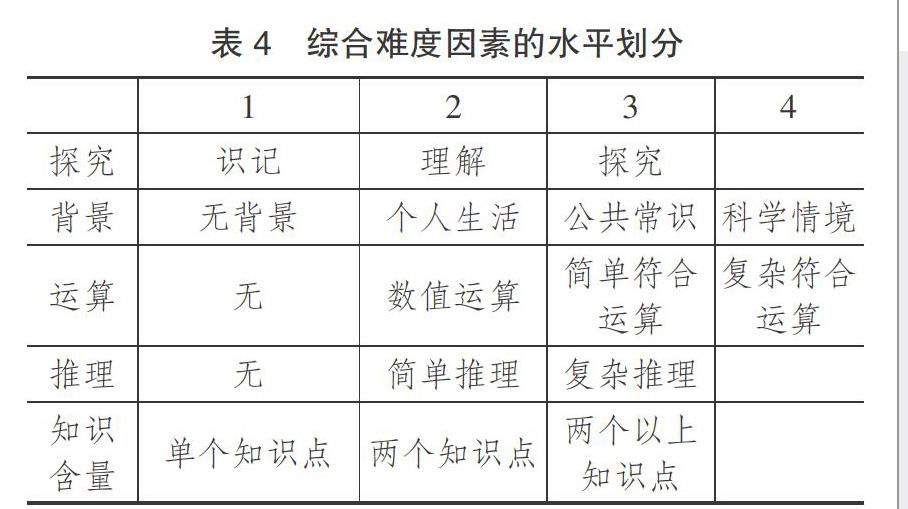
《國家中長期教育改革和發展規劃綱要（2010-2020）》提出“調整教材內容，科學設計課程難度”，于是，中小學教材的難度比較成為近年來的熱點問題，影響教材難度的因素很多，而難度水平的界定取決于所使用的評價工具[13]。鮑建生建構的五因素多水平模型長期以來被用于比較數學問題的綜合難度，如表4所示。在《高中數學教材中例題的綜合難度的國際比較》一文中對原有綜合難度模型進行修改，背景、運算、推理三個難度因素及水平劃分不變，知識含量因素名稱變為知識綜合，探究因素改為數學認知因素。另外，王曉麗，張明亮選擇鮑建生建立的綜合難度模型為研究工具之一，并根據有理數例題特點對鮑建生綜合難度模型中背景因素的劃分修改為無背景、學科相關聯、日常生活以及無實際意義四種[14]。濮安山、徐慧敏也以鮑建生的數學課程綜合難度模型為研究工具，將探究因素水平劃分為識記、理解、應用與探究，知識含量因素水平劃分為單個、兩個、三個、四個及以上[15]。

（3）二次開發

顧泠沅指出變式教學能使不同學習水平的學生都得到有效的訓練，中學數學的絕大部分基本題都可以通過適當的改造，為不同的教學目標服務[16]。動態課堂教學的有效性很大程度上取決于對靜態教材文本的正確解讀與使用，教師在潛心走進教材的同時，也要善于走出教材，做課程內容的開發創生者，通過對教材例題的有效改編，多角度、多層次地加深對課本例題的理解，進而優化課堂教學[17]。而在實際教學過程中，教師利用教材時往往存在就題論題、淺嘗輒止，也存在誤解意圖、南轅北轍的負效運用的現象，制約著課堂教學效益的提高[18]。在此背景下，研究者針對教材例題的改編做出一系列的策略研究，綜合吳成業、曹志國、汪東興等學者提出的教材例題改編策略，可以概括為“刪”“變”“拓”“調”“增”五個字。其中，“刪”指對教材例題部分條件進行適當刪減，以充分調動學生的心理需求;“變”一方面指改變數據，意在指導學生不拘泥于數據的形式，透過數據看本質，另一方面指適當變換例題素材，充分考慮時空差距與區域差異，以貼近學生生活，激發學習興趣;“拓”指對教材中例題的解題方法進行拓展，采用延遲評價方式，引導學生對多種解題方法進行比較選擇;“調”指以學生的現實認知為起點，調整教材內容的呈現方式與次序，避免循環論證與形式化的特征探究;“增”指針對教材信息呈現的留白現象，通過增設教學環節，引導學生理解學習內容本質。此外，也有教師在教學過程中發現教材例題的不足或不恰當之處，對其進行改編后取得良好的教學效果。如孔莉群教師在以課例為載體的課堂教學研究活動“磨課”過程中，充分體會到一道例題的優化過程，也是教師教學行為的調整、改進的過程，需要教師把握時機，以學生的最近發展區為前提，給予恰當的誘導，讓學生處于積極創造的過程中[19]。

另外，陸明明基于問題變式的水平、垂直變式這兩類結構，將例題變式劃分為3個層次，分別為平行變式、垂直變式與螺旋變式。其中水平變式不帶來認知負荷的變化，從垂直變式到螺旋變式，認知負荷不斷加重，3個層次的變式層層遞進，互相依存，互相補充[20]。

2.基于研究的數學例題教學探析

（1）理論探尋

樣例學習理論是數學例題教學研究的理論基礎之一，也是例題教學研究的理論支撐。樣例學習是指學習者通過研習樣例習得專家的問題解決方法的一種學習方式。在課堂實施樣例學習，需要著重關注兩類問題：一方面是樣例的設計，另一方面是如何對學生的學習過程進行指導，這兩類問題直接影響學生的學習效果[21]。

變式理論是中國數學傳統教學中十分重要的一個組成部分，核心是善于通過變化突出其中的不變因素[22]，變式理論為數學例題的變式教學提供了理論基礎。

產生式遷移理論是例題學習的理論基礎之一，規則以陳述性知識的形式進入學習者的命題網絡，然后通過變式練習轉化為以產生式表征的程序性知識。當兩項任務之間有共同的產生式或產生式的重疊式，遷移就會發生。所以，產生式的相似是遷移發生的條件，產生式自動化是順利完成復雜認知操作的基礎[22]。

在心理學上，因信息呈現的順序不同會出現首因效應，也稱“第一印象效應”，由美國心理學家洛欽斯首先提出。雖然第一印象并非總是正確的，但卻是最鮮明、最牢固的。因此，在數學教學中，課堂信息的呈現順序也會影響學生的數學思維。但教材基本上還屬于紙質為主的信息呈現媒介，編寫者無法把信息呈現意圖有效地體現在教材上，故在教學實踐中，需要教師根據具體教學情況，發揮主觀能動性[23]。

（2）實踐經驗

基于數學教育價值視角，林少安舉例闡釋了例題教學在培養探究能力、養成理性思維，弘揚文化價值以及養成良好品質四個方面的教育價值[24]，若要充分發揮數學例題教學的教育價值，首先需要認識到數學例題教學過程中存在的問題，以此為基礎，不斷改善，最終實現數學例題的有效教學。

在以往數學教學過程中，一方面課堂結構以演繹法為主，這不利于學生數學思維的形成，所以構建以歸納法為主，以演繹法為輔的課堂教學模式，充分揭示數學知識的發現過程，基本實現數學家、教師、學生思維活動的和諧統一至關重要[25]。另一方面，教學模式多采用“概念—例題—練習”，對數學思想方法的重視程度不夠，這種教學模式下的概念教學基本是一次性的，而數學概念作為數學思維的核心和邏輯起點，是數學定理、性質的邏輯基礎，故數學概念的二次教學應成為例題教學的一個環節，通過引導學生對已掌握的概念進行二次學習，挖掘概念中隱含的數學思想方法，發揮數學思想方法教學的特點與優勢[26]。而“條件+任務”是傳統數學例題的標準形態，也是長期以來數學例題的主要形式甚至唯一形式，這促成了“問題解決”的教學常態，而數學現象作為學生觀察、探究、發問的素材，沒有發揮出本身的教育價值，孫四周通過具體教學案例闡釋了基于活動與體驗的例題教學，讓學生經歷“現象—問題—解決—反思”的全過程[27]。

要實現數學例題的有效教學，首先對教材例題的二次開發是基礎，通過對教材例題適當改編，使其成為數學例題教學的原材料。其次例題教學的恰當設計是核心。再者提高學生例題學習效率是數學例題教學的根本，這就需要教師從學生的視角設計順應學生發展的例題教學[28]。最后整個教學過程的優化是關鍵，教學起點是學生認知結構中原有的知識經驗，教師需要在學生認知基礎與教學目標之間進行合理分層，增設臺階，為實現教學目標需要選取合理的教學方式，通過課堂提問，使學生暴露思維軌跡，進而對課堂生成進行合理調控，培養學生數學思維能力，故通過對教育目標的合理制定、教學起點的合理設置、教學方式的合理選擇、課堂提問的精心設計、數學思維的潛移默化、課堂生成的合理調控，進而提高例題教學的有效性[29]。

例題教學設計作為實現數學例題教學有效性的核心，一方面，數學課型不同則數學例題設計意圖不同，進而影響例題的設計策略。例如，復習課具有時間跨度大，涉及內容多，綜合性強的特點，對學生知識的遷移、查漏補缺、系統掌握以及思維能力的發展是極其重要的，所以，首先復習課例題的選取要遵循新穎性、梯度性、過程性以及關聯性的原則[30]。其次，由于思維發展的階段性特點，決定了對知識的掌握要經歷一個由淺入深、由零散到系統的螺旋上升、直至完整的過程，故復習課例題重在幫助學生認知圖式結構化、網絡化。這就需要例題教學設計時整體規劃，完善認知結構，根據知識的內容領域、知識間的區別聯系、新舊知識的生長點和連接點，運用系統論的思想，以整體規劃的眼光通盤考慮例題設計，凸顯數學知識的整體性[31]。再者，復習課需要幫助學生查缺補漏，識錯糾錯，故可設計糾錯型例題。

另一方面，數學例題教學過程中，數學例題的信息呈現方式也是影響例題教學的重要因素。根據首因效應，在不改變例題本質內容的前提下，例題條件和結論信息呈現的時間與順序會對數學教學產生不同的教學效果。楊秋紅等人將例題信息的呈現簡單劃分為“無選擇性呈現”和“選擇性呈現”兩種，其中“選擇性呈現”可進一步細分為三類，指出整體性呈現例題信息雖可以凸顯教師的主要教學意圖，但也容易忽視信息背后涉及的數學思想方法。選擇性呈現方式的思維發散度較強，但需教師根據例題本身特點、教學意圖和學情把握好發散的“度”，靈活選擇教學手段，使其具有可操作性[32]。

三、研究未來展望

1.數學例題教學研究的立足點

數學例題教學研究應立足傳統，面向世界。傳統數學例題教學理論與教學經驗是數學例題教學研究的現實“根”基，但需要辯證理順“國際化”與“本土化”的關系，反對絕對化的研究立場，運用比較、反思、混合的研究方法，不斷觸摸最新數學例題教學研究的前沿，在繼承優良研究傳統的前提下，厘清傳統數學例題教學研究的局限性，找準嘗試、調整、改善、促進數學例題教學研究的立足點。如從中國傳統例題教學重視“雙基”的培養到課改將“雙基”拓展為“四基”的研究路徑梳理，捕捉、研究數學例題教學是如何夯實“四基”的，進而探尋數學例題教學過程中如何培養和發展學生的數學核心素養。

2.數學例題教學研究的生長點

數學例題教學研究的生長點就在于數學課堂實踐。因此，要把研究的重心置于課堂教學，分析數學例題在整體課堂教學中的地位與作用，探析例題與概念、命題、原理、思想、方法之間的內在關系，特別是基于數學文化的視角探析例題教學的生長點。視數學課堂教學為其實驗田，運用科學的工具、方法、手段來探視例題教學發展學習共同體數學素養的功能價值，強調數學例題教學的微型調查、微型實驗、微型分析、微型改進，以診斷分析課堂教學中的例題教學問題。珍視每一次課堂教學中例題的嵌入、導引、分析、探究、反思過程，把數學例題教學研究的生長點置于數學課堂教學中。

3.數學例題教學研究的創新點

數學例題教學研究要發揮其功能價值，就要在理論與實踐創新上下功夫。首先，數學例題教學是數學教學理論探索的一個重要方面，一定不同于其他學科的例題教學，需要運用新的技術和手段來探索例題在不同的課型、不同的時空、不同的共同體學習過程中表現的不同形態，運用教育學、心理學、信息學等理論來探析數學例題教學的機制與運行策略，特別是要綜合眾多已有的研究成果，創新性地探索例題教學中的投入與產出、情感與價值、理性與感性、限度與發展等問題。數學例題教學研究的創新一定是繼承基礎上的創新，要全面梳理數學情境教學、參與式教學、變式教學、問題鏈教學、自學輔導教學等例題教學環節中的優勢與不足，充分地研究在情境與問題、知識與技能、思維與表達、交流與反思中數學例題存在之根、教學之徑，不斷深度研究數學例題教學與數學教學模式創新之間的關系，助推數學教學變革，全面提升學生的數學思維品質與關鍵能力。

課改歷經20年，數學例題教學研究取得了不少研究成果。要以此為基礎，站在前人的肩膀上，繼續探索數學例題教學的理論基礎，用更加全面、細致、系統的觀點直面現實問題，牢記數學例題教學的使命與擔當，不斷深入地去學習、去實踐、去觀察，開拓數學例題教學研究新天地。

參考文獻：

[1]中華人民共和國教育部制定.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社， 2011：59.

[2][13]王建磐，鮑建生.高中數學教材中例題的綜合難度的國際比較[J].全球教育展望， 2014（8）：101-110.

[3][5]吳立寶，王富英，秦華.數學教材例題功能的分析[J].數學通報， 2013（3）：18-20，23.

[4]吳立寶，秦華.例談中學數學教材例題的功能[J].教學與管理， 2013（4）：53-55.

[6][20][22]陸明明.數學教材例題的分類及其教學建議[J].數學教育學報， 2018（2）：54-58，102.

[7]朱建明.數學教學中糾錯型例題的設計與實踐[J].教學與管理， 2016（16）：60-61.

[8][15]濮安山，徐慧敏.PEP（A）版與IBID版數學教材中平面向量例題難度的比較[J].數學教育學報， 2016（3）：10-13.

[9]宋運明，李明振，李鵬，宋乃慶.小學數學教材例題編寫特點研究[J].課程·教材·教法， 2014（2）：47-51.

[10]張文宇，張守波.海峽兩岸小學數學教材分數內容例題的比較研究[J].數學教育學報， 2015（3）：68-72.

[11]盧萍，邵光華.中德代數教材例題特色比較及啟示——以“指數函數和對數函數”為例[J].數學通報， 2015（2）：21-24，39.

[12][14]王曉麗，張明亮.中美初中數學教材有理數例題的比較研究[J].數學教育學報， 2018（6）：67-71.

[16][19]孔莉群.四位數學老師和一道典型例題[J].中學數學教學參考， 2006（11）：47-48.

[17]曹志國.小學數學教材例題的有效改編[J].教學與管理， 2014（17）：43-45.

[18]汪東興.小學數學教材例題的有效利用[J].教學與管理， 2018（20）：46-49.

[21]許志毅，王英豪.樣例學習的理論與實施[J].現代教育科學， 2009（6）：46-47.

[22]鄭毓信.變式理論與認知發展[J].中學數學月刊， 2009（10）：1-4.

[23][32]楊秋紅，方均斌.數學例題的信息呈現方式及其教育功能的發掘——以一道不等式證明題為例[J].數學通報， 2013（12）：35-38.

[24]林少安.基于數學教育價值視角下的例題教學[J].教學月刊·中學版（教學參考）， 2014（7）：24-27.

[25]周洪兆.數學例題教學中培養學生歸納思想應注意的幾個問題[J].教學與管理， 2010（13）：60-61.

[26]梁棟，朱鴻玲.數學概念二次教學的實踐與思考——以一道例題的教學為例[J].數學教育學報， 2015（2）：83-87.

[27]孫四周.把數學問題還原為數學現象——談“基于活動與體驗的例題教學”[J].數學通報， 2015（10）：41-45.

[28]于正軍.例談基于“兒童視角”的小學數學例題教學[J].教學與管理， 2015（8）：42-44.

[29]蘇建強.優化教學過程，提高例題教學的有效性[J].中學數學教學參考， 2007（18）：9-10.

[30]潘振嶸.如何提高高三數學復習中例題教學的有效性[J].數學通報， 2010（10）：10-12.

[31]汪東興.小學畢業班數學總復習的例題設計[J].教學與管理， 2017（32）：45-47.

責任編輯：顏瑩