例析求解平拋運動常見問題的常用方法

■江西省南康中學

平拋運動是運動合成與分解的典型應用，也是重要的考點和命題熱點。與平拋運動相關的常見問題，有直接運用平拋運動規律的問題，也有平拋運動與圓周運動相組合的問題，還有平拋運動與天體運動相組合的問題，求解這些問題往往需要靈活運用動能定理、機械能守恒定律和能量守恒定律等。下面通過實例剖析求解平拋運動常見問題的常用方法。

一、直接運用平拋運動規律的問題

處理平拋運動時，一般將運動沿初速度方向和重力方向進行分解，按照分運動規律列式，另外需要挖掘和利用好合運動、分運動及題設情景之間的幾何關系。遇到直接運用平拋運動規律的問題時，需要關注平拋運動的時間，判斷是分解位移還是分解速度，確定平拋運動的速度偏向角、位移偏向角和兩者間的關系，靈活應用軌跡方程列式求解。

例1如圖1所示，墻壁上落有兩只飛鏢，它們是從同一位置水平射出的，飛鏢A與豎直墻壁成53°角，飛鏢B與豎直墻壁成37°角，兩者落點間的距離為d，假設飛鏢的運動是平拋運動。求飛鏢射出點離墻壁的水平距離。（sin53°=0.8，cos53°=0.6）。

解析

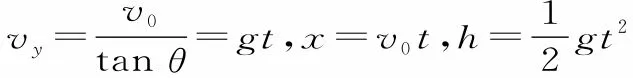
點評：本題中飛鏢的運動是平拋運動，在水平方向上的運動受到空間的約束，因此飛鏢的運動時間由沿水平方向的分運動決定，可以根據x=v0t表示出運動時間，再用時間表示出豎直方向上的分位移，根據兩飛鏢的豎直距離之差等于d，即可求解水平距離。

例2如圖2所示，A、B兩小球用長l=5 m的細線相連，先后將兩小球從平臺的邊緣相隔Δt=0.4s時間水平拋出，兩小球被拋出時的速度均為v0=7.5m/s，問：在小球A被拋出后多長時間A、B兩小球之間的細線正好被拉直？（取重力加速度g=10m/s2）。

解析

小球B剛要被拋出時，小球A發生位移的水平分量x=v0·Δt=3 m，豎直分量，兩小球之間的距離，表明小球B被拋出一段時間后細線才能被拉直。假設小球B被拋出后經過時間t細線被拉直，小球A發生位移的水平分量xA=v0（t+Δt），豎直分量，小球B發生位移的水平分量xB=v0t，豎直分量。在水平方向上兩小球之間的距離Δx=xA-xB=3m，根據勾股定理可知，在豎直方向上兩小球之間的距離，又有Δy=yA-yB，解得t=0.8s。因此小球A被拋出后經過1.2s時間A、B兩小球之間的細線正好被拉直。

點評：本題中兩小球相隔0.4s以相同的初速度拋出，兩小球在水平方向上的位移差恒定，因此可以對小球運動的位移進行分解。若突出落點問題時，一般要通過建立水平位移和豎直位移之間的關系列式求解。

例3從空中同一點沿水平方向同時拋出兩個小球，它們的初速度大小分別為v1和v2，初速度方向相反，重力加速度為g，經過多長時間兩小球速度之間的夾角為90°？

點評：求解本題時，先利用平拋運動任意時刻的兩個分速度與合速度構成的矢量直角三角形，分別對兩小球構建速度矢量直角三角形，再利用兩小球速度偏向角之間的關系和三角函數知識即可順利求得時間。若問題中突出末速度的大小和方向時，一般要通過建立水平速度和豎直速度之間的關系列式求解。

例4從高為H的A點平拋一物體，其水平射程為2s，在A點正上方高為2H的B點，向同一方向平拋另一物體，其水平射程為s。兩物體的運動軌跡在同一豎直平面內且都恰好從同一屏的頂端擦過，求屏的高度。

解析

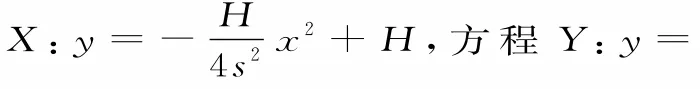
點評：若平拋運動中多次用到分位移x和y，則一般可以考慮用平拋運動軌跡方程解決。注意在應用平拋運動軌跡方程解題時，要記清平拋運動軌跡方程為。

二、平拋運動與圓周運動相組合的問題

解決平拋運動與圓周運動相組合的問題時，需要獨立用好平拋運動和圓周運動的知識，并重視兩種運動銜接處的物理量之間的聯系，還需要用好動能定理、機械能守恒定律或能量守恒定律等。

例5如圖5所示，餐桌中心是一個半徑r=1.5 m的圓盤，圓盤可繞中心軸轉動，近似認為圓盤與餐桌在同一水平面內且兩者之間的間隙可忽略不計。已知放置在圓盤邊緣的小物體與圓盤之間的動摩擦因數μ1=0.6，與餐桌之間的動摩擦因數μ2=0.225，餐桌離地高度h=0.8m。設小物體與圓盤、餐桌之間的最大靜摩擦力都等于滑動摩擦力，小物體可視為質點，取重力加速度g=10m/s2。

（1）為使小物體不滑到餐桌上，圓盤的角速度ω的最大值為多少？

（2）緩慢增大圓盤的角速度，小物體從圓盤上甩出，為使小物體不滑落到地面上，餐桌半徑R的最小值為多大？

（1）當小物體在圓盤上隨圓盤一起轉動時，圓盤對小物體的靜摩擦力提供向心力，隨著圓盤轉速的增大，小物體受到的靜摩擦力增大。當靜摩擦力達到最大時，小物體即將滑落，此時圓盤的角速度達到最大，則fmax=μ1N=mω2r，N=mg，解得ω=2rad/s。

（2）當小物體滑到餐桌邊緣速度恰好減為零時，對應的餐桌半徑取最小值。設小物體在餐桌上滑動的位移為s，小物體在餐桌上做勻減速運動的加速度大小為a，則f=μ2mg=ma，解得a=2.25m/s2，小物體在餐桌上滑動的初速度v0=ωr=3m/s。由運動學公式得v2t-v20=-2as，解得s=2 m。由幾何關系可知，餐桌半徑的最小值。

（3）小物體滑離餐桌后做平拋運動，平拋的初速度為小物體在餐桌上滑動的末速度v1′，由運動學公式得，由幾何關系得，解得v1′=1.5m/s。設小物體做平拋運動的時間為t，則，解得t=0.4s。因此小物體做平拋運動的水平位移sx=v1′t=0.6 m，由幾何關系得L=s′+sx=2.1m。

點評：小物體在圓盤上隨圓盤一起轉動時，根據小物體受到的最大靜摩擦力提供向心力可求得圓盤的最大角速度。小物體從圓盤上甩出后在餐桌上做勻減速運動，根據運動學公式可求得通過的位移，利用幾何關系可求得餐桌的最小半徑。小物體滑離餐桌后做平拋運動，根據運動學公式可求得脫離餐桌時的速度，根據運動學公式和幾何關系可求得落地點與從圓盤上甩出時的位置間的水平距離L。

例6如圖6所示，一個質量為m的小球（可視為質點）以某一初速度v0從A點水平拋出，恰好從圓管BCD的B點沿切線方向進入圓管，從圓管BCD的最高點D射出，恰好又落到B點。已知A點與D點在同一水平線上，圓弧BC所對圓心角θ=60°，重力加速度為g，不計空氣阻力。求：

（1）圓管BCD的半徑R的大小。

（2）在D點管壁對小球的彈力N。

（3）小球在圓管BCD中運動時克服阻力做的功W阻。

本文設計了以可調衰減器和定向耦合器為核心器件的發射機互調發射測量鏈路，建立了基于衰減量調節的互調發射抑制比測量方法，并以某型電臺為實驗對象，對fc=|ft±fj|、fc=|2ft±fj|、fc=|3ft±fj|、fc=|2ft±2fj|和fc=|2fj±ft|等10種互調發射類型的互調發射抑制比進行了測量.所有測量結果均符合本文的分析結論，說明本文提出的測量方法是合理可行，測量結果準確可信.

點評：小球先做平拋運動，后做豎直面內的變速圓周運動，最后又做平拋運動，這是一個平拋運動與圓周運動多過程的組合問題。用好平拋運動的規律，抓住“小球從圓管BCD的B點沿切線方向進入圓管”這一條件，對小球到達B點時的速度進行分解，即可求得R。分析小球在最高點D時的受力情況，利用向心力公式即可求得N。選取合適的運動過程，利用動能定理即可求得W阻。

例7如圖7所示，半徑為R的光滑半圓槽豎直固定在水平地面上，可視為質點的小球以大小為4m/s的初速度向左進入半圓槽，小球通過最高點后做平拋運動。若小球做平拋運動有最大水平位移，取重力加速度g=10m/s2，則下列說法中正確的是（ ）。

A.最大水平位移為1.2m

B.當R=0.3 m時，小球做平拋運動的水平位移最大

C.小球落地時，速度方向與水平地面成45°角

D.小球落地時的速度大小為4m/s

答案：CD

點評：小球先在光滑半圓槽上做變速圓周運動，再做平拋運動。利用機械能守恒定律可求出小球做平拋運動的初速度，利用平拋運動規律可以把水平位移表示出來，利用二次函數可求出水平位移的最大值。

三、平拋運動與天體運動相組合的問題

解決物體在星球表面做平拋運動的問題時，需要抓住平拋運動的加速度等于重力加速度這一條件，熟練運用運動的分解法處理平拋運動，再靈活選用天體運動相關知識求解各物理量。

例8假設一航天員站在一星球表面上的某高度處，沿水平方向拋出一個小球，經過時間t，小球落到星球表面，測得拋出點與落地點之間的距離為l。若將小球拋出時的初速度增大到原來的2倍，則拋出點與落地點之間的距離為。已知兩落地點在同一水平面上，該星球的半徑為R，引力常量為G，求該星球的第一宇宙速度的大小。

點評：根據兩次平拋運動的位移關系可求出小球做平拋運動的高度h，利用萬有引力定律相關公式可確定重力加速度g′，依據物體繞星體做圓周運動向心力的供需關系可求出第一宇宙速度v1。

感悟與提高

1.在離地面某高處，第一次將小球以初速度v0水平拋出，第二次沿著小球在空中的運動軌跡設置一條光滑軌道，改為將小球在此軌道上與第一次同一高度由靜止釋放。已知小球在運動過程中始終不脫離軌道，不計空氣阻力。比較兩次小球的運動，以下說法中正確的是（ ）。

A.運動時間相等

B.著地時的速度大小相等

C.著地時的速度方向相同

D.在豎直方向上的分運動都是自由落體運動

2.車手要駕駛一輛汽車飛越寬度為d的河流，在河岸左側建起如圖9所示的高為h、傾角為α的斜坡，車手駕車從河岸左側沖上斜坡并從頂端飛出，接著無碰撞地落在右側高為H、傾角為θ的斜坡上，順利完成了飛越。已知h＞H，當地的重力加速度為g，汽車可看成質點，忽略汽車在空中運動時所受的空氣阻力，根據題設條件可以確定（ ）。

A.汽車在左側斜坡上加速的時間t

B.汽車離開左側斜坡時的動能Ek

C.汽車在空中飛行的最大高度Hmax

D.兩斜坡的傾角滿足α＜θ

3.如圖10所示，在豎直放置的半圓形容器的中心O點分別以水平初速度v1、v2拋出兩個小球（可視為質點），最終它們分別落在圓弧上的A點和B點。已知OA與OB互相垂直，且OA與豎直方向成α角，則兩小球的初速度大小之比為（ ）。

4.一根長為0.8 m的繩子，當受到7.84N的拉力時即被拉斷，若在此繩的一端拴一個質量為0.4kg的物體，使物體以繩子的另一端為圓心在豎直面內做圓周運動，當物體運動到最低點時繩子斷裂（取重力加速度g=9.8m/s2）。求：

（1）物體運動至最低點時的角速度和線速度各是多大？

（2）若繩子斷裂時物體距地面高4.9 m，則經多長時間物體落至地面？

（3）物體落地處距拋出點的水平距離多大？落地時物體的速度多大？

5.如 圖11所示，位于豎直平面內的光滑軌道由四分之一圓弧AB和拋物線BC組成，圓弧半徑OA水平，B點為拋物線頂點。已知圖中h=2m，，取重力加速度g=10m/s2。

（1）一小環套在軌道上從A點由靜止滑下，當它在BC段上運動時，與軌道之間無相互作用力，求圓弧AB的半徑。

（2）若小環因微小擾動從B點由靜止而開始滑下，求小環到達C點時速度的水平分量的大小。

6.在21世紀，我國適時地啟動了嫦娥工程，開展了深空探測活動，為我國的航天事業創立了新的里程碑。嫦娥工程分為“無人月球探測”“載人登月”和“建立月球基地”三個階段。假設某航天員登月后站在距月球表面h高度處，以初速度v0沿水平方向拋出一個小球，經過時間t小球落到月球表面上。已知月球的半徑為R，引力常量為G。求：

（1）月球表面的重力加速度g。

（2）小球落地時的速度v。

（3）月球的第一宇宙速度v1。

參考答案：1.C 2.CD 3.C

4.（1）ω=3.5rad/s，v=2.8 m/s；（2）t=1s；（3）x=2.8m，v′=10.19m/s。