圓周運動問題的求解策略
■河南省平頂山市第一中學
圓周運動包含水平面內的勻速圓周運動和豎直面內的變速圓周運動兩類模型,求解圓周運動問題不僅需要熟練掌握圓周運動相關概念、規律和公式,還需要靈活選用解題技巧和方法。下面舉例分析。
一、水平面內圓周運動問題的求解策略
1.明確運動形式:研究對象在水平面內沿圓周做速度大小不變的運動。
2.確定向心力來源:向心力是按力的作用效果命名的,可以是重力、彈力、摩擦力等各種力,也可以是幾個力的合力或某個力的分力。在勻速圓周運動中,向心力是由物體受到的合外力來提供的,它只能改變速度的方向,不能改變速度的大小。向心力是變力,其大小。
3.正確進行受力分析:沿半徑方向和垂直于半徑方向將研究對象受到的各力進行分解,根據牛頓第二定律和向心力公式列方程。
4.合理選擇過程分析:根據題意選擇滿足動能定理或機械能守恒定律的運動過程,應用動能定理或機械能守恒定律將初、末兩個狀態聯系起來列方程求解。
例1如圖1甲所示,一質量為m的小球系在兩根不可伸長的輕繩a、b一端,兩輕繩的另一端拴接在豎直桿上的A、B兩點上。當兩輕繩伸直時,輕繩a與豎直桿間的夾角θ=30°,輕繩b水平,如圖1乙所示。已知輕繩a的長度為2L。豎直桿以自己為軸轉動,在其角速度ω從零開始緩慢增大的過程中(不同ω對應的軌跡可看成是穩定的圓周運動軌跡),下列說法正確的是( )。
A.從開始至輕繩b伸直但不提供拉力時,輕繩a對小球做的功為0
B.從開始至輕繩b伸直但不提供拉力時,小球的動能增加了
C.從開始至輕繩b伸直但不提供拉力時,輕繩a對小球做的功為
答案:BC
點評:從開始至輕繩b伸直但不提供拉力,輕繩a對小球要做功。因為圓周運動的軌跡發生變化,輕繩a的拉力為變力,所以可以先根據牛頓第二定律和向心力公式求出輕繩b剛要伸直時小球的速度,再根據動能定理求得輕繩a對小球做的功。根據角速度與速度的關系分析輕繩b剛要伸直時小球的角速度,進而可判斷出當時輕繩b是否伸直。
二、豎直面內圓周運動問題的求解策略
1.明確物理模型:判斷是輕繩模型還是輕桿模型。
3.確定研究狀態:在高中階段研究的豎直平面內的圓周運動只涉及最高點和最低點的運動情況。
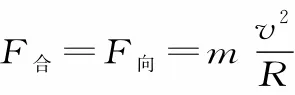
5.合理選擇過程分析:根據題意選擇滿足動能定理或機械能守恒定律的運動過程,應用動能定理或機械能守恒定律將初、末兩個狀態聯系起來列方程求解。
例2如圖2所示,細線的一端系一質量為m的小球,以另一端O為圓心,使小球在豎直面內做半徑為R的圓周運動。若小球在豎直向上方向上受到恒力F的作用,為使小球能做完整的圓周運動,在最低點B小球至少應有多大的初速度?
解析
小球在運動過程中,受到重力mg、拉力T和恒力F三個力的作用。根據重力mg和恒力F的大小關系分兩種情況討論。
(1)若F<mg,則物理上的最高點與幾何上的最高點重合,為A點。設小球能通過A點的臨界速度為vA,由牛頓第二定律和向心力公式得,解得。對小球從B點運動到A點的過程應用動能定理得。
(2)若F>mg,則物理上的最高點是B點。設小球能通過B點的臨界速度為vB,由牛頓第二定律和向心力公式得,解得。
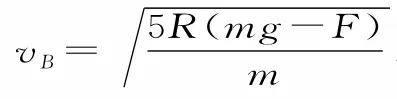
例3一內壁光滑的環形細圓管位于豎直平面內,環的半徑為R(比細管的內徑大得多),圓管中有兩個直徑比細管內徑略小的小球A、B(可視為質點)。小球A的質量為m1,小球B的質量為m2,它們沿環形細圓管順時針運動,經過最低點時的速度都為v0。設小球A運動到最低點時,小球B恰好運動到最高點,若要此時兩小球作用于圓管的合力為零,請寫出用m1、m2、R來表示v0的關系式。
解析
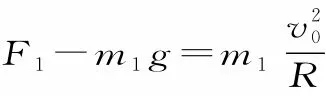
點評:本題涉及的物理模型是輕桿模型,但是題目的設問“不按常理出牌”,要求考生根據題目所給條件寫出m1、m2、R來表示v0的關系式,有的同學看到題目就會有無從下手的感覺,導致直接放棄求解。
感悟與提高
1.如圖4所示,一個內壁光滑的圓錐形筒的軸線垂直于水平面,圓錐形筒固定不動,有兩個質量相等的小球A和B緊貼著內壁分別在圖中所示的水平面內做勻速圓周運動,則以下說法中正確的是( )。
A.小球A的角速度等于小球B的角速度
B.小球A的線速度大于小球B的線速度
C.小球A的運動周期小于小球B的運動周期
D.小球A對筒壁的壓力大于小球B對筒壁的壓力
2.如圖5所示,半徑為R的光滑球體固定在水平面上,從球體的最高點A由靜止釋放一個質量為M的小滑塊,求小滑塊在下滑過程中離開球體時的位置和速率。
3.如圖6所示,輕桿OA的長度l=0.5 m,A端固定一質量m=3kg的小球,小球以O點為圓心在豎直平面內做圓周運動,取重力加速度g=10 m/s2。當小球通過最高點的速率為2m/s時,求輕桿OA受到的力。
參考答案:1.B
3.輕桿OA受到大小為6N的壓力。

