錯因促分析,探索建模型
——以“簡單的線性規劃問題(一)”教學為例
浙江省玉環中學 (317600) 李林靜
一、引言
“簡單的線性規劃問題”是人教版《普通高中課程標準實驗教科書·數學5》第三章教學內容的一部分,該課教學分3課時,本課是第一課時,主要目的是讓學生體會數學知識形成過程中所蘊涵的數學思想和方法,掌握處理代數問題的幾何方法,體會不等式是解決實際問題的重要數學模型和有效工具,形成良好的思維方式.學習本課之前,學生已掌握不等式的代數解法,及不等式的幾何意義,為本節課幾何方法作好了鋪墊.為此在教學策略上采用問題導向,問題研討,問題解決等方式實現知識的遷移拓展應用.本課教學目標是了解線性規劃的意義及線性規劃相關概念;能夠正確運用圖解法求解簡單的線性規劃問題;培養學生觀察、聯想及作圖能力,從中滲透數形結合、轉化與化歸、數學建模等數學思想.
二、教學過程
1.呈現背景,提出問題
引例已知實數x,y滿足不等式組
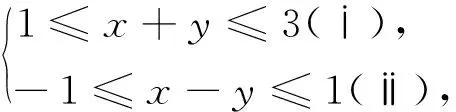

圖1
生1:式[(ⅰ)+(ⅱ)]÷2,得0≤x≤2;式[(ⅰ)+(-1)×(ⅱ)]÷2,得0≤y≤2.
生2:畫出不等式組所表示的平面區域(圖1),得0≤x≤2,0≤y≤2.
設計意圖:通過讓學生求解x,y的取值范圍,鞏固前面不等式的相關性質及二元一次不等式(組)與平面區域,分別從代數與幾何角度(圖解法)進行求解,建構起知識間聯系的橋梁,體會數形結合的思想.
(3)4x+2y的取值范圍是.
生3:式(ⅰ)×3+(ⅱ),得2≤4x+2y≤10.
生4:在(1)(2)基礎上得0≤4x≤8,0≤2y≤4,兩不等式相加得0≤4x+2y≤12.
師:為什么兩位同學解出的答案不一樣呢?
設計意圖:問題引導,激發學生尋找原因,引出下面內容:聯想激活,尋求方法.一聯想前面學過的知識,從代數角度找原因;二引導學生從幾何角度尋方法,引出本課課題:簡單的線性規劃問題(1)——錯在哪兒.
2.聯想激活,尋求方法
生5:學生4的方法最值取不到,當最大值為12時,x=2,y=2,與已知不等式組中x,y不能同時取到2矛盾,x,y是相互約束的.(鞏固取最值時要驗證等號是否成立,同時為引出線性規劃相關概念作鋪墊.)
師:剛才同學們從代數角度進行了分析,能否從幾何角度再來分析下原因呢?
提示:同學3是圖1條件求解的,同學4是在哪個條件下求解的?請畫出該平面區域,并比較兩個平面區域來進行錯因分析.
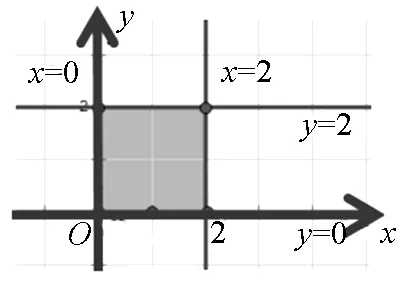
圖2
設計意圖:通過問題導向驅動學生既要會從數的角度分析,也要會從形的角度進行更直觀的分析,充分體會數形結合思想在高中數學中的重要性.
師:如何從幾何角度(圖解法)求解4x+2y的取值范圍?
在此之前,先補充線性規劃的相關概念:
(1)由x,y的不等式(或方程)組成的不等式組稱為x,y的約束條件;
(2)關于x,y的一次不等式(或方程)組成的不等式組稱為x,y的線性約束條件;
(3)滿足線性約束條件的解(x,y)稱為可行解;
(4)所有可行解組成的集合稱為可行域;
(5)關于x,y的一次目標函數稱為線性目標函數;
(6)使目標函數取得最大值或最小值的可行解稱為最優解;
(7)求線性目標函數在線性約束條件下的最大值或最小值問題稱為線性規劃問題.
師:目標函數4x+2y的幾何意義是什么?
設計意圖:鼓勵學生展開聯想,與直線聯系起來,引出第三部分:提出猜想,驗證猜想.
3.提出猜想,驗證猜想
生7:直線;
師:直線是方程式,而4x+2y是什么?
生8:代數式;
師:怎樣把目標函數寫成方程式?
生9:令z=4x+2y,這樣就變成了方程式,從而幾何意義就是直線.
師:直線z=4x+2y中z的幾何意義是什么?
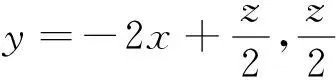
生11:所有這些直線都平行.
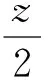
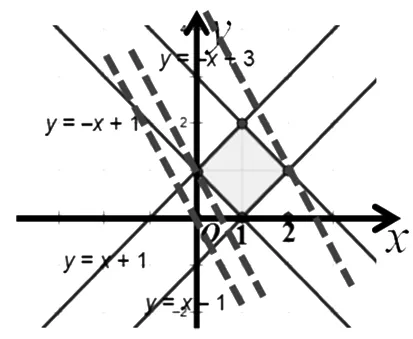
圖3
師:不妨動手多畫幾條直線z=4x+2y,觀察一下.
生13:如圖3,把這些平行線進行平移,發現在左頂點(0,1)處縱截距有最小值1,即z的最小值為2;在右頂點(2,1)處縱截距有最大值5,即z的最大值為10.
師:在畫直線z=4x+2y時,需要畫很多條嗎?能否簡潔一些?
生14:只需先畫z=0時的直線,然后經過平移求出其最優解,代入即可得出其最值.
師:是否一定是在最高點處有最值?為什么?
生15:不一定,這與直線的斜率有關系.
師:是否存在x,y,使得z=4x+2y=12?
生16:不存在,因為取定的z必須滿足直線z=4x+2y與可行域有公共點.
師:請總結圖解法解線性規劃問題的一般步驟.
生17:①畫出可行域;②畫目標函數z=Ax+By=0時的直線,利用平移的方法找出與可行域有公共點且縱截距最大、最小的直線;③根據平移結果,先求區域內特殊點的坐標,再求最優解,最后代入目標函數求出最值.
師:簡寫為:畫、移、求.這樣我們分別從數與形兩方面分別對目標函數4x+2y的取值范圍進行了求解,并總結出了圖解法求解線性規劃問題的一般步驟;但這里要關注z的幾何意義(z與縱截距的相關性),以及最優解不一定在可行域的上下兩頂點取到.
師:剛才有同學提出在最高點(1,2)處取到最值,那請同學們自己設計一個目標函數,使得該目標函數在點(1,2)處取到最大值.
生18:目標函數z=x+3y在點(1,2)處取到最大值.
師:還有其他不一樣的目標函數嗎?
生19:其實這樣的目標函數有很多,只要讓斜率k滿足|k|<1,這個范圍內的所有目標函數z=kx+y都可以.
師:能分析下原因嗎?
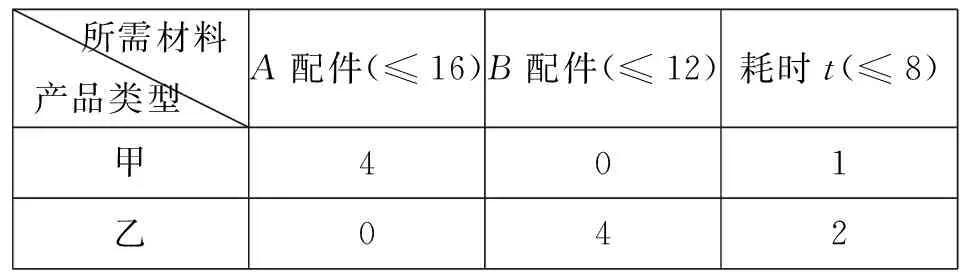
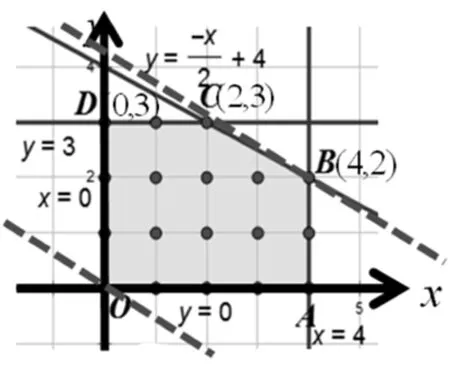
生20:可以設目標函數z=kx+y,經過變形得y=-kx+z,先畫y=-kx,經平移及旋轉發現,當-k>1時,在點(0,1)處取到最大值;當-k<-1時,在點(2,1)處取到最大值,所以-1<-k<1,即-1 追問:答案完整嗎?等號是否取到? 圖4 生21:如圖4,當-k=1時,在邊AD上均取到最大值;當-k=-1時,在邊CD上均取到最大值;所以等號成立,所以滿足-1≤k≤1的所有k均可以. 師:從研究等號是否成立這個問題中,同學們還發現了什么結論及注意事項? 生22:①當k=±1時目標函數的最優解不唯一;②斜率對最優解的影響. 生23:同學18提出的目標函數z=x+3y中y的系數為3,而同學19提出的目標函數中y的系數為1,這不具有一般性,能推廣到一般性嗎? 師生同解惑:推廣到一般的目標函數z=ax+by,對b進行討論: 師:在推廣到一般性時,我們又發現了什么需要注意的地方? 生24:圖解法求目標函數最值要關注z的幾何意義(z與縱截距的相關性):若z隨截距的增加而增加,稱z與截距成正相關;若z隨截距的增加而減小,稱z與截距成負相關. 設計意圖:通過讓學生自編目標函數,激發學生學習興趣,提高學生主動探索的能力,并引導學生探究出以下幾點結論: ①在哪里取到最優解有兩種思路:可以經過平移得出,也可通過比較斜率大小得出;②在可行域的上下頂點能否取到最值與目標函數的斜率有關系;③最優解不一定唯一;④圖解法求目標函數最值要關注z的幾何意義. 4.運用鞏固,內化遷移 師:大家看到這些閥門圖片應該都不陌生,因為家鄉是有名的閥門之都,每個工廠經常會遇到資源利用、人力調配、生產安排等問題,這就用到運籌學,而本節線性規劃正是運籌學最主要的一部分,通過數學建模把實際問題轉化為數學問題來求解,所以線性規劃是溝通代數與幾何的橋梁,集數與形于一身,下面我們來看具體實例: 例1 某工廠用A、B兩種配件生產甲、乙兩種產品,每生產一件甲產品使用4個A配件耗時1h,每生產一件乙產品使用4個B配件耗時2h,該廠每天最多從配件廠獲得16個A配件和12個B配件,生產一件甲產品獲利2萬元,生產一件乙產品獲利3萬元,按每天工作8h計算,采用哪種日生產安排利潤最大? 師:面對繁雜冗長的應用題,該如何處理相關信息? 生25:列表: 所需材料產品類型 A配件(≤16)B配件(≤12)耗時t(≤8)甲401乙042 圖5 解:設甲、乙兩種產品分別日生產x,y件,利潤為z,則z=2x+3y,且約束條件為 點評:這里要注意可行域是由整點組成的一個區域,可行域內的所有整點即為所有可行的日生產安排.在可行解為整點且個數比較少時求最值及最優解有無更簡潔的方法? 生26:可以直接選擇相對較大的(x,y)代入嘗試即可得出最值及最優解. 師:請歸納一下圖解法求解線性規劃實際應用問題的一般步驟. 生27:①根據已知條件寫出線性約束條件及目標函數;②畫出可行域;③平移目標函數找出與可行域有公共點且縱截距最大、最小的直線;④根據平移結論求出最優解;⑤作出答案(還原成實際問題). 簡化為:寫、畫、移、求、答. 設計意圖:對如何求解線性規劃問題本節課從課后閱讀與思考出發進行了研討,成功突破一個重難點,而實際應用問題也是本節的一個重難點,這就需要建立數學模型將復雜的實際問題轉化為易于理解和操作的數學問題,再利用線性規劃求解,使學生在具體情境中感受并由此產生用數學知識解決實際生活中問題的愿望,體會不等式是解決實際問題的重要數學模型和有效工具,形成良好的思維方式,進一步明確數學問題源于生活并可用于生活,學好數學的目的在于應用. 5.回顧反思,拓展問題 請總結一下我們這節課學到了哪些知識(構建知識框架)? 課后作業:教材P91:練習1,2; 練習3 已知函數f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范圍; 練習4 設等差數列{an}的前n項和為Sn,若S4≥10,S5≤15,求a4的最大值. 設計意圖:通過課本練習1鞏固圖解法求解線性規劃的一般步驟,并再次理解最優解不一定在上下頂點取到,以及目標函數z的幾何意義;通過課本練習2促使學生面對實際應用問題該如何處理,明白數學源于生活,也應用于生活;另外補充了兩道練習,學生猛一看是前面知識內容,自然而然會用前面知識求解,這兩道練習的目的是激發學生創設觀察、比較、歸納、探究老題新做,促使學生用線性規劃去求解,發現一題多解,多題歸一;另一方面提示學生在學習中要學會新舊知識之間的融匯貫通,及時去歸納總結,反思提升,建立起新舊知識間的橋梁. “數據分析、數學建模”是高中數學六大核心素養的一部分.如何使該核心素養落實到教學實處?本課采用問題導學的方式激發學生的認知結構,建立新舊知識間的聯系,促使學生從數、形兩方面學會數據分析,推理錯誤原因.利用問題串來調控教學,鼓勵學生發現問題,質疑探索,拓展問題,培養學生的問題意識、反思意識.通過解決問題、自編題目、推廣問題、歸納總結等靈活的教學手段,發展學生認識數學知識背后的一些通性通法,提高學生的邏輯思維能力;并引導學生面對繁雜冗長的實際應用問題,能夠建立相應的數學模型進行求解;通過課堂小結驅動學生建構起本節內容的知識框架;以及通過課下作業促使學生發現新舊知識間的聯系,提升學生歸納總結、一題多解、多題歸一的能力.因此設計有效的課堂教學內容,創設導學功能強的問題,激發學生深入探索知識間的聯系和數學思想,探索數學學習的基本方法和步驟,達到對數學知識和概念的深入理解,是落實數學核心素養目標的基本途徑,也是核心素養下數學課堂教學追求的高度.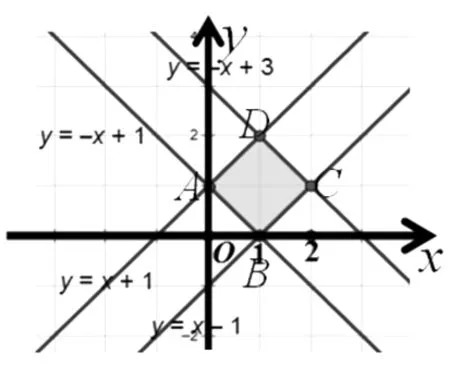
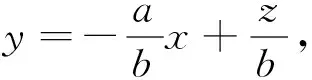
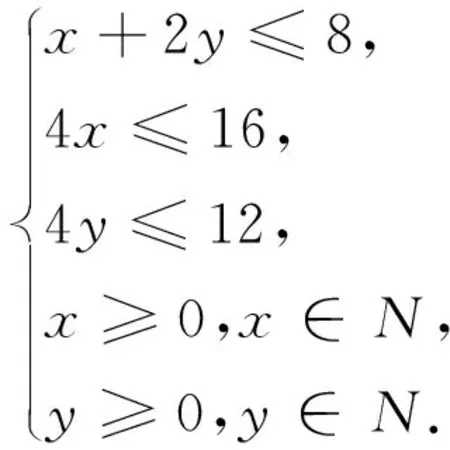
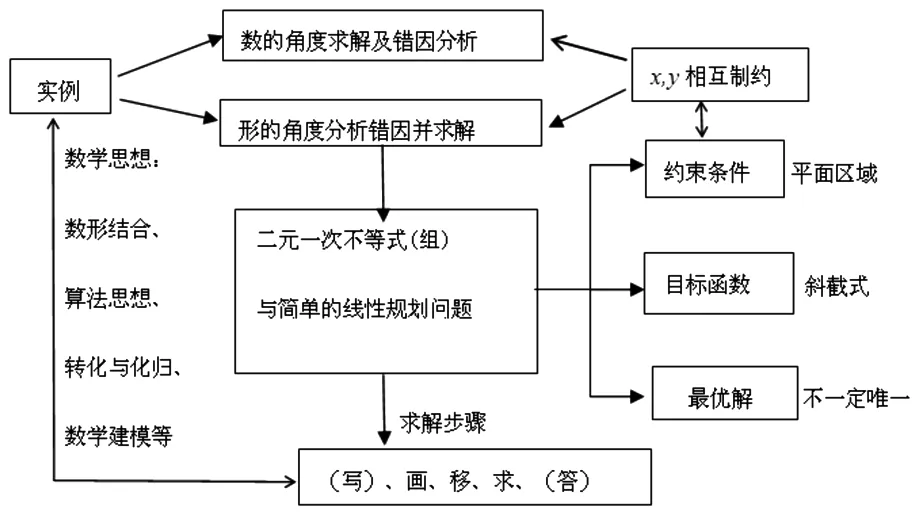
三、教后反思

