逐層探究 提升素養
——以圓錐曲線中的一個定值問題為例

北京師范大學鹽城附屬學校 (224007) 郝文華

(1)求橢圓E的方程；

(2)經過點P(-2,0)分別作斜率為k1,k2的兩條直線分別與橢圓E交于M,N兩點，當M,N兩點關于y軸對稱時，求k1·k2的值.

針對上敘解答過程,作如下探究.

探究1：能否“設而不求”？

探究2：能否推廣到橢圓的一般情形？

探究3：換成右頂點呢？

此時，又有同學提出，能否換成上下頂點呢？此問題剛一提出，很快就有同學發現，若將點P換成上下頂點，兩條直線的傾斜角互補，因此k1·k2非定值.接著，又有學生提出如下問題：

探究4：若點P換成上下頂點，將條件“M,N兩點關于y軸對稱”變為“M,N兩點關于x軸對稱”，k1·k2是否為定值呢？

學生稍有成就感！并進一步提出，以上幾種情況均為M,N兩點關于坐標軸對稱，若點P為橢圓左頂點，M,N兩點關于原點成中心對稱呢？

探究5：若點P為左頂點，將條件“M,N兩點關于y軸對稱”變為“M,N兩點關于原點對稱”，k1·k2是否為定值呢？

學生很驚喜，繼而發現，此問題中的點P完全可以換成橢圓的其他三個頂點！

教師接著進一步提出：

探究7：能否推廣到圓？

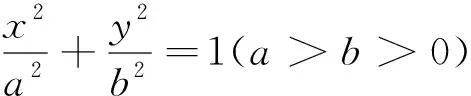
這種探究過程留給同學們課后繼續進行，從中可以使同學們深切感受到圓錐曲線中定值問題的博大與精深.

2017年版課標明確指出，“數學學科核心素養是數學課程目標的集中體現，是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現，是在數學學習和應用過程中逐步形成和發展的.”因此，核心素養的提升，重在日常教學過程，貴在對數學問題本質的探究與延伸、解決方法的多樣化選擇.這對學生關鍵能力的培養是關鍵的，必備品格的養成是必備的.在數學教學與試題講解中，會遇到很多類似的教學片段，如果我們只是就題論題，一味地追求試題本身的解答，忽視解題后的再思考，就會錯過提高的機會.相反，對于一些內涵豐富，思維性較強的數學問題，教師如果能抓住時機，巧妙地加以設計、引導，不惜時間，適當挖掘，于細微處大膽放開，破除試題講解中的“一言堂”現象，并以“師生交流、共同探究”的教學模式取而代之，必將使師生共同提升，真正實現學生的解題思維水平的提高與解放，進而將核心素養的提升落到實處.