判別式巧解一類最值問題例析

新疆烏魯木齊市實驗學校 (830026) 符強如

引例若正實數m,n滿足m+2n=3mn，求m+n的最小值

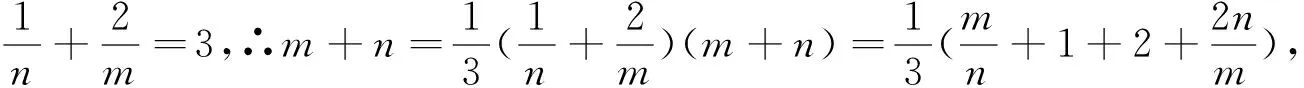
評注:引例的解法多樣，有的簡潔，有的繁瑣，但對一般學生而言都需要較強的技巧.我們可從學生最熟悉的二次方程的判別式來解決.

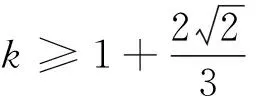
評注:判別式法是由等量關系得到不等關系的一個重要方法.若給定關于x、y的一個二次式，去求解另一個代數式的值或范圍，可令所求式子等于k，消去一個變量x(y)，得到一個關于y(x)的一元二次方程，根據題意其判別式大于等于零，即轉換成關于k的不等式，求解出k的值(范圍)即為所求值(范圍)，此方法可稱為k值代換法，其本質就是“Δ判斷法”，即判別式法.

例1 若實數x,y滿足x2+y2+xy=1，求x+y的最大值.

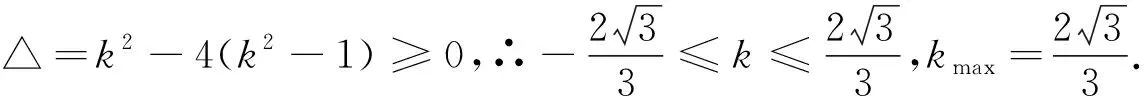
例2 已知實數a,b,c滿足a+b+c=0，a2+b2+c2=1，求a的最大值.

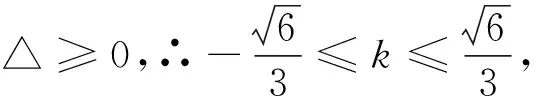
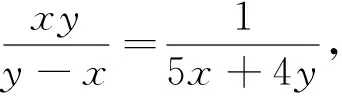
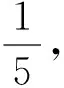
通過以上例題我們不難發(fā)現，通過二次方程的判別式方法來巧解這一類雙變量的最值問題，能簡化推理和運算過程，具有簡捷、易想、明快的特點，彰顯了化歸與轉化的思想在解題中的威力.