基于一類廣義三階KdV方程的精確解探討
李奇芳
(山西財(cái)貿(mào)職業(yè)技術(shù)學(xué)院 山西 太原 030031)
1 研究背景
在自然科學(xué)和工程技術(shù)里,不少現(xiàn)象不能采用線性模型描述,如大幅度擺動(dòng),自激震蕩,電路的機(jī)理等.所以,近年來(lái),對(duì)非線性問(wèn)題的研究在物理,化學(xué),生物,數(shù)學(xué)等領(lǐng)域得到了廣泛而深入的開(kāi)展,特別是尋找非線性方程的精確解受到廣泛關(guān)注.由于非線性現(xiàn)象與非線性偏微分方程有著密切的聯(lián)系,非線性偏微分方程的精確解在許多的科技領(lǐng)域發(fā)揮著重要作用,因此,為了更好的理解自然界中眾多的非線性現(xiàn)象的機(jī)制,必須知道與這些非線性現(xiàn)象相符的非線性偏微分方程的精確解。郭婷婷等人(2017)提出運(yùn)用雙Bell多項(xiàng)式確定KdV方程的雙線性,并求得其遞推公式[1]。郭峰等人(2018)提出利用平均值離散梯度的模式驗(yàn)證KdV方程組能量守恒理論的正確性[2]。趙露等人(2018)通過(guò)簡(jiǎn)化的雙典型方法測(cè)試雙模KdV方程中的線性及非線性參數(shù),從而得到精確解[3]。基于此,可以看出,利用KdV方程算法求解非線性模型,并用這種方法求解CH-DP方程更加簡(jiǎn)潔明了。
2 KdV方程的概述
2.1 研究方向

2.2 研究方法
對(duì)于一個(gè)關(guān)于獨(dú)立變量的一類非線性偏微分方程如(1)所示:
H1(u,ux,ut,uxx,uxt,utt,…)=0.
(1)
該方法通過(guò)下面四個(gè)步驟尋找非線性偏微分方程的精確解,如方程(2)所示:
u(x,t)=φ(x,t)+R,
(2)
其中R任意常數(shù),將變換(1)代入(2)中,則公式1轉(zhuǎn)換為下面的形式,如方程(3)所示:
H2(φ,φx,φt,φtt,φxt,φtt…)=0.
(3)
而后確定常數(shù)R的值.如方程(4)所示:
Φ=φ-α2φxx
(4)
其中α≠0,將方程(3)代入方程(4)使方程(4)的各項(xiàng)表達(dá)式都包含Φ或者Φ的各階導(dǎo)數(shù),根據(jù)方程各項(xiàng)之間系數(shù)的關(guān)系,得出R的取值。
(三)例題模擬
例如:考慮如下DGH方程,如方程(5)所示:
ut+2kux+3uux-(uxxt+uuxx+2uxuxx+γuxx=0,
(5)
其中k,γ是任意常數(shù).將公式(2)代入方程(5),如方程(6)所示:
φt+(2k+3R)φx+3φφx-φxx-φφxxx-2φxφxx+(γ-R)φxxx=0.
(6)
方程(6)可變?yōu)槿绶匠?7)所示:
(φ-φxx)t+2φx(φ-φxx)+φ(φ-φxx)x=-(2k+3R)φx-(γ-R)φxxx·
(7)
由方程(4),取α2=1得如方程(8)所示:
Φt+2φxΦ+φΦx=-(2k+3R)φx-(γ-R)φxxx·
(8)
為了使方程(8)的每一項(xiàng)都包含Φ或者Φ的各階導(dǎo)數(shù),如方程(9)所示:
-(2k+3R)=γ-R,
(9)
化簡(jiǎn)可得如方程(10)所示:
(10)
將方程(10)代入方程(8)得如方程(11)所示:
(11)
顯然,Φ=0是方程(11)的解.
求方程Φ=0的解.注意到Φ=φ-α2φxx=0是線性微分方程,因此容易得到該方程的更一般形式的解.獲得方程(1)的精確解。通過(guò)方程(4)的變形,方程(11)的每一項(xiàng)都包含Φ或者Φ的各階導(dǎo)數(shù),則當(dāng)φ(x,t)是方程Φ=0的解時(shí),φ(x,t)也是方程(3)的解.實(shí)際上,在方程(11)中,當(dāng)φ(x,t)是方程Φ=0的解時(shí),φ(x,t)也是方程(11)的解.通過(guò)改變常數(shù)t的取值來(lái)擴(kuò)展方程Φ=0的基礎(chǔ)解,從而得到方程(1)的一系列的精確解.
3 一類廣義三階KdV方程的求解
3.1 一類廣義三階KdV方程的精確解
在這部分,將應(yīng)用這種簡(jiǎn)單的方法得到廣義三階KdV方程的不同解.廣義三階KdV方程如方程(12)所示:
(12)
其中α,β,ν為任意常數(shù).
令u(x,t)=φ(x,t)+R,將其代入方程(12)后如方程(13)所示:
(13)
根據(jù)研究方法,方程(13)可轉(zhuǎn)換如方程(14)所示:
(14)
令Φ=φ+νφxx,為了使方程(14)的每一項(xiàng)包含Φ或者Φ的各階導(dǎo)數(shù),如方程(15)所示:
(15)
化簡(jiǎn)可得如方程(16)所示:
(16)
因此方程(14)可以寫為如方程(17)所示:
(17)
注意到Φ=φ+νφxx,所以,方程(17)可以變?yōu)槿绶匠?18)所示:
(18)
3.2 情景分析
我們需考慮方程(19)的解:
φ+νφxx=0.
(19)
情形假設(shè)φ<0.
容易求出方程(19)的基本解組如方程(20)所示:

(20)
其中A(t),B(t)是任意可微函數(shù). 是方程(19)的解,易知如方程(21)、公式(22)所示:

(21)
和

(22)
由方程(23)、方程(24)所示:

(23)
和
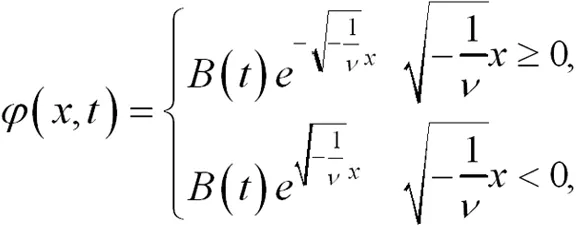
(24)
可得如方程(25)、方程(26)也是方程(19)的解:
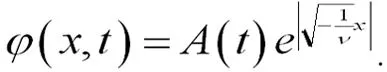
(25)

(26)
所以,當(dāng)如方程(27)所示時(shí),也是方程(19)的解.

(27)
由于A(t),B(t)是任意可微函數(shù),則可以擴(kuò)展解方程(21)后,如方程(28)所示:

(28)
其中c1,c2為任意常數(shù).
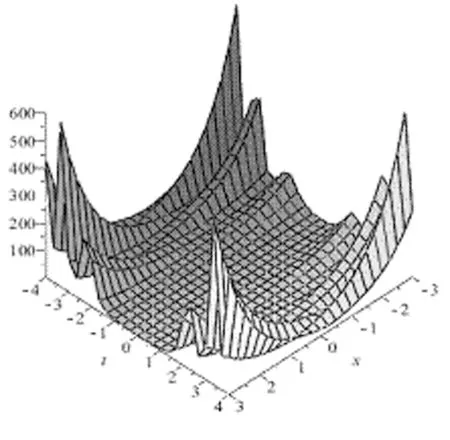
不妨假設(shè)0 (29) 所以可得如方程(30)所示也是方程(19)的解. (30) 此外,還能擴(kuò)展方程(21)如方程(31)所示: (31) 其p(t),q(t)中為任意函數(shù),通過(guò)檢驗(yàn),也是方程(19)的解. 類似地,對(duì)任意的x構(gòu)造,如方程(32)所示: (32) 所以方程(32)也是方程(19)的解. (32) (33) (34) 也是方程(19)的解.其中Ai(t),Bj(t),pi(t),qj(t)是任意可微函數(shù),i=1,2,…N,j=1,2,…M,N,M是任意正整數(shù)。類似可得如方程(35)、方程(36)也是方程(19)的解[5]. (35) (36) 根據(jù)雙曲函數(shù)的定義,可知方程(37)、方程(38)也是方程(19)的解. (37) (38) 情形ν>0. 容易求出方程(19)的基本解組為如方程(39)、方程(40)所示: (39) 其中c(t)為任意可微函數(shù)[6]。 (40) 值得注意的是,從上面的這些構(gòu)造過(guò)程中,可以得到方程(19)的其他精確解,由于篇幅所限,在這里給予省略. 故方程(13)有下列解,如方程(41)-方程(50)所示: (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) 根據(jù)所求的精確解,利用Maple軟件將方程(41)-(45)及(50)的解的波形圖繪制如下: 繪圖時(shí),方程(41)、方程(42)、方程(44)都取ν=-1,α=-1,β=1,N=1,M=1,方程(50)取ν=3,α=1,β=3,N=1,M=1.如圖1-4所示: 圖1(a)是當(dāng)A(t)=log10t,B(t)=sint,x[-20,20],t[1,10]時(shí),方程(41)的波形圖. (b)是當(dāng)A(t)=sin,B(t)=cost,x[-30,30],t[-15,15]時(shí),方程(41)的波形圖. (c)是當(dāng)A(t)=sinht,B(t)=tant,p(t)=sint,q(t)=sint,x[-40,40],t[-1,1]時(shí),方程(42)的波形圖. (d)是當(dāng)A(t)=sinht,B(t)=cost,p(t)=sint2,q(t)=sint3,x[-2,2],t[-8,8]時(shí),方程(42)的波形圖. (e)是當(dāng)A(t)=t2,B(t)=t,p(t)=sint2,q(t)=cost3,x[-3,3],t[-4,4]時(shí),方程(44)的波形圖. (d)是當(dāng)A(t)=et2,B(t)=cost,p(t)=sint2,q(t)=cost3,x[-10,40],t[-1,1]時(shí),方程(44)的波形圖. (g)是當(dāng)C(t)=log10t,x[-20,20],t[0.1,10]時(shí),方程(50)的波形圖. (h)是當(dāng)C(t)=sin10t,x[3.5,11],t[-13,13]時(shí),方程(50)的波形圖. 求解非線性偏微分方程的精確解是一種簡(jiǎn)單方法,這種方法對(duì)于求解非線性偏微分方程是有效和直接的,它可以避免乏味的重復(fù)計(jì)算。這種方法之所以簡(jiǎn)單關(guān)鍵在將原方程進(jìn)行轉(zhuǎn)化,轉(zhuǎn)化為多個(gè)簡(jiǎn)單的常系數(shù)高階常微分方程,最終只需求出簡(jiǎn)單的常系數(shù)高階常微分方程的解。便可得出原方程的解。本文以廣義三階KdV方程為例,用簡(jiǎn)單方法求出了它的許多精確解,并且借助數(shù)學(xué)軟件MAPLE,在一定參數(shù)條件下得到了該方程的一些特殊解的波形圖。

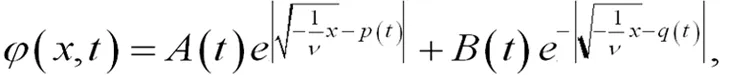
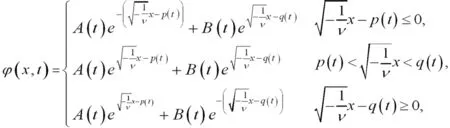






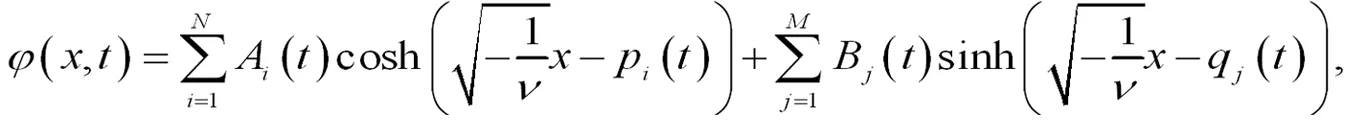



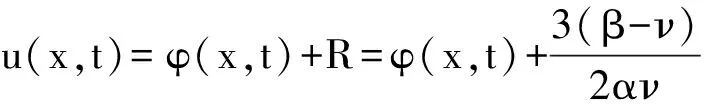




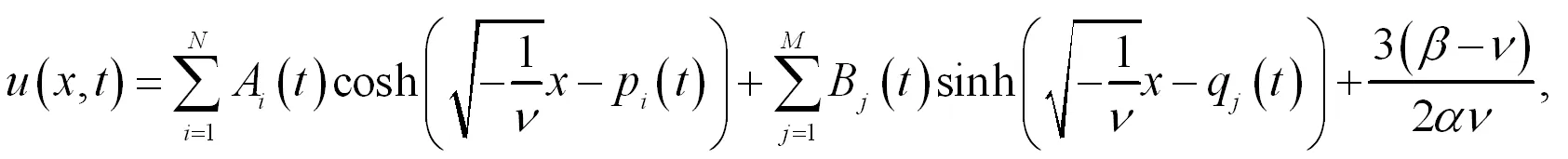




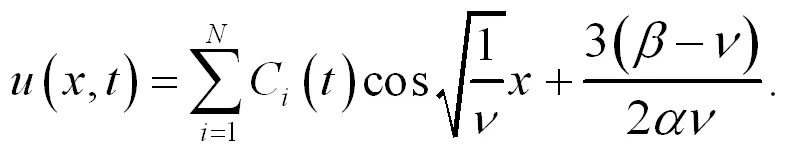
(三)精確解的波形圖



四、結(jié)論
 呼倫貝爾學(xué)院學(xué)報(bào)2020年2期
呼倫貝爾學(xué)院學(xué)報(bào)2020年2期
- 呼倫貝爾學(xué)院學(xué)報(bào)的其它文章
- 現(xiàn)代漢語(yǔ)課程教學(xué)過(guò)程中教師的問(wèn)題引領(lǐng)
- “OBE”理念下混合式教學(xué)方法改革與實(shí)踐
——以河北民族師范學(xué)院《工筆花鳥(niǎo)》課程為例 - 校園心理劇在學(xué)校心理健康教育中的應(yīng)用分析
- 優(yōu)秀傳統(tǒng)文化融入幼兒園師德教育的探索
- 疫情對(duì)民族地區(qū)大學(xué)生就業(yè)創(chuàng)業(yè)的影響及對(duì)策研究
- 推動(dòng)鄉(xiāng)風(fēng)文明建設(shè)路徑研究
——基于“功德銀行”積分視角
