可重復(fù)使用飛行器再入姿態(tài)的區(qū)間二型自適應(yīng)模糊滑模控制設(shè)計

楊珍書，毛奇，竇立謙

（1.江蘇航空職業(yè)技術(shù)學(xué)院 航空工程學(xué)院 鎮(zhèn)江市無人機應(yīng)用創(chuàng)新重點實驗室，鎮(zhèn)江212134；2.天津大學(xué) 電氣自動化與信息工程學(xué)院，天津300072）

為進一步推動空間應(yīng)用的深入和空間技術(shù)的發(fā)展，可重復(fù)使用飛行器（Reusable Launch Vehicle，RLV）受到了廣泛的關(guān)注與研究。作為一類新型的天地往返飛行器，RLV兼具航空器與航天器特點，其在軍事和民用領(lǐng)域具有廣泛的應(yīng)用前景［1-2］。作為一類多變量系統(tǒng)，RLV具有較強的非線性和強耦合性，且在再入返回過程中易受飛行環(huán)境和飛行范圍的影響，由此對可重復(fù)運載器控制系統(tǒng)設(shè)計產(chǎn)生了極大的挑戰(zhàn)［3-4］。

為了保證RLV安全且可靠的再入飛行，國內(nèi)外學(xué)者在近年來進行了非常多的研究工作。Groves等［5］基于飛行器的線性化模型，設(shè)計了線性二次型調(diào)節(jié)器控制方法。但由于飛行器模型具有較大的非線性，線性化后的模型與飛行器自身模型存在一定的建模誤差。Georgie和Valasek［6］針對再入飛行器提出了非線性動態(tài)逆姿態(tài)控制策略。然而，當(dāng)模型存在較大不確定時，此控制策略不能實現(xiàn)非線性項的對消，進而影響飛行器控制性能。Fiorentini等［7］利用反步方法思想針對飛行器設(shè)計了非線性魯棒控制器，但在計算過程中，由于虛擬控制指令被多次求導(dǎo)，易產(chǎn)生微分膨脹問題，從而無法保證飛行器跟蹤性能。文獻［8-10］針對飛行器模型特點，利用魯棒自適應(yīng)控制技術(shù)分別設(shè)計了控制器，取得了較好的控制效果。

然而，由于RLV在再入飛行階段動力學(xué)參數(shù)變化較大，易受到模型參數(shù)不確定性和外界干擾的影響，同時飛行器再入模型在轉(zhuǎn)化過程中存在未建模動態(tài)項，因此所設(shè)計的再入RLV控制策略要具有較強魯棒性。滑模控制（Sliding Mode Control，SMC）方法是一類具有較強魯棒性的控制方法，常用于飛行器控制策略的構(gòu)建。Shtessel等［11-12］針對RLV，基于內(nèi)外雙環(huán)結(jié)構(gòu)提出了滑模控制器，進而避免了對姿態(tài)角誤差的高階求導(dǎo)問題。Liu等［13］結(jié)合狀態(tài)擴張觀測器設(shè)計滑模控制策略，取得了良好的跟蹤性能。模糊邏輯系統(tǒng)（Fuzzy Logic System，F(xiàn)LS）由于能較好地處理模型不確定性和非線性項問題，因此受到了眾多學(xué)者關(guān)注［14-17］。相比于type-1模糊系統(tǒng)，type-2模糊系統(tǒng)能在Mamdani和Takagi-Sugeno FLS中提供額外的自由度［18-21］，尤其是在系統(tǒng)存在大量不確定性的情況下能夠提供更好的跟蹤逼近性能。Tao等［22］針對飛行器存在測量噪聲問題，利用type-2模糊系統(tǒng)設(shè)計控制器，使得系統(tǒng)具有較好的跟蹤控制性能。

對此，本文考慮RLV在參數(shù)不確定性和外界干擾影響下系統(tǒng)姿態(tài)跟蹤問題，結(jié)合區(qū)間二型自適應(yīng)模糊系統(tǒng)和滑模控制技術(shù)設(shè)計RLV再入姿態(tài)跟蹤控制策略。首先，基于RLV再入動態(tài)模型和反步策略，將飛行器姿態(tài)模型分為內(nèi)外環(huán)子系統(tǒng)。接著，將RLV再入動態(tài)模型的參數(shù)不確定性和外界干擾分別看作內(nèi)外環(huán)子系統(tǒng)非線性項的一部分。然后，設(shè)計合適的區(qū)間二型模糊系統(tǒng)用于子系統(tǒng)非線性項的估計。同時，利用滑模控制策略和自適應(yīng)技術(shù)構(gòu)造飛行器的外環(huán)子系統(tǒng)的虛擬控制量，進而確定內(nèi)環(huán)子系統(tǒng)的控制律。在姿態(tài)角控制策略設(shè)計中，引入一階低通濾波器以處理虛擬控制量。基于Lyapunov方法在理論上證明閉環(huán)控制系統(tǒng)的穩(wěn)定性，且RLV姿態(tài)跟蹤誤差能收斂在原點附近的小鄰域中。最后，通過RLV六自由度模型的數(shù)值仿真驗證了本文所提出控制方法的有效性及跟蹤性能。

1 問題描述

1.1 RLV再入動態(tài)模型

RLV再入飛行動態(tài)過程可由三自由度質(zhì)心運動的平動方程與三自由度繞質(zhì)心運動的轉(zhuǎn)動方程完整描述。考慮飛行器在再入過程為無動力飛行（總是正確的），RLV姿態(tài)運動方程可以描述為

式中：α為飛行器的迎角；β為側(cè)滑角；μ為傾側(cè)角；p為滾轉(zhuǎn)角速率；q為俯仰角速率；r為偏航角速率；ˉL為滾轉(zhuǎn)通道控制力矩；ˉM為俯仰通道控制力矩；ˉN為偏航通道控制力矩；γ為航跡角；m為飛行器質(zhì)量；v為飛行速度；L為氣動升力；Y為側(cè)向力；Ixx、Iyy、Izz、Ixz為飛行器的轉(zhuǎn)動慣量；g為重力加速度。

注1 本文RLV再入動態(tài)模型是基于如下假設(shè)［1，16］建立的：

假設(shè)1 在再入飛行階段，地球自轉(zhuǎn)速率對飛行器的影響可忽略不計。

假設(shè)2 地球大氣層視為靜止的，且其質(zhì)量變化忽略不計。

1.2 姿態(tài)控制模型

RLV再入動態(tài)模型具有多變量耦合、強非線性等特點，使得再入姿態(tài)跟制器的設(shè)計變得復(fù)雜。為便于設(shè)計RLV再入姿態(tài)控制器，將飛行器模型式（1）轉(zhuǎn)化為如下形式姿態(tài)控制模型：

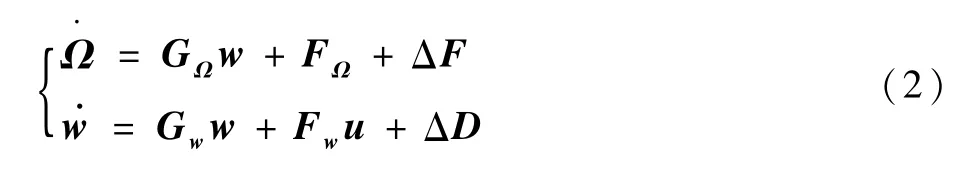
式中：Ω＝［α，β，μ］T為飛行器姿態(tài)角向量；w＝［p，q，r］T為飛行器姿態(tài)角速率向量；u＝［ˉL，ˉM，ˉN］T為控制輸入向量；y＝Ω 為輸出向量；ΔF＝［ΔF1，ΔF2，ΔF3］T為飛行器氣動參數(shù)攝動引起的參數(shù)不確定性項；ΔD＝［ΔD1，ΔD2，ΔD3］T為系統(tǒng)外 界 干 擾 綜 合 項，ΔD ＝I－1（ΔD0－ΔI˙w－MΔIw），I和M 為矩陣（其具體表達式在下文給出），ΔI為參數(shù)不確定性，ΔD0為外界干擾；FΩ＝

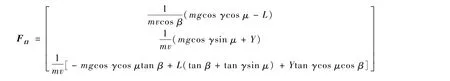
注2 考慮RLV的背景意義和實際飛行情形，假設(shè)3和假設(shè)4總是合理的。在實際再入姿態(tài)控制中，飛行器函數(shù)矩陣的上下界并不需要確定得到。同時，假設(shè)3和假設(shè)4確保了系統(tǒng)函數(shù)矩陣的非奇異性。

本文旨在針對RLV再入動態(tài)模型式（1）和式（2），給定任意滿足假設(shè)3的期望指令信號，設(shè)計合理的再入姿態(tài)控制律，使得RLV能跟蹤期望指令信號，且飛行器閉環(huán)控制系統(tǒng)的穩(wěn)定性及姿態(tài)跟蹤誤差的有界性能得以保證。

2 RLV再入姿態(tài)控制策略

2.1 區(qū)間二型模糊系統(tǒng)

利用單值模糊器、乘積推理機及中心集降階器，可得到區(qū)間一型模糊集輸出，該輸出可由2個端點yl、yr表示。通過計算和的均值，去模糊化區(qū)間集，得到去模糊化的清晰輸出為

2.2 再入姿態(tài)控制器設(shè)計

步驟1 外環(huán)姿態(tài)角控制器。

定義姿態(tài)角跟蹤誤差為eΩ＝Ω－Ωd∈R3×1，其中Ωd＝［αd，βd，μd］T為系統(tǒng)給定姿態(tài)角跟蹤信號，且其導(dǎo)數(shù)Ω·d有界。

由飛行器姿態(tài)控制模型式（2），得到RLV姿態(tài)角跟蹤誤差動態(tài)為

定義姿態(tài)角子系統(tǒng)的滑模面為SΩ＝DΩeΩ＝DΩ（Ω－Ωd），則

步驟2 內(nèi)環(huán)姿態(tài)角速率控制器。

現(xiàn)設(shè)計虛擬控制輸入wd。定義姿態(tài)角速率跟蹤誤差ew＝w－wd∈R3×1，其中wd＝［pd，qd，rd］T為期望姿態(tài)角速率跟蹤信號，且其導(dǎo)數(shù)˙wd有界。

基于飛行器控制模型式（2），姿態(tài)角速率的跟蹤誤差方程可表示為

類似地，定義姿態(tài)角速率子系統(tǒng)滑模面為Sw＝Dwew＝Dw（w－wd），可得滑模面動態(tài)為

3 穩(wěn)定性分析

定理1 對于飛行器控制模型式（2），且滿足假設(shè)3、假設(shè)4和引理1，飛行器姿態(tài)角和姿態(tài)角速率子系統(tǒng)的控制律分別設(shè)計為式（13）和式（26），并選取參數(shù)向量自適應(yīng)更新律分別為式（16）、式（18）和式（28）、式（30），則RLV閉環(huán)控制系統(tǒng)是半全局一致有界穩(wěn)定的，且飛行器姿態(tài)角跟蹤誤差能收斂于原點附近的一個小鄰域內(nèi)。

證明 選取Lyapunov函數(shù)為

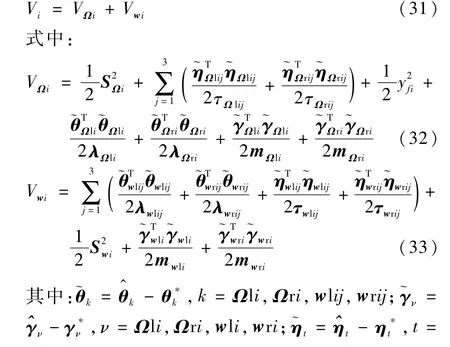
類似地，結(jié)合式（28）、式（30）、式（36）和不等式（38）證明，可以得到即

綜上，整理式（40）和式（41）可得到

式（42），可得

4 仿真驗證

為驗證所提控制策略的有效性，應(yīng)用所提出的控制方法針對RLV再入動態(tài)模型進行仿真實驗。

4.1 參數(shù)設(shè)定

再入飛行器轉(zhuǎn)動慣量值分別設(shè)定為Ixx＝434 270 slug·ft2，，Ixz＝17 880 slug· ft2，Iyy＝961 200 slug·ft2和Izz＝1 131 541 slug·ft2，1 ft＝0.304 8m，1 slug·ft2＝14.593 9 kg·m2。飛行器其他初始條件如表1所示。

仿真中，選取以高斯型隸屬度函數(shù)為主設(shè)計的區(qū)間二型模糊系統(tǒng)。飛行器控制器待設(shè)計參數(shù)分別設(shè)置如下：KΩ1＝diag（1，0.8，1），Kw1＝18I3×3，KΩ2＝diag（1.6，1.4.1.6），Kw2＝15I3×3，Kf＝0.1I3×3；λΩ1＝λΩr＝cΩl＝cΩr＝［1.5，1.2，1.5］T，λwl＝λwr＝cwl＝cwr＝［1，1，1；1，1，1；1，1，1］，δ＝0.001［1，1，1］T；mΩl＝mΩr＝bΩl＝bΩr＝［1，1，1.2］T，mwl＝mwr＝bwl＝bwr＝［1.1，1，0.9］，τΩl＝τΩr＝dΩl＝dΩr＝［1.4，1.4，1.2；1.4，1.4，1.2；1.4，1.4，1.2］，τwl＝τwr＝dwl＝dwr＝［1.2，1.2，1.2；1.2，1.2，1.2；1.2，1.2，1.2］。

表1 再入RLV初始參數(shù)值Tab le 1 Initial param eter values of reentry RLV

此外，為驗證RLV再入姿態(tài)控制器的魯棒性能，針對飛行器控制模型式（2）加入?yún)?shù)不確定性ΔF＝0.1FΩ和外界干擾為

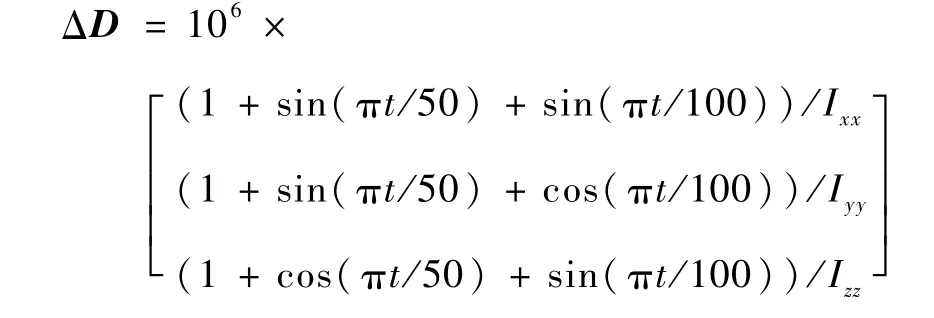
4.2 仿真分析

為了更好地驗證本文所設(shè)計姿態(tài)控制方法的有效性及跟蹤性能，在同樣的條件（模型和初始情況）下與傳統(tǒng)的滑模控制方法進行仿真實驗對比。仿真結(jié)果如圖1～圖4所示。

圖1 姿態(tài)角跟蹤響應(yīng)曲線Fig.1 Attitude angle tracking response curves

圖1為迎角、側(cè)滑角和傾側(cè)角跟蹤曲線。由圖1可以看出，在飛行器模型的參數(shù)不確定性和外界干擾的綜合影響下，所提出的姿態(tài)控制策略能使得再入RLV在很短時間（約2 s）內(nèi)實現(xiàn)對期望指令的穩(wěn)定跟蹤，且其穩(wěn)定跟蹤時間快于傳統(tǒng)滑模控制方法。

圖2為迎角、側(cè)滑角和傾側(cè)角跟蹤誤差變化曲線。圖2表明，所提出的控制策略能夠以更高的精度對期望指令信號進行跟蹤。

圖3為滾轉(zhuǎn)角、俯仰角和偏航角速率變化曲線。由圖3可知，在所設(shè)計控制器作用下，再入飛行器三通道角速率的變化更加平滑。

圖4為飛行器的滾轉(zhuǎn)、俯仰和偏航三通道所需力矩響應(yīng)曲線。由圖4可知，相比于傳統(tǒng)的滑模控制方法，RLV在所提出的姿態(tài)跟蹤策略下能產(chǎn)生更加平滑的控制力矩且無抖振現(xiàn)象。

圖2 姿態(tài)角跟蹤誤差變化曲線Fig.2 Attitude angle tracking error changing curves

圖3 姿態(tài)角速率變化曲線Fig.3 Attitude angular rate changing curves

5 結(jié) 論

本文針對RLV姿態(tài)跟蹤控制問題，考慮RLV再入動態(tài)模型的參數(shù)不確定性和外界干擾情形，基于區(qū)間二型自適應(yīng)模糊技術(shù)提出一種再入姿態(tài)滑模控制策略。

1）該控制策略引入?yún)^(qū)間二型模糊系統(tǒng)對飛行器姿態(tài)角和角速率子系統(tǒng)非線性項進行逼近，有效地解決了RLV再入動態(tài)模型的強非線性問題。

2）結(jié)合滑模控制方法及自適應(yīng)更新律設(shè)計，使得所設(shè)計控制器具有較強的魯棒性。同時，利用Lyapunov方法在理論上嚴(yán)格證明了RLV閉環(huán)控制系統(tǒng)的穩(wěn)定性。

3）通過對飛行器再入模型的仿真對比驗證，所設(shè)計的再入姿態(tài)控制器在RLV再入動態(tài)模型參數(shù)不確定性和外界干擾的影響下，能夠有效地實現(xiàn)對期望指令信號穩(wěn)定且快速地跟蹤，且相比于傳統(tǒng)滑模控制方法具有更好的跟蹤控制性能。

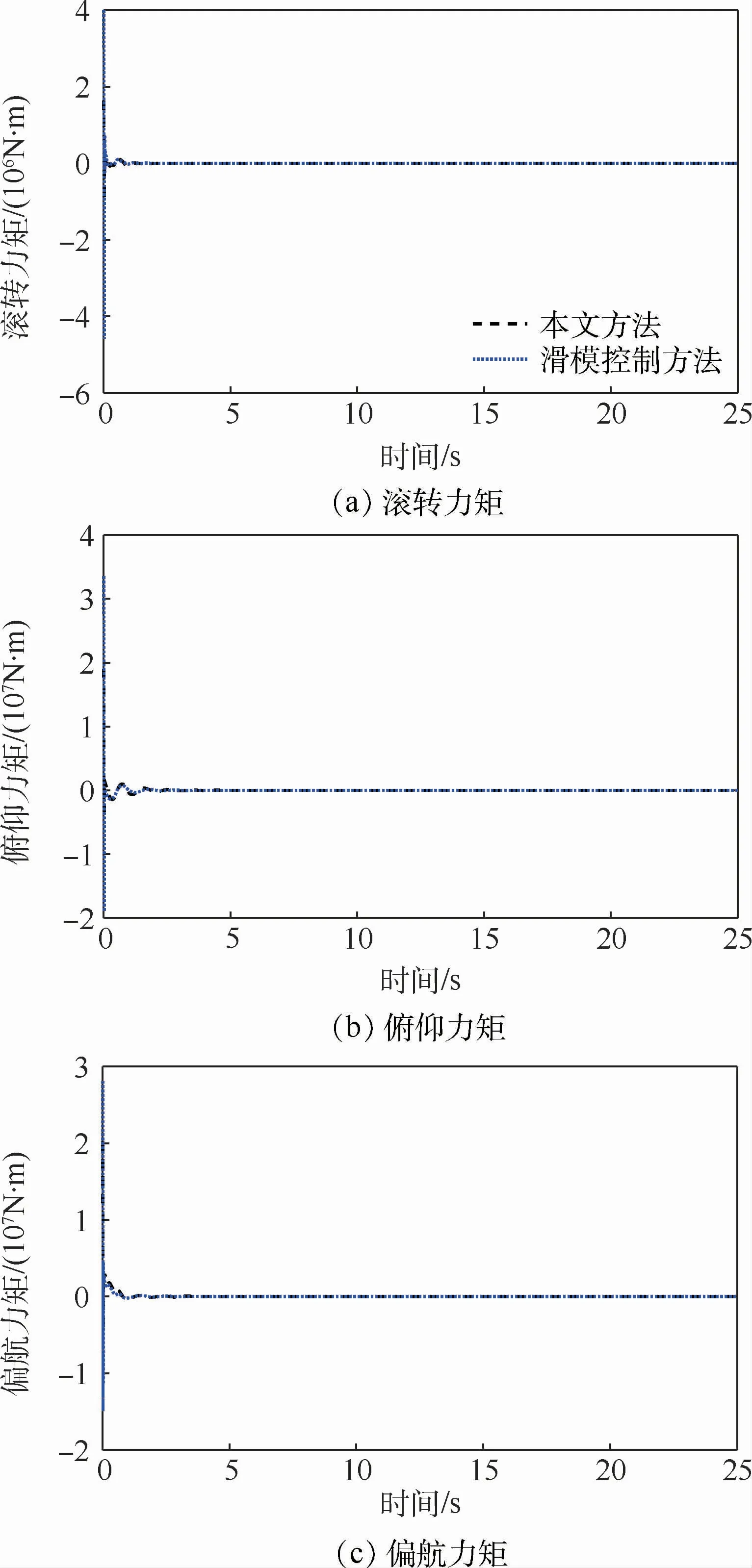
圖4 RLV力矩響應(yīng)曲線Fig.4 Torque response curves of RLV