不確定需求下航空公司樞紐網絡優化設計

樂美龍，鄭文娟，吳明功，王澤坤

（1.南京航空航天大學 民航學院，南京211106； 2.空軍工程大學 空管領航學院，西安710051；3.國家空管防相撞技術重點實驗室，西安710051）

隨著航空管制的放松，各個航空公司都在重建自己的航線網絡，由點對點航線網絡向中樞輻射式航線網絡轉變。中樞輻射式航線網絡通過短途匯運、分運和長途、大容量轉運，使得運輸成本更低，經濟效益更好。但在構建樞紐網絡時，始發地與目的地（OD）需求不確定是困擾航空公司戰略決策的主要原因。研究需求不確定下的樞紐選址與運輸路徑規劃問題能夠幫助航空公司確定最佳的運輸方案以應對季節、市場等因素引起的OD需求波動，使其運營總成本最低。

對樞紐選址問題的設計與優化，O’Kelly［1］、Campbell［2］、Skorin-Kapov［3］、Ernst［4］等 建 立 了 經典的樞紐航線網絡優化模型。之后學者在經典模型的基礎上從樞紐機場容量限制、機場容量多水平決策、OD需求不確定性等角度做了逐步的推進。在樞紐機場容量限制方面，Yang［5］分別考慮樞紐機場總流量限制和樞紐機場中轉流量限制，構建了2個混合整數線性規劃模型，得出了不同容量限制情形下的樞紐選址差異。馮乾等［6］將樞紐選擇和航線設計2個階段綜合考慮，用機場吞吐量衡量機場容量限制，提出了機場容量限制下的多分配樞紐航線網絡設計方法。在機場容量多水平決策方面，Wu等［7-8］將機場容量看作離散變量，確定不同情形下的樞紐位置和路徑流分配，得出不同容量限制情形下的最優網絡。Correia等［9］在機場容量限制的基礎上引入樞紐機場容量多水平決策。Zarei［10］在樞紐機場容量多水平決策的基礎上引入樞紐之間的連接方式差異。Seyed等［11］從容量包絡曲線的角度構建了樞紐機場容量多水平決策的混合整數規劃模型（MILP）。在OD需求不確定性方面，Yang［12-13］和Chiu［13］考慮隨機需求，構建了兩階段的隨機規劃模型，第1階段解決樞紐選址問題，第2階段在第1階段樞紐選擇的基礎上確定不同需求情形下OD之間的路徑和流量分配。Alumur等［14］同時考慮樞紐建設成本的不確定性和OD需求的不確定性，分別構建了單分配、多分配下的優化模型。Qin和Gao［15］、Contreras等［16］研究OD流量不確定情形下樞紐機場無容量限制的樞紐選址問題。胡青蜜和胡志華［17］運用隨機規劃方法研究不確定貨流下的樞紐選址問題。

縱觀國內外研究現狀，對樞紐網絡設計問題從機場容量限制、機場容量多水平決策和OD需求不確定性方面的研究主要存在以下3點不足：①現有研究主要從整個航空運輸市場的角度考慮，但實際規劃航線網絡布局的是航空公司；②現有研究在確定樞紐機場容量時以機場的最大吞吐量作為容量，但是樞紐機場容量受多種因素影響，不同的時期容量可能不同；③現有研究在樞紐容量決策和OD需求不確定性方面獨立研究。研究OD需求不確定性時，未考慮樞紐機場容量多水平決策，在對樞紐機場容量多水平決策研究時未考慮季節、時期等因素造成的OD需求不確定性。

本文從航空公司的角度出發，在機場容量一定的情況下，確定航空公司選擇樞紐機場的最優所占份額。對樞紐機場總容量水平的確定，為了更切合實際，將機場容量看作離港和到港航班的函數，運用歷史統計數據繪制機場容量包絡曲線。同時考慮OD需求的不確定性，構建航空公司樞紐選址問題的多分配、非嚴格的兩階段混合整數隨機規劃模型，并運用實際航空公司數據對模型進行驗證。

1 機場容量包絡曲線

樞紐機場的實際容量與天氣、機場空域構型、跑道構型及數量、停靠的航班類別等多種因素有關。學者通常情況下根據歷史數據將進離港航班之和的最大值表示為單位時間內樞紐機場的容量。對于一個真實的航線網絡，實際容量比理論容量更加精確。單位時間內的機場容量應該表示為到港和離港航班數量的函數，而不是一個常數。這些函數是對歷史數據形成的全部觀測值的包絡，從而構成了機場容量包絡曲線。

機場容量包絡曲線根據一段時間內（1 h）的到達和離開的實際航班數量進行繪制。橫軸表示到港航班數量，縱軸表示離港航班數量。一般情況下運用統計的方法去除低頻率的觀測值，通過拒絕一定比例的觀測頻率來繪制正確的樞紐機場容量包絡曲線。如圖1（a）所示，曲線1表示基于統計數據觀測到的機場容量包絡曲線；曲線2表示修正后的機場容量包絡曲線。圖1（b）中，y1、y2、y3共同構成了機場容量包絡曲線。

圖1 機場容量包絡曲線案例Fig.1 Example of airport capacity envelope curves

2 模型提出

本文采用有向圖建模。假設網絡中有N個節點，包括始發地、目的地和潛在樞紐。非樞紐節點之間既能中轉也能直達運輸。一個非樞紐節點可以連接多個樞紐點，并且規定兩個非樞紐節點之間最多實現兩次中轉。

從航空公司樞紐選址問題的角度出發，基于機場容量包絡曲線，考慮航空公司在樞紐機場的容量多水平決策，以及OD需求的不確定性，構建兩階段的隨機規劃模型。本文將需求的不確定性表示為隨機變量。第1階段以總的網絡運輸成本最低來確定樞紐的位置，第2階段在第1階段樞紐選址結果的基礎上確定不同需求的運輸路徑和路徑上的流量分配。

2.1 模型參數及變量

2.1.1 模型參數

2.2 兩階段模型

樞紐建設是一個長期且耗資的工程，由季節、時期等因素引起的需求不確定性對樞紐節點的選擇不產生影響。因此第1階段模型中的變量Xtk不受需求不確定性的影響，第2階段變量Zij（ω）、Zikmj（ω）取決于需求的不同情形。Z為目標函數值。

1）第1階段

第2階段模型表示每種情形ω下的路徑決策和流量分配決策。式（4）表示情形ω下所有OD中轉和直達的總成本最小。式（5）確保OD之間的需求必須得到滿足。式（6）～式（8）表示流變量之間的關系。其中式（6）、式（7）表示當節點k被選作樞紐時，流經節點k的運輸應被看作中轉運輸；式（8）表示當節點k、m都是樞紐時，k和m之間的運輸應被看作中轉運輸。式（9）表示當節點k不是樞紐時，經節點k中轉的流量為0。式（10）表示流出節點k的流平衡約束。式（11）表示流入節點k的流平衡約束。式（12）表示容量約束，流經節點k的流量應小于節點k的容量。式（13）～式（15）表示變量域的限制。

針對需求不確定下樞紐選址和運輸路徑規劃問題所構建的模型是一個兩階段模型，需要采用迭代算法求解。假設需求情形ω是離散變量，具有有限種可能的情形，每種情形以一定的概率發生。則兩階段的隨機規劃模型可以被寫為確定的等價規劃（Deterministic Equivalent Programming，DEP），如式（16）～式（29）所示。各式的含義等同于兩階段的隨機規劃模型。

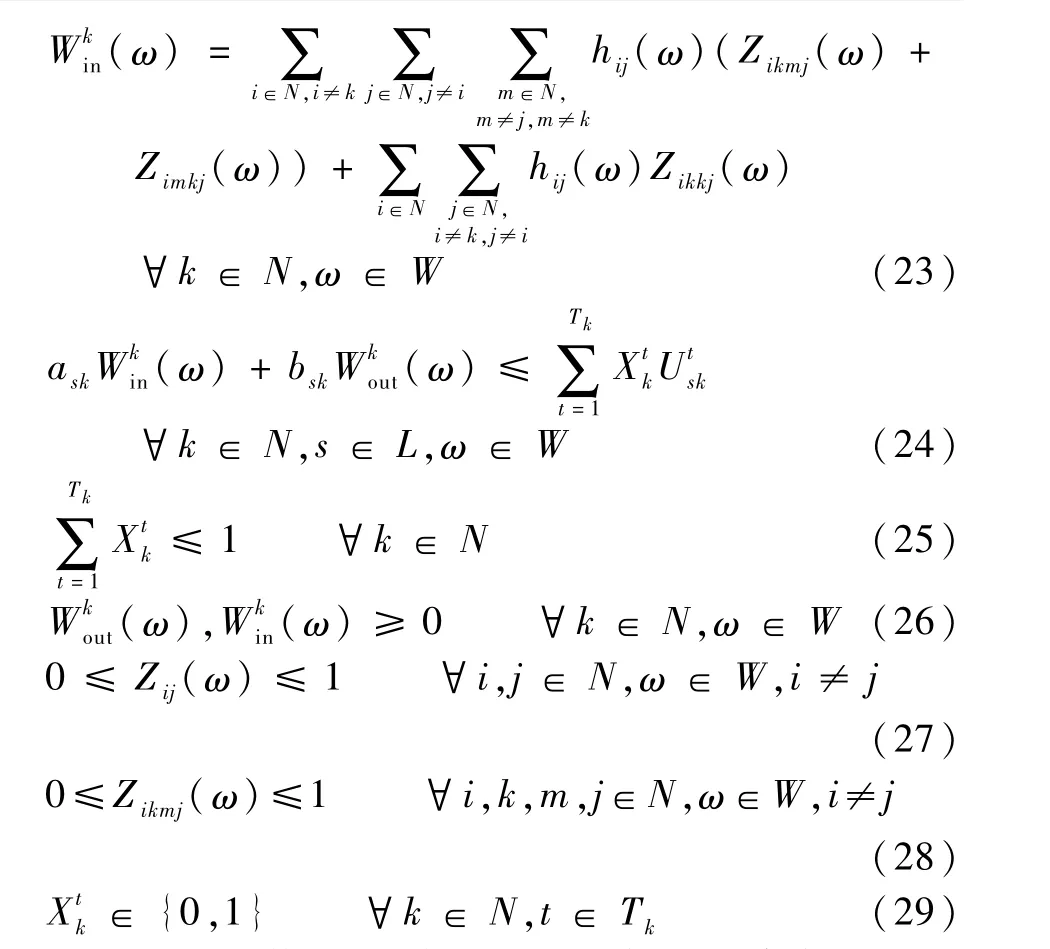
在上述模型中，情形ω下路徑的單位旅客運輸成本表示為

式（30）表明在HS網絡中，對于每種需求情形ω，節點i和j之間的整個運輸成本包括匯運、轉運、分運三部分。由于規模經濟性的存在，隨著路徑流量的增加（h1增加至h4），單位運輸成本逐漸降低，如圖2所示。

圖2 運輸成本的規模經濟函數Fig.2 Scale economy function of transport cost

3 算例分析

3.1 數據輸入

為了驗證模型的有效性，本文以東航為例，選擇13個主要省會機場研究航空公司樞紐網絡設計問題。根據2016、2017兩年的進離港航班數據，統計單位小時內的進離港航班數量如圖3所示（以西安機場為例）。為了獲得機場的年旅客容量，設機場的日開放小時為18 h，每航班的平均旅客數為180，則以旅客數表示的機場容量包絡曲線如圖4所示。

13個機場旅客容量包絡曲線的系數如表1所示。

在13個機場中，任意兩個OD之間的需求，根據2017年實際運力乘以行業航線平均客座率估算。運力數據源于OAG（Official AirlineGuide），客座率數據源于飛常準。東航在某些沒有運力部署的OD上需求設為0。

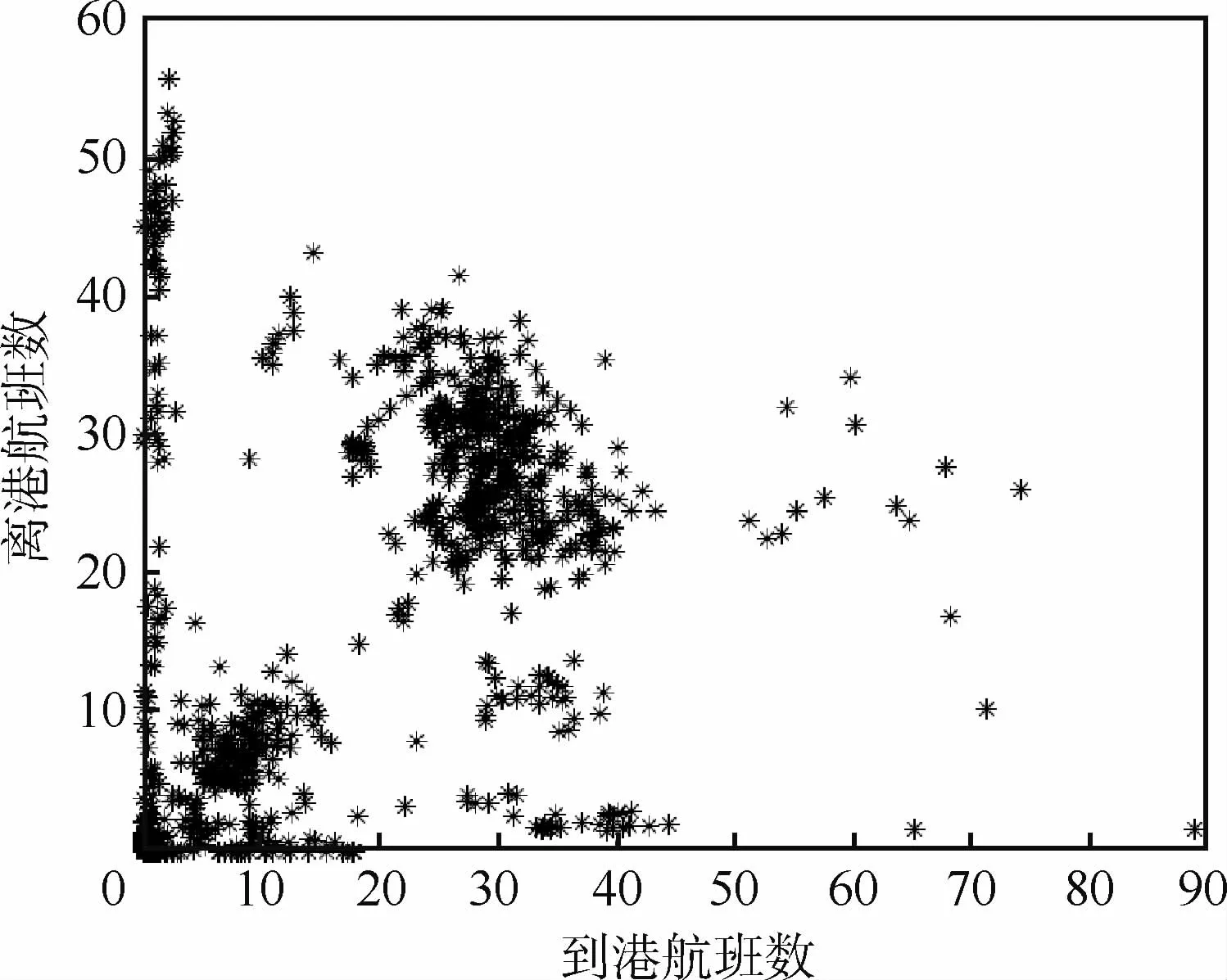
圖3 西安機場單位小時進離港航班數Fig.3 Number of arrival and departure flights per hour at Xi’an Airport

圖4 西安機場旅客容量包絡曲線Fig.4 Envelope curve of passenger capacity of Xi’an Airport

本文對需求不同的考慮，只要根據航空公司的實際做法，即如何應對旺、平、淡季，在文中對應設立了高、中、低3個不同的需求場景。平季需求，即基準需求hij，采用OAG數據計算；高低等級需求按深航博士后創新實踐基地研究，設為1.14hij和0.87hij。根據基地的研究，需求發生的概率由高等級至低等級依次為0.371、0.488和0.141。

根據OAG數據統計得出，東航在任意主協調機場的運力份額不超過20%，因此將航空公司在每個潛在樞紐機場能夠得到的容量情形設置為機場容量包絡曲線最大值的5%、10%、15% 和20%。樞紐機場的建設成本與容量情形有關，用式（31）表示：

式中：ρk為一個常量參數，與機場的規模經濟效應有關。當ρk＞1時表示機場繁忙，航空公司增加在機場的容量份額就得付出更高的單位容量建設成本；當ρk＜1時表示機場不是繁忙機場，增加容量能夠減少樞紐機場的單位容量建設成本。本文定義主協調機場SZX、XIY、URC、CSX、WUH、CTU、PVG、NKG、PEK、KMG為繁忙機場，設ρk＝1.1；其余機場為非繁忙機場，設ρk＝0.9。根據東航2017年公司年報，推斷的樞紐機場建設成本如表2所示。

假設每位旅客的單位運輸成本相同，則任意2個OD之間的運輸成本與航線距離成正比，因此用航線距離來計算其運輸成本。

表1 機場容量包絡曲線系數Tab le 1 Airport capacity envelope curve coefficient

為驗證折扣因子的靈敏度，計算3組不同折扣因子取值下的優化模型，取α＝γ。根據Yang［12］的研究結果，α和γ的范圍為0.7～0.9，β的范圍為0.6～0.8。同時考慮網絡的規模效應，OD需求越大，成本折扣越大。折扣因子的取值見表3。

表2 不同容量情形下的樞紐建設成本Tab le 2 Hub construction cost under different capacity scenarios 107元

表3 不同需求情形下的折扣因子Table 3 Discount factors for different dem and scenarios

3.2 結果展示

運用MATLAB求解DEP模型，得到不同折扣因子情形下的樞紐選址結果如表4所示。

通過對結果中的流變量值進行分析，繪制了不同需求情形、不同折扣因子情形下的航空公司航線網絡，如圖5所示。圖中的黑圓點表示不同折扣因子情形下的樞紐點。

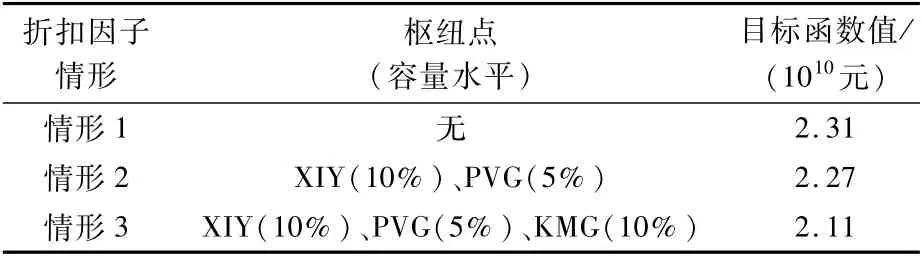
表4 折扣靈敏度下的樞紐選址結果Tab le 4 Resu lts of hub location under discount sensitivity

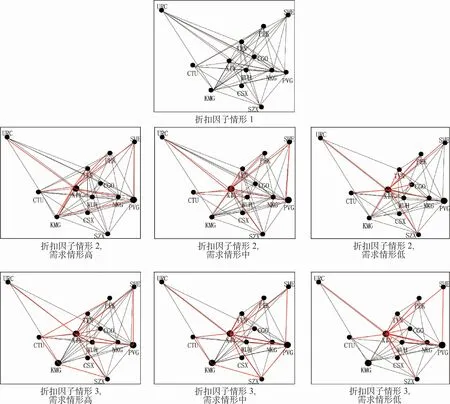
圖5 不同需求和折扣因子情形下的航線網絡布局Fig.5 Route network layout with different demand scenarios and different discount factors

由圖5可以看出，在折扣因子情形1下，由于折扣較小，折扣不足以抵消樞紐的建設成本，模型得出的網絡是完全的點對點網絡，任意2個節點之間直達運輸。在折扣因子情形2下，選擇XIY、PVG作為樞紐，選擇的容量水平分別是10%、5%，網絡中一部分OD直達運輸，一部分OD通過樞紐中轉運輸。不同OD需求情形下的網絡間存在較小的差異，隨著需求的下降，原本直達或通過浦東機場中轉運輸的OD轉向西安中轉，這是因為中轉和直達2種運輸方式的成本存在差異，當受到中轉成本最低的樞紐機場容量限制時，一些OD轉向成本次低的路徑運輸，需求高的時候這種現象更加顯著。在折扣因子情形3下，選擇XIY、PVG、KMG 3個機場作為樞紐，選擇的容量水平分別是10%、5%、10%。隨著OD需求的變化，網絡間的差異與折扣因子情形2下的變化趨勢相同。

表5、表6分別列出了折扣因子情形2和折扣因子情形3下，不同OD需求情形下需要中轉的OD、中轉點和路徑流比例，表中來回運輸路徑相同的城市之間只列一個OD。從表5、表6可以再次看出不同需求情形下OD 的中轉差異。表5中的KMG-SHE、KMG-TYN、SZX-TYN，表6中的WUH-SHE、PVG-URC、CTU-WUH、SZX-NKG都選擇了2條路徑，這是由于目標函數是整個網絡總成本最小，不同容量的樞紐建設成本不同，模型會選擇使得整個網絡總成本最小的樞紐容量，因此這些OD會選擇成本最低的路徑運送一部分流量，剩余流量選擇次低成本的路徑運輸。

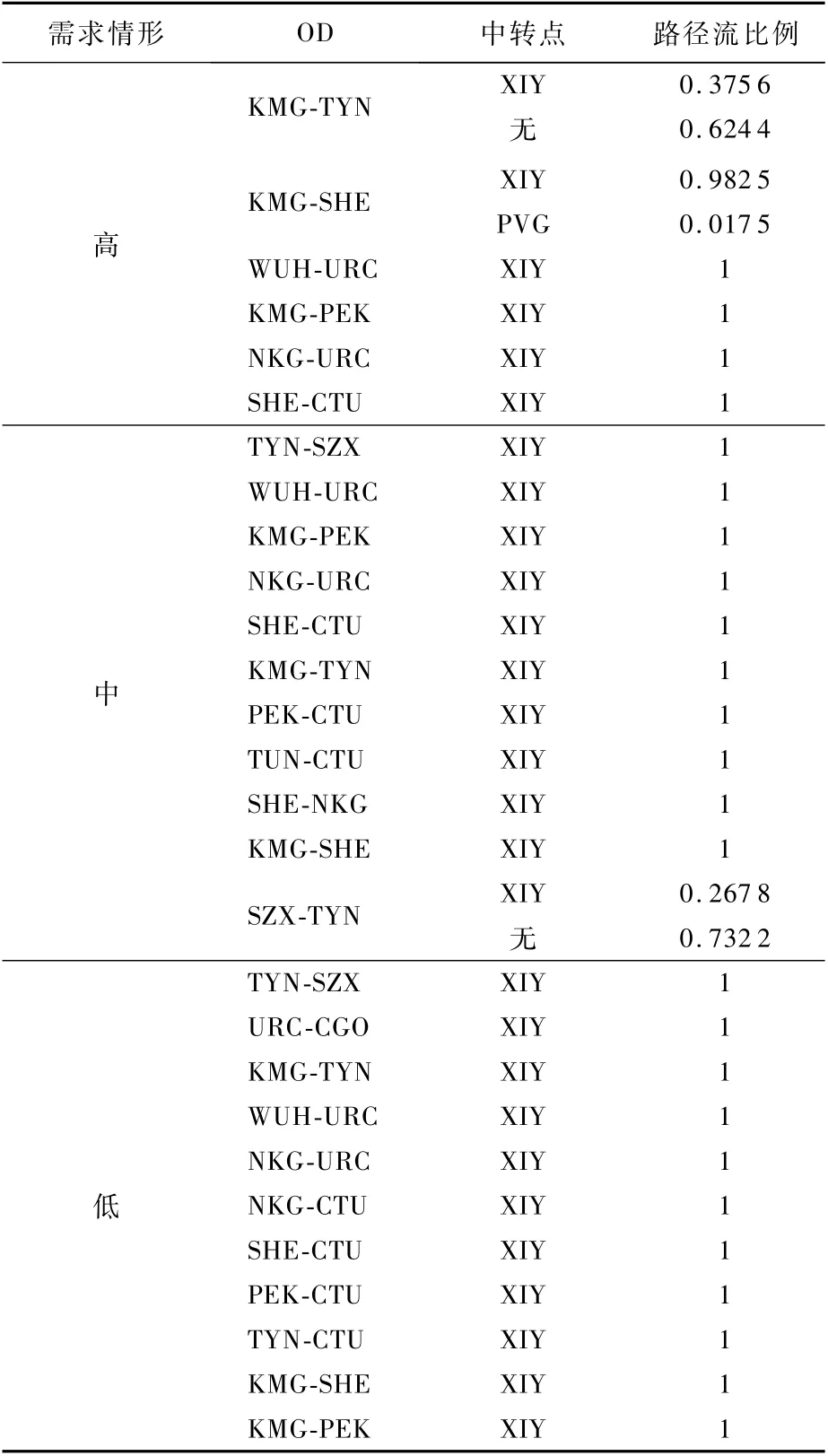
表5 折扣因子情形2下的中轉情況Tab le 5 Transit in discount factor Case 2

表6 折扣因子情形3下的中轉情況Tab le 6 Transit in discoun t factor Case 3

與隨機規劃模型相對應的是傳統的確定性模型。傳統的確定性模型包含2類：

1）若每種需求情形發生的概率為1，將3種需求情形分別代到確定性模型中單獨求解，得到3種不同的解，將這個解按照本文中的概率分布加權求和，即期望最優成本。但每一種情形下求得的樞紐選擇可能不同，樞紐選擇是航空公司的戰略選擇，較長一段時間內不會隨需求而變。

2）不同需求以一定概率發生，求得3種需求的期望值，將這一期望需求作為平均需求代入確定性模型可以得到一個最優的網絡成本。

這2種模型，第1種成本上占優，但是若要達到最優成本，必須要視需求變動樞紐選擇，對公司長期發展不利。因此本文中比對第2種確定性模型和DEP模型之間的成本和樞紐選擇的差異，如圖6所示。圖中虛線上的樞紐表示確定需求下的選擇，實線上的樞紐表示不確定需求下的選擇，可以看出當折扣因子相同時，需求確定和不確定兩種情況下樞紐選址結果存在差異，且不確定需求下的網絡總成本更低。

圖6 需求不確定和確定下的結果差異Fig.6 Differences in results under uncertain and certain demand

4 結 論

1）從航空公司的角度出發研究樞紐航線網絡的選址問題，考慮OD需求的隨機性和樞紐機場容量多水平決策，基于機場容量包絡曲線，構建了隨機需求下有容量限制的多分配、非嚴格的兩階段混合整數隨機規劃模型，并將兩階段模型轉化為確定的等價規劃。

2）在考慮機場容量限制時，為了讓模型更加貼近實際，將機場的容量表示為到港和離港航班的函數，繪制機場容量包絡曲線，獲得樞紐機場的容量限制。

3）對運輸成本折扣因子進行靈敏度分析，結果表明在不同的折扣因子情形下選擇的樞紐機場不同，折扣越大，選擇的樞紐越多，網絡總成本越低。當折扣因子一定、需求不同時，OD的運輸路徑有所差異，流量分配也不同。

4）通過對比需求確定和不確定下的結果差異，得出需求不確定下的網絡總成本更低。說明隨機規劃模型更能適應航空公司的發展需求，幫助航空公司規劃布局航線網絡。