脈沖星方位誤差估計的TSKF算法

許強，范小虎，徐利國，王宏力，馮磊，*

（1.青州高新技術研究所 測試控制系，濰坊262500； 2.火箭軍工程大學 導彈工程學院，西安710025）

X射線脈沖星導航作為一種新興的天文自主導航，在深空探測、衛(wèi)星授時等領域引起了研究人員的極大關注并掀起了廣泛的研究熱潮［1-3］。由于使用脈沖星發(fā)出的輻射信號作為信號源，X射線脈沖星導航相對于其他導航方式具有信號穩(wěn)定、抗干擾性強及自主程度高等特點，能夠較好滿足太空衛(wèi)星、深空探測器等航天器的任務需求。雖然目前相關國家針對X射線脈沖星導航的研究已經(jīng)進入了實驗驗證階段，但距離真正的工程應用仍然有一定的距離。其中一個較為重要的影響因素即為脈沖星存在的方位誤差問題。

由于大氣層對X射線信號的衰減作用，地面只能收到脈沖星在射電頻段的極其微弱信號，所以為了得到較為準確的觀測數(shù)據(jù)，需要使用甚長基線干涉測量（Very Long Baseline Interferometry，VLBI）技術。這就導致目前對脈沖星的觀測不僅成本高，而且不同頻段的觀測精度只能保證在毫角秒（milliarcsecond，mas）量級［4-5］。但對于脈沖星導航而言，幾毫角秒的方位誤差都有可能帶來數(shù)百米的導航偏差。為此，國內(nèi)許多學者從組合導航［6］、魯棒濾波算法［7］等方面開展了相關研究。同時，孫守明等［8］也提出了基于信標衛(wèi)星的脈沖星方位誤差估計算法，以提高脈沖星的方位精度。文獻［9］采用增廣擴展卡爾曼濾波的方法對該算法進行了改進，考慮了實際存在的信標衛(wèi)星位置誤差的影響。但是，以上2種算法都未考慮脈沖星方位的自行速度。雖然孫守明等［10］在后續(xù)的研究中采用勻速（Constant Velocity，CV）模型，在算法中加入了脈沖星的方位自行速度，但仍未消除信標衛(wèi)星位置誤差的干擾。然而這部分干擾是無法避免且較為致命的。

若在CV模型基礎上繼續(xù)采用文獻［9］中的增廣算法解決信標衛(wèi)星位置誤差的影響，將會使得矩陣運算由4維變?yōu)?維。當對多個脈沖星同時觀測時會大幅增加運算負擔，還容易出現(xiàn)數(shù)值病態(tài)的問題。為此，本文設計了兩級卡爾曼濾波（Two-Stage Kalman Filter，TSKF）算法。該算法可以在不增加維數(shù)的情況下實現(xiàn)對系統(tǒng)偏差的在線估計，兼顧衛(wèi)星位置誤差和方位自行速度影響的同時，實現(xiàn)較高精度的方位誤差估計。

1 誤差影響

1.1 方位自行速度的影響

對于宇宙中的絕大多數(shù)脈沖星而言，其方位并非一成不變，而是存在一定自行速度的。研究人員認為產(chǎn)生自行的因素很可能是超新星爆發(fā)不是各向同性的［11］。這種自行短時間內(nèi)受觀測技術限制難以準確測出［12］，但長時間看又存在跟隨脈沖星自身運動產(chǎn)生突變的可能性，影響脈沖星導航的使用。

以澳大利亞國家天文臺（Australia Telescope National Facility，ATNF）提供的脈沖星數(shù)據(jù)庫為例，所有2 702顆脈沖星中，已知自行數(shù)據(jù)的有306顆［13］，且均具有一定的不確定度。其方位自行速度及其滿足1個σ標準差分布時不確定度情況分別如圖1和圖2所示。

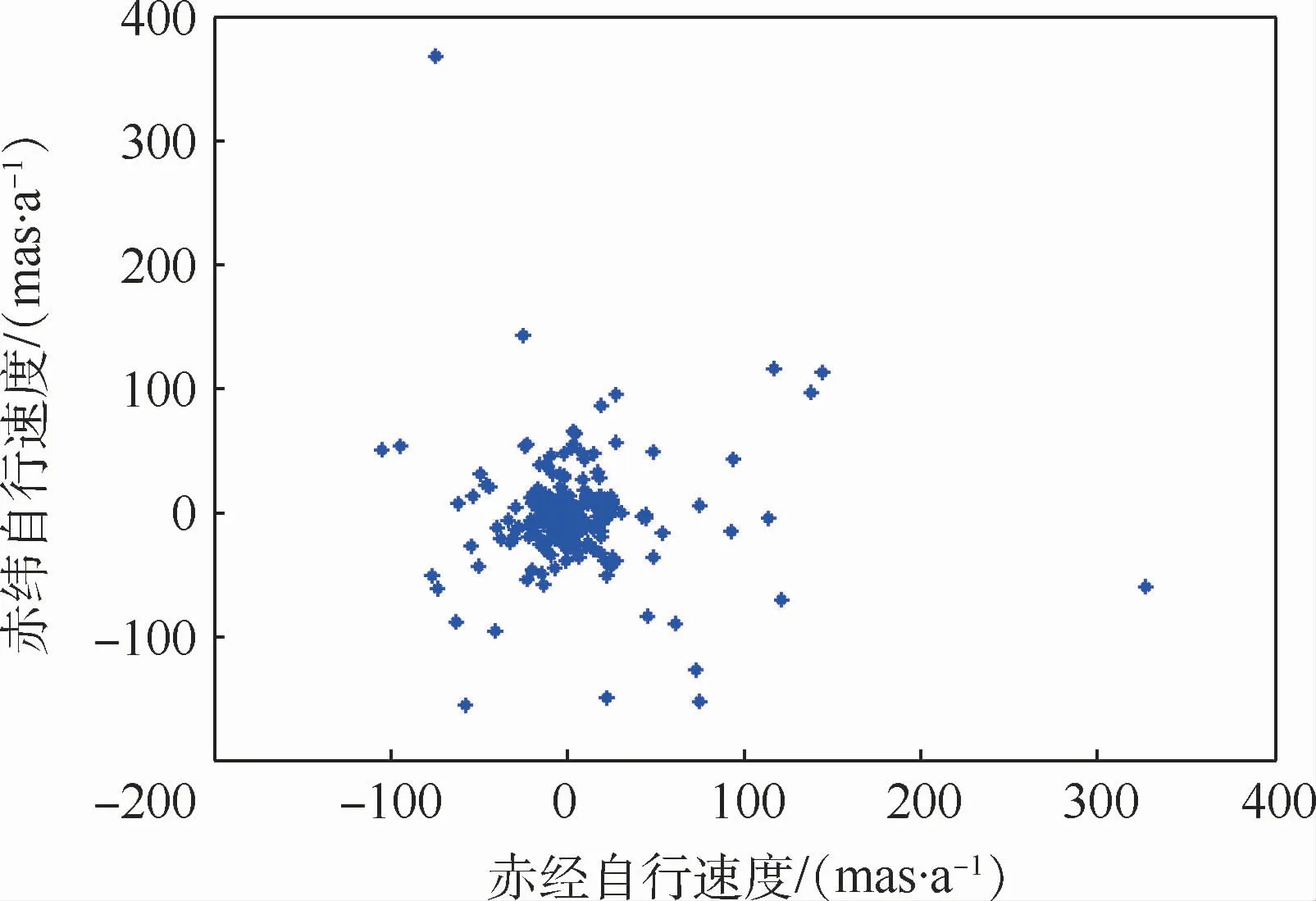
圖1 脈沖星方位自行速度分布Fig.1 Propermotion distribution of pulsars

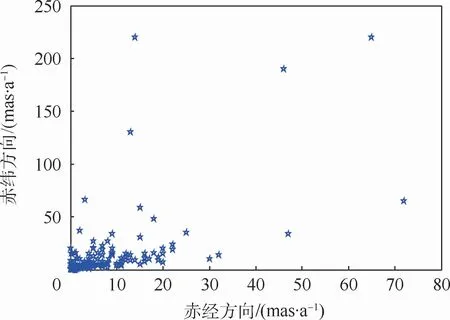
圖2 脈沖星方位自行速度不確定度分布Fig.2 Propermotion uncertainty distribution of pulsars

通過圖1和圖2可以看出，大多數(shù)脈沖星的赤經(jīng)、赤緯自行速度在50mas／a以內(nèi)，不確定度基本在10 mas／a以內(nèi)。如果在方位誤差估計中不考慮方位自行速度的影響，勢必會降低估計精度甚至產(chǎn)生發(fā)散。

以脈沖星B1821-24為例，其基本參數(shù)如表1所示。當使用文獻［9］中的增廣算法進行方位誤差估計時，假設探測器面積為1 m2，觀測周期為1 000 s，宇 宙X 射 線 背 景 流 量Bx＝0.005 ph／（cm2·s）（ph表示通過的光子個數(shù)），則觀測噪聲方差可計算得［6］σR＝（230.01m）2。使用同一衛(wèi)星軌道，分別在有方位自行速度和無方位自行速度的條件下進行導航計算。2種條件下衛(wèi)星的位置誤差均為［100，100，100］m，脈沖星的方位誤差為［2，2］mas。設定存在的脈沖星方位自行速度為［10，10］mas／a。具體仿真結果如圖3所示。

通過對圖3的分析發(fā)現(xiàn)，在無方位自行速度的情況下，增廣算法可有效隔離衛(wèi)星位置誤差的影響，進而實現(xiàn)脈沖星方位誤差的精準估計。但是存在方位自行速度時，估計算法會產(chǎn)生較大的發(fā)散，無法正常工作。

以上數(shù)值仿真說明，在對脈沖星方位誤差估計時有必要考慮方位自行速度的影響。

表1 脈沖星B1821-24參數(shù)Tab le 1 Param eters of pulsar B1821-24

1.2 衛(wèi)星位置誤差的影響

孫守明等［10］在后續(xù)研究中提出了基于CV模型的X射線脈沖星方位誤差估計算法。該算法將方位自行速度作為狀態(tài)量單獨估計，有效解決了方位自行速度的影響問題，但該算法并沒有考慮到衛(wèi)星位置誤差帶來的影響。

衛(wèi)星位置誤差對脈沖星方位估計的影響原理如圖4所示。當衛(wèi)星位置不存在誤差時，根據(jù)脈沖星方位誤差的觀測模型，可以認為脈沖信號到達太陽系質(zhì)心（Solar System Barycenter，SSB）處的時間延遲僅與脈沖星方位誤差有關。假設n為真實方向，～n為帶誤差的脈沖星方向，其滿足關系：

式中：Δn為方位誤差。

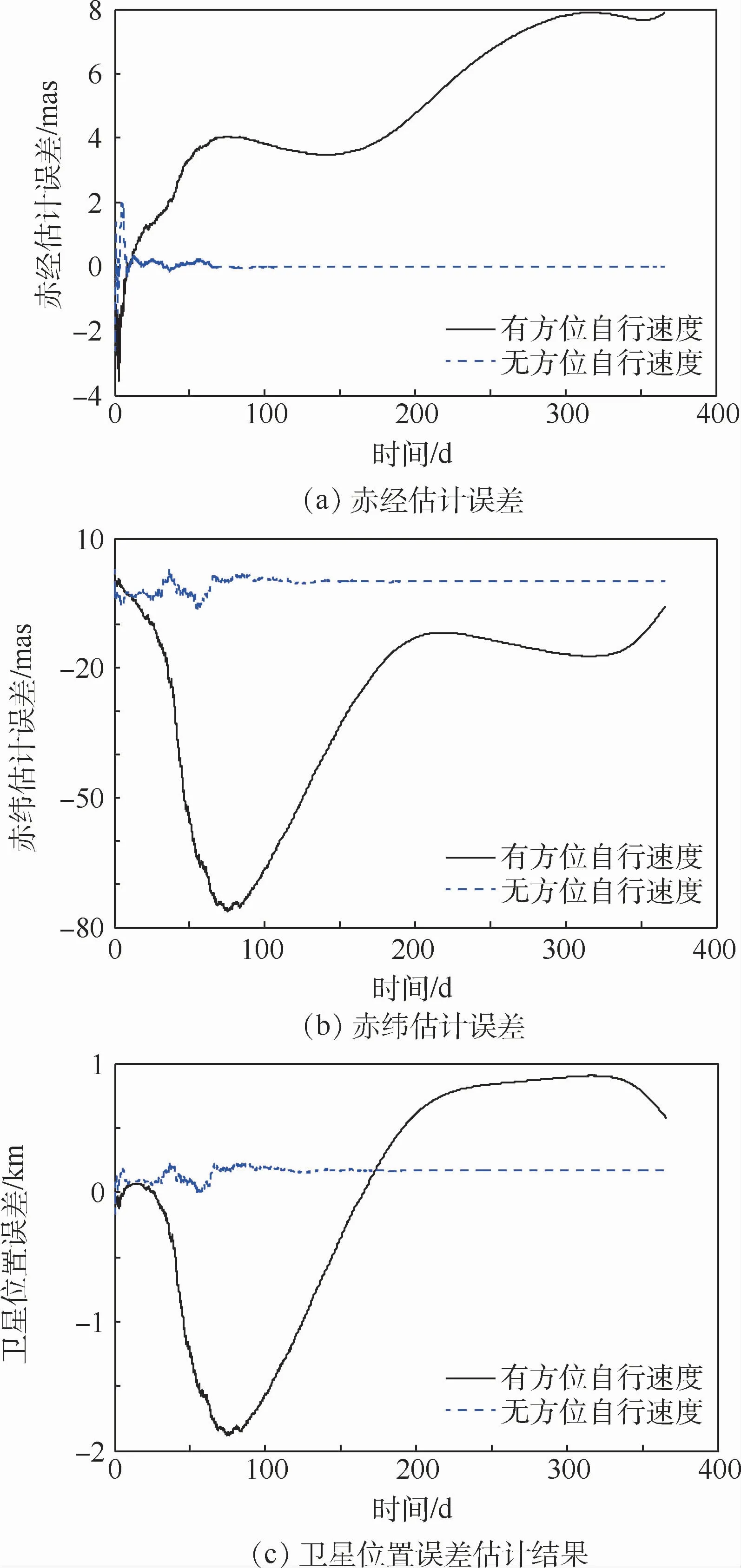
圖3 不同條件下增廣算法仿真結果Fig.3 Simulation results of augmented algorithm under different conditions

則觀測模型為［14］

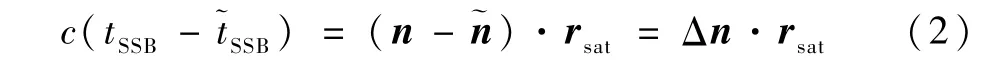
式中：c為光速；tSSB為真實SSB處脈沖到達時間（Time-of-Arrival，TOA）；～tSSB為根據(jù)觀測數(shù)據(jù)推算得到的SSB處到達時間；rsat為真實衛(wèi)星位置。

但若衛(wèi)星存在位置誤差Δr，在誤差影響下實際的觀測模型就發(fā)生了改變。存在Δr時，推算得到的到達時間＾tSSB與實際的到達時間tSSB之差就不再是單純的由脈沖星方位誤差導致。假設衛(wèi)星導航位置

＾r(nóng)sat與真實位置rsat滿足：

圖4 衛(wèi)星位置誤差對估計算法的影響原理Fig.4 Principle of influence of satellite position error on estimation algorithm

則此時觀測模型應當變?yōu)?/p>

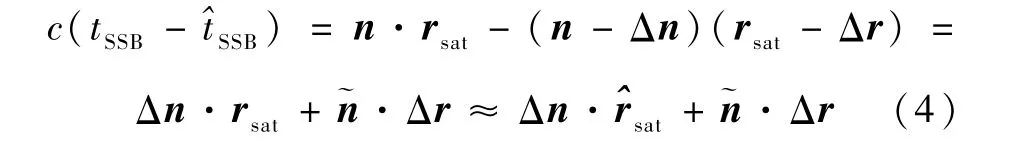
如果此時仍然以式（2）作為觀測模型，不僅會引入一定的系統(tǒng)偏差，還有可能在地球自轉(zhuǎn)的影響下產(chǎn)生發(fā)散。

同樣以脈沖星B1821-24為例，假設脈沖星方位誤 差 為［2，2］mas，方 位 自 行 速 度 為［10，10］mas／a。其他條件不變，采用基于CV模型的X射線脈沖星方位誤差估計算法分別在無衛(wèi)星位置誤差和有衛(wèi)星位置誤差情況下進行導航解算，衛(wèi)星位置誤差設為［100，100，100］m，具體仿真結果如圖5所示。

通過對圖5的分析可見，在加入衛(wèi)星位置誤差之前，基于CV模型的脈沖星方位誤差估計算法可以較為精準地估計出當前的方位誤差和方位自行速度。但是在引入衛(wèi)星位置誤差之后，由于地球的自轉(zhuǎn)，估計結果無法收斂在某一固定值。結合文獻［9］的分析，說明無論是否存在脈沖星方位自行速度，信標衛(wèi)星的位置誤差都應當成為估計算法重點解決的工程問題之一。

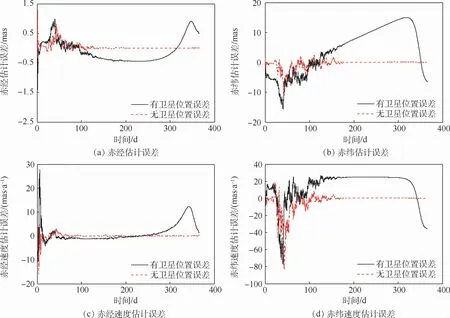
圖5 不同條件下基于CV模型的估計算法仿真結果Fig.5 Simulation results of estimation algorithm based on CV model under different conditions

2 TSKF算法

TSKF算法最早由Friedland［15］提出，用于解決線性系統(tǒng)中的定常偏差問題。Hsieh 和Chen［16］將兩級濾波思想用于標準卡爾曼濾波算法，證明最高可以將計算量降低59%。

本文在基于CV模型的方位誤差估計算法基礎上，采用兩級濾波的方法，將脈沖星方位誤差和方位自行速度作為第一級濾波狀態(tài)量，衛(wèi)星位置誤差作為第二級濾波的狀態(tài)量，在不增加狀態(tài)維數(shù)的前提下實現(xiàn)同步估計，有效隔離衛(wèi)星位置誤差對估計算法的影響。

結合CV模型和第1節(jié)的分析，可將TSKF算法的離散空間狀態(tài)方程寫為

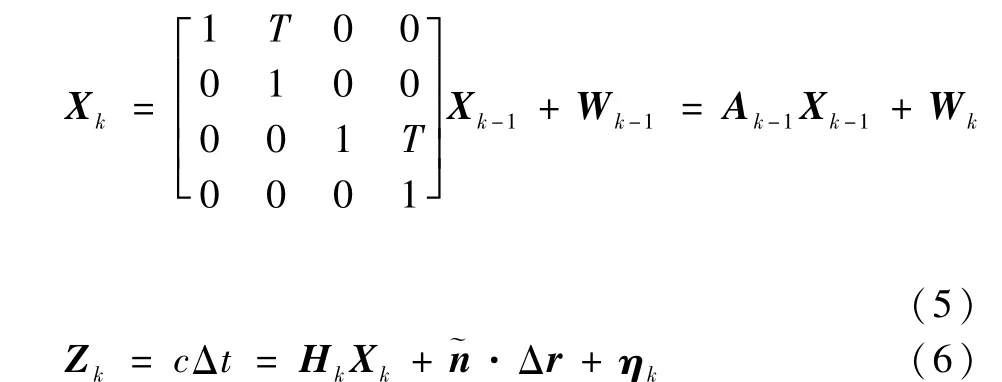
式中：Xk＝［ΔαkΔ˙αkΔδkΔ˙δk］T為第一級濾波的狀態(tài)量，分別代表赤經(jīng)、赤經(jīng)自行速度、赤緯、赤緯自行速度；T為計算步長；Ak－1為狀態(tài)轉(zhuǎn)移矩陣；Wk為系統(tǒng)噪聲；Zk為觀測量；Δt為脈沖到達航天器與SSB的時間差；ηk為觀測噪聲；Hk為觀測矩陣且滿足：

第二級濾波狀態(tài)更新：

分析以上過程還可以發(fā)現(xiàn)，TSKF算法的第一級濾波與常規(guī)的卡爾曼濾波算法完全相同，只是第二級濾波與一般濾波過程不同。實際上，在第二級濾波過程中公式Mk的作用是描述狀態(tài)量bk的估計方差，其對第二級濾波增益ˉKk的計算具有重要的影響作用。因此，式（14）相當于第一級濾波中的式（8），是估計方差陣的更新方程。在得到第二級濾波的增益矩陣ˉKk后，式（17）便相當于狀態(tài)量的更新估計，與第1節(jié)濾波中的式（10）作用相同，其中（I－ˉKkSk）bk－1為狀態(tài)量bk的一步預測，相當于第一級濾波中的式（7）。

而Vk的作用是糾正常值偏差bk對第一級濾波估計值Xk的傳遞影響作用，故可將其命名為糾正矩陣。由于第一級濾波估計中完全沒有涉及到常值偏差bk的計算，所以得到的估計值Xk必然是帶有一定誤差的。這部分誤差會隨著時間的推移而不斷變化。為此，在第二級濾波估計中，不僅要估計出常值偏差bk的值，還要利用式（15）實時求解當前的糾正矩陣。最后，通過式（18）將糾正矩陣Vk與第二級濾波估計值bk的乘積加到第一級濾波的估計結果中便實現(xiàn)了常值偏差與第一級濾波狀態(tài)量之間的隔離。第二級濾波時間更新環(huán)節(jié)中對矩陣Uk和Sk的計算均為計算糾正矩陣Vk的中間過程。

3 仿真分析

為證明TSKF算法的有效性，在方位自行速度及方位誤差都存在的情況下進行仿真驗證。所選用的脈沖星及其他相關參數(shù)與第1節(jié)相同。脈沖星方位誤差為［2，2］mas，方位自行速度為［10，10］mas／a，衛(wèi)星位置誤差為［100，100，100］m。

其他條件不變，將TSKF算法在不同衛(wèi)星位置誤差及方位自行速度條件下分別運行50次，其中每次運行的結果取為最后一天所有計算值的平均值。將每個算法運行50次的結果再取平均值作為此時該算法的最終精度。具體條件及誤差統(tǒng)計如表2和表3所示。

表2 仿真條件設置Tab le 2 Sim u lation condition setup

通過分析圖7、表2和表3可見，在不同誤差條件下，TSKF算法均可較好地完成收斂，并實現(xiàn)方位誤差最大約0.1mas及方位自行速度估計誤差最大約1.1mas／a的精度。同時，其收斂速度也明顯快于第1節(jié)提到的增廣算法和基于CV模型的估計算法。

考慮到實際衛(wèi)星在軌運行時，位置誤差可能根據(jù)軌道周期變化，故將衛(wèi)星位置誤差設置為隨衛(wèi)星軌道呈三角函數(shù)變化的形式。為體現(xiàn)普遍性，其具體關系式滿足：

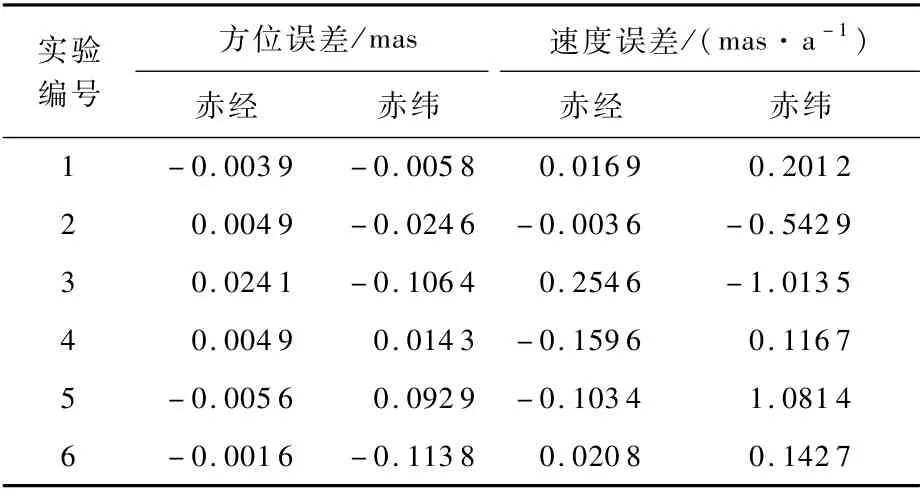
表3 仿真結果統(tǒng)計Tab le 3 Sim ulation result statistics

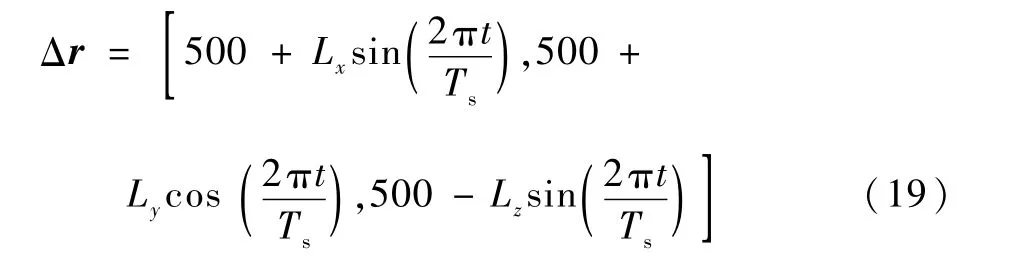
式中：Ts為衛(wèi)星軌道周期；t為衛(wèi)星運行時間；Lx、Ly、Lz為對應的幅值。

假設脈沖星方位誤差及方位自行速度同樣為［2，2］mas和［10，10］mas／a，則當Lx、Ly、Lz均為100m時，TSKF算法的具體運行過程如圖8所示。

采用同樣的統(tǒng)計方法，將不同Lx、Ly、Lz取值時的仿真結果統(tǒng)計如表4所示。

通過分析圖8可得，當衛(wèi)星位置誤差出現(xiàn)周期性的變化時只會導致曲線的“毛刺”愈加明顯。這是因為算法在達到穩(wěn)態(tài)后，位置誤差的周期變化相當于系統(tǒng)噪聲有所增加，所以TSKF算法的估計結果會出現(xiàn)“毛刺”增加現(xiàn)象。但從表4的結果來看，這對估計結果的影響非常的小。這是因為本文將一段時間內(nèi)估計結果的平均值作為最終的結果，消除了“毛刺”的影響。因此，若采取本文類似處理措施或在算法中添加相應的平滑處理環(huán)節(jié)，那么便可消除位置誤差周期變化的影響。

最后，為證明TSKF算法的高效性，將其與文獻［10］中4狀態(tài)量的基于CV模型的方位誤差估計算法進行對比。將仿真運行時間設為一個自然年，分別統(tǒng)計2個算法MATLAB程序中除參數(shù)初始化及觀測數(shù)據(jù)模擬部分的浮點運算次數(shù)。其中TSKF算法為30 045 202 038次，基于CV模型的估計算法為30 030 750 327次，前者僅比后者增加了0.048%，顯然比在CV模型的基礎上繼續(xù)采用狀態(tài)增廣的方法帶來的計算負擔小。

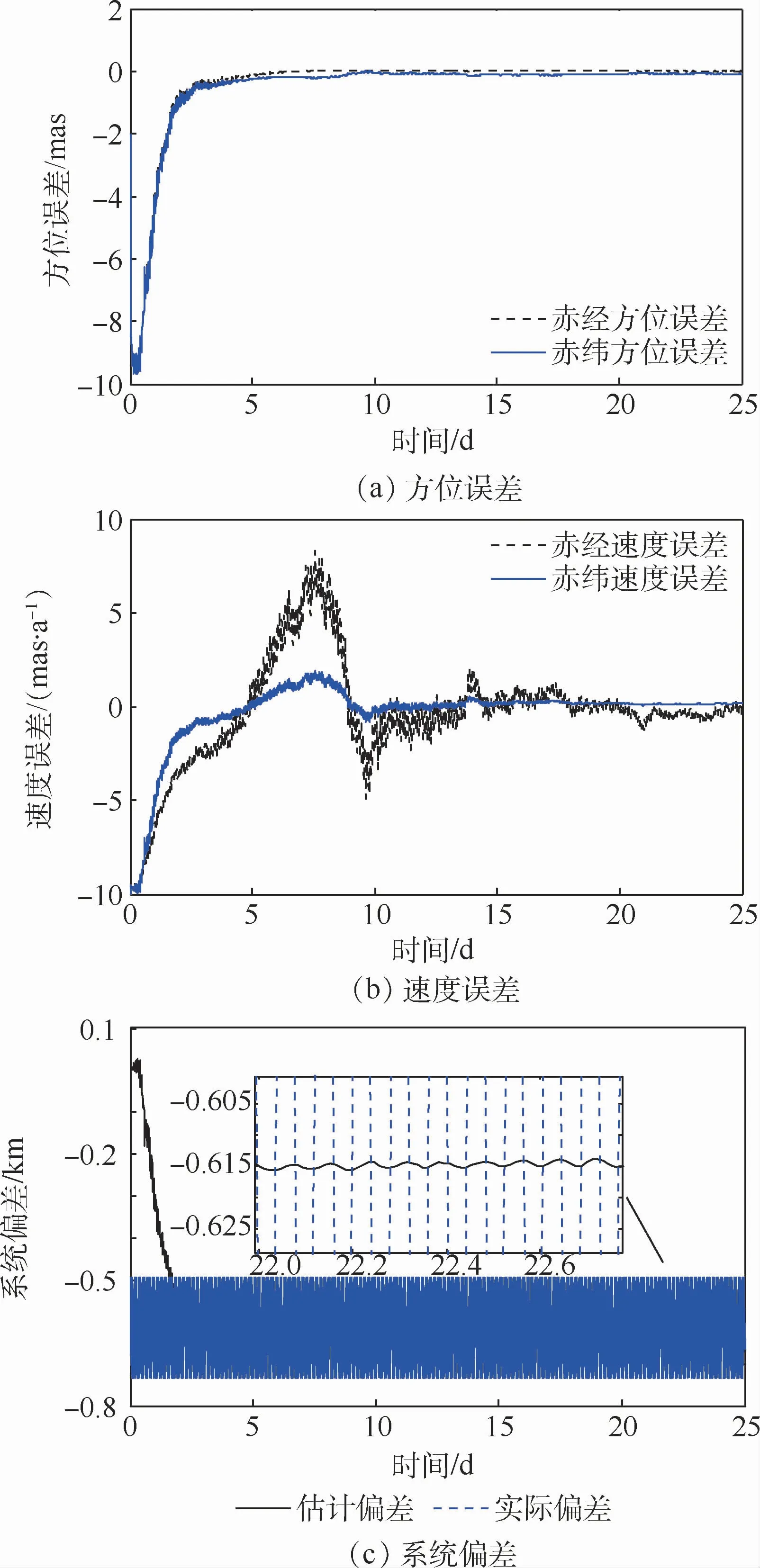
圖8 衛(wèi)星位置誤差周期變化時TSKF算法仿真結果Fig.8 Simulation results of TSKF algorithm when satellite position error period changes

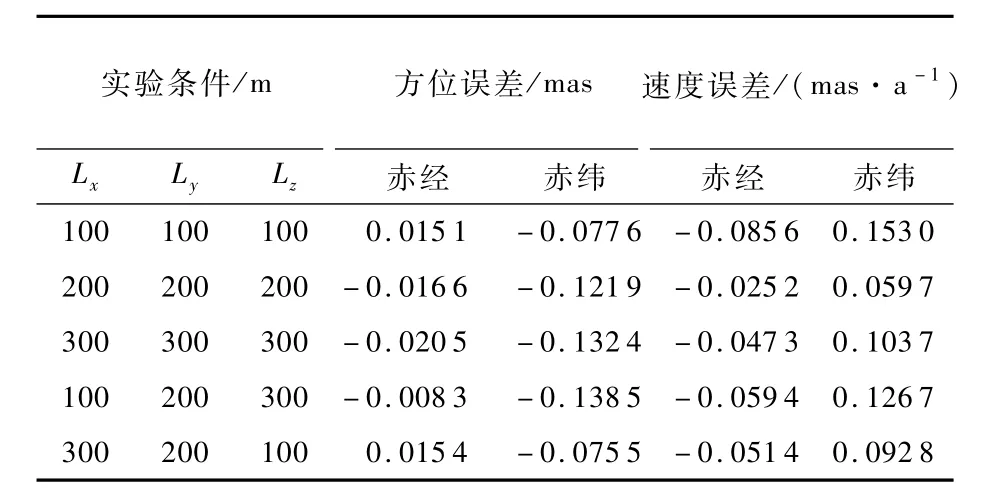
表4 衛(wèi)星位置誤差周期變化時仿真結果統(tǒng)計Tab le 4 Sim u lation resu lt statistics w hen satellite position error period changes

4 結 論

1）在脈沖星方位誤差估計中，方位自行速度和衛(wèi)星位置誤差均有必要考慮在內(nèi)，否則會嚴重影響算法的精度。

2）TSKF算法可以在方位自行速度和衛(wèi)星位置誤差都存在的情況下正常工作，并在仿真實驗中基本達到了0.1 mas的方位估計精度和1.1mas／a的方位自行速度估計精度。

3）TSKF算法的最大狀態(tài)量維數(shù)與基于CV模型的估計算法相同，且浮點運算數(shù)也僅增加了0.048%。相對于增廣的方法而言，兩級濾波的方法計算效率更高，更不容易出現(xiàn)數(shù)值病態(tài)等問題。