基于壓縮感知的高精度地磁基準圖構建方法

馬嘯宇，張金生，*，郝亮亮，李婷，王少博，李琳

（1.火箭軍工程大學 精確制導與仿真實驗室，西安710025； 2.火箭軍96863部隊，洛陽471000）

在近年來的導航技術發展過程中，衛星導航和慣性導航技術一直是飛行器導航技術的主流發展方向。但衛星導航的抗干擾能力較差，慣性導航的誤差隨時間不斷累積。地磁場隨時間變化緩慢且不受氣候、地域影響，且由于其無需主動發射探測信號、抗干擾能力強，地磁導航技術作為一種輔助導航方式逐漸受到關注［1-2］。

地磁匹配導航技術主要使用實時采集的地磁場數據與該區域地磁基準圖進行匹配［3-4］，從而實現定位。因此地磁基準圖的構建精確度對定位精度的好壞起著決定性作用。目前構建地磁基準圖的方法主要有2種：一是根據現有的地磁場物理模型進行構建；二是根據實測地磁場數據，構建網格化地磁基準圖［5］。現有國際地磁參考磁場（IGRF）和世界磁場模型（WMM）主要描述的是地球主磁場模型［6］。地磁場模型依賴衛星監測數據，地球內部異常場隨海拔高度升高而衰減，因此地磁場模型中幾乎不含異常場信息，用于刻畫局部地磁場時誤差很大，通過實測數據獲得的地磁基準圖具有更大優勢。目前，地磁基準圖的構建主要集中于插值法的研究，常用的方法有：三次樣條插值、Kriging插值［7］、基于粒子群優化（PSO）算法的Kriging（PSO-Kriging）插值［8］等。

現有插值方法存在的共同問題是在實測數據量較小時誤差較大，而壓縮感知理論能夠在采集少量數據的同時幾乎完全重構出原始信號，可以彌補在低采樣率下插值方法的缺陷。因此本文以現有的地磁場實測數據為基礎，利用信號處理中的壓縮感知理論進行地磁基準圖的構建，研究適用于地磁信息特征的壓縮感知算法，并驗證其在實測數據量較小時相比于傳統插值法的優越性。

1 壓縮感知理論

壓縮感知是2006年由Candes［9］和Donoho［10-11］等提出的具有革命性的信號處理理論。壓縮感知理論指出，當信號在某個變換域上是稀疏的，就可以投影為低維觀測向量，以遠低于奈奎斯特理論的采樣頻率進行信號采集，同時能夠高精度甚至完全重構出原始信號［12］。其核心思想是在信號發送端進行壓縮采樣，并在信號接收端進行高精度重建的過程，目的是在保證信號精度的同時大幅度提升信號采集的效率并降低采集成本［13］。壓縮感知理論主要分為稀疏表示和信號重建2個部分。設一個信號x（x∈RN×1），在基底Ψ 下表示為信號α，即x＝Ψα。若α中只有K個元素非零或其他元素趨近于零，則稱該信號在基底Ψ 下是K稀疏的，Ψ 稱為稀疏字典。

若能找到合適的觀測矩陣Φ∈RM×N（K＜M?N）對信號x進行采樣，則可得到M 維觀測信號為

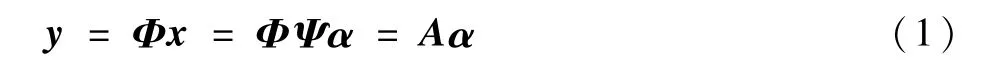
式中：A為傳感矩陣。即已知觀測信號y，求解出稀疏信號α，從而得到初始信號x。

觀測信號的維度M大于α的稀疏度K，因此可證明存在唯一解，即在已知壓縮矩陣Ψ 和觀測矩陣Φ時，根據低維信號y必然可解出原始高維信號x。因此實際上該問題可轉化為在一定稀疏度條件下求解最小L0范數解的問題，即

式中：b為原始信號；A＝ΦΨ。顯然Ψ 和Φ 共同決定了變換后信號的稀疏性，Ψ 與Φ 的差異越大，得到的解α就越稀疏。因此定義Ψ 與Φ 的互相關性為

2 稀疏字典

現有常用的稀疏字典有離散傅里葉基、離散余弦基、離散小波變換基、Curvelet基、冗余字典等［15］。

2.1 離散傅里葉變換

離散傅里葉變換將二維信號利用一系列周期函數進行表示，實際上是從時域轉化到頻域進行分析，離散傅里葉基可表示為

2.2 離散余弦變換

2.3 離散小波變換

離散小波變換是對于連續小波的尺度和平移進行離散化，在圖像處理方面有顯著的應用效果。本文采用Haar小波變換作為小波基。二維小波變換過程如圖1所示。

圖1 二維小波變換過程Fig.1 Two-dimensional wavelet transform process

3 觀測矩陣

3.1 高斯隨機矩陣

高斯隨機矩陣是在壓縮感知中應用最廣泛的一種觀測矩陣，由于其具有很強的隨機性，只需觀測維度M滿足：

式中：c為常數即可高概率地滿足RIP條件。因此在壓縮感知算法仿真中一般使用高斯隨機矩陣作為觀測矩陣以達到較好的實驗效果。但由于構造矩陣時數據的連續性和隨機性，硬件上實現困難，因此難以得到實際應用。

3.2 隨機伯努利矩陣

隨機伯努利矩陣的性質類似于高斯隨機矩陣，由于其中每一個元素都服從伯努利分布，M≥cK lg（N／K）時以接近1的概率滿足RIP條件。相比于高斯隨機矩陣，由于其元素都為±1，更有利于硬件的實現。

3.3 稀疏隨機矩陣

稀疏矩陣構造方法為：在一個M×N的全零陣基礎上，將每一行隨機d個位置置1，其中d∈｛4，8，10，16｝，在保證一定的重建精度的條件下易于進行構造和實際實現。

3.4 循環矩陣

循環矩陣的構造方法為：首先構造隨機向量β，即β＝（β1，β2，…，βN）∈RN，β中的元素取±1，而后經過M 次移位操作構造出完整的矩陣，同時矩陣中每一個元素服從伯努利分布。由于可通過移位寄存器實現矩陣構造，具有較好的應用前景。

4 仿真結果與性能分析

為研究適用于地磁基準圖構建的壓縮感知方法，本文比較了多種稀疏基和觀測矩陣在地磁基準圖構建中的效果。稀疏基選擇離散小波基和離散余弦基，觀測矩陣選擇高斯隨機矩陣、隨機伯努利矩陣、稀疏隨機矩陣、循環矩陣以及單位矩陣。本文以美國地質調查局（United States Geological Survey，USGS）于2002年發布的北美地區地磁場異常數據［16］為基礎，結合IGRF計算得到的地磁主磁場強度，從而得到地磁總磁場實驗數據。實驗樣本為10張128×128網格具有不同起伏程度的地磁基準圖，選取區域大小都為約50 km×50 km，以保證基本涵蓋全部類型的地磁特征；使用觀測矩陣維度、圖像處理中的峰值信噪比（Peak Signal to Noise Ratio，PSNR）以及絕對誤差（MAE）和均方根誤差（RMSE）作為評價標準。由于在信號處理端無需考慮實時性問題，信號重構算法采用精度較高的壓縮采樣匹配追蹤（Co-SaMP）算法，通過不斷更新迭代原子提高精度。PSNR值計算公式為

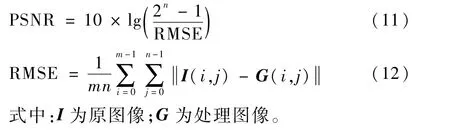
4.1 稀疏矩陣分析

以高斯隨機矩陣作為觀測矩陣，檢驗離散小波變換和離散余弦變換在不同維度觀測矩陣下的重建效果。圖2為離散小波變換和離散余弦變換重建效果隨觀測矩陣維度變化曲線，PSNR值為10張樣本圖分別重構后的平均值。可以看出，當觀測矩陣維度較大時離散小波變換重建效果較高，但隨著觀測矩陣維度的降低，其重建性能迅速降低，M＜50時幾乎無法重建信號；而對于離散余弦變換，M對重建效果影響較小，即使降到70，PSNR值依然可以保持在80 dB以上。

由于取的信號稀疏度K＝M／4，當M 減小時信號稀疏度也隨之減小。經過離散小波變換后的信號難以保證足夠的稀疏度，因此當觀測矩陣維度降低時會丟失大量的信息，造成重建信號的嚴重失真；而離散余弦變換可以保證足夠的壓縮率，能夠在保證一定重建精度的條件下降低觀測信號的維度。

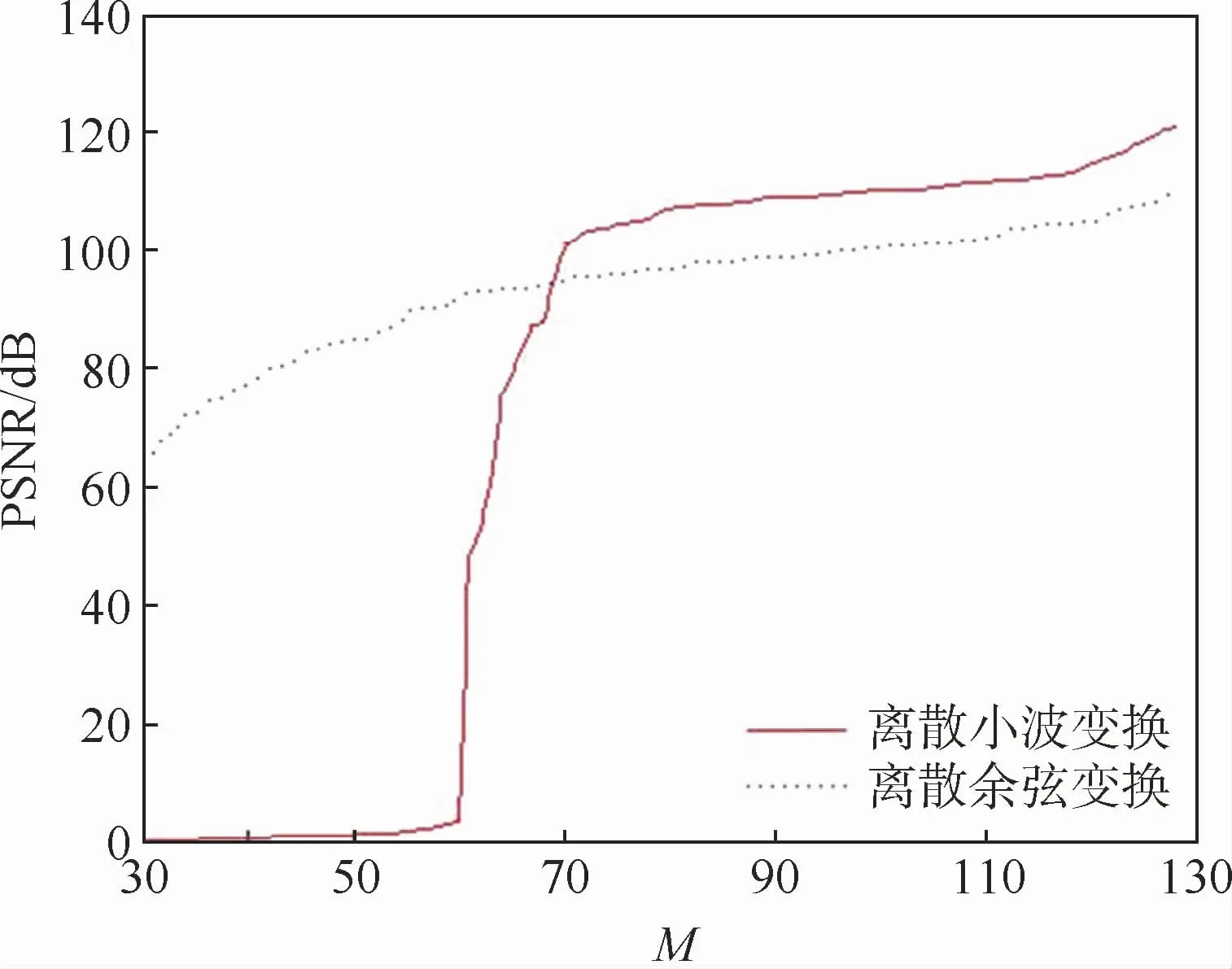
圖2 離散小波變換和離散余弦變換重建效果隨觀測矩陣維度的變化Fig.2 Variation of reconstruction effect of discrete wavelet transform and discrete cosine transform with dimension of measurementmatrix

4.2 觀測矩陣分析

為尋找適合地磁基準圖的觀測矩陣，以離散余弦變換作為稀疏矩陣，分別以高斯隨機矩陣、隨機伯努利矩陣、稀疏隨機矩陣、循環矩陣、單位矩陣作為觀測矩陣檢驗重建效果，實驗效果如圖3所示。

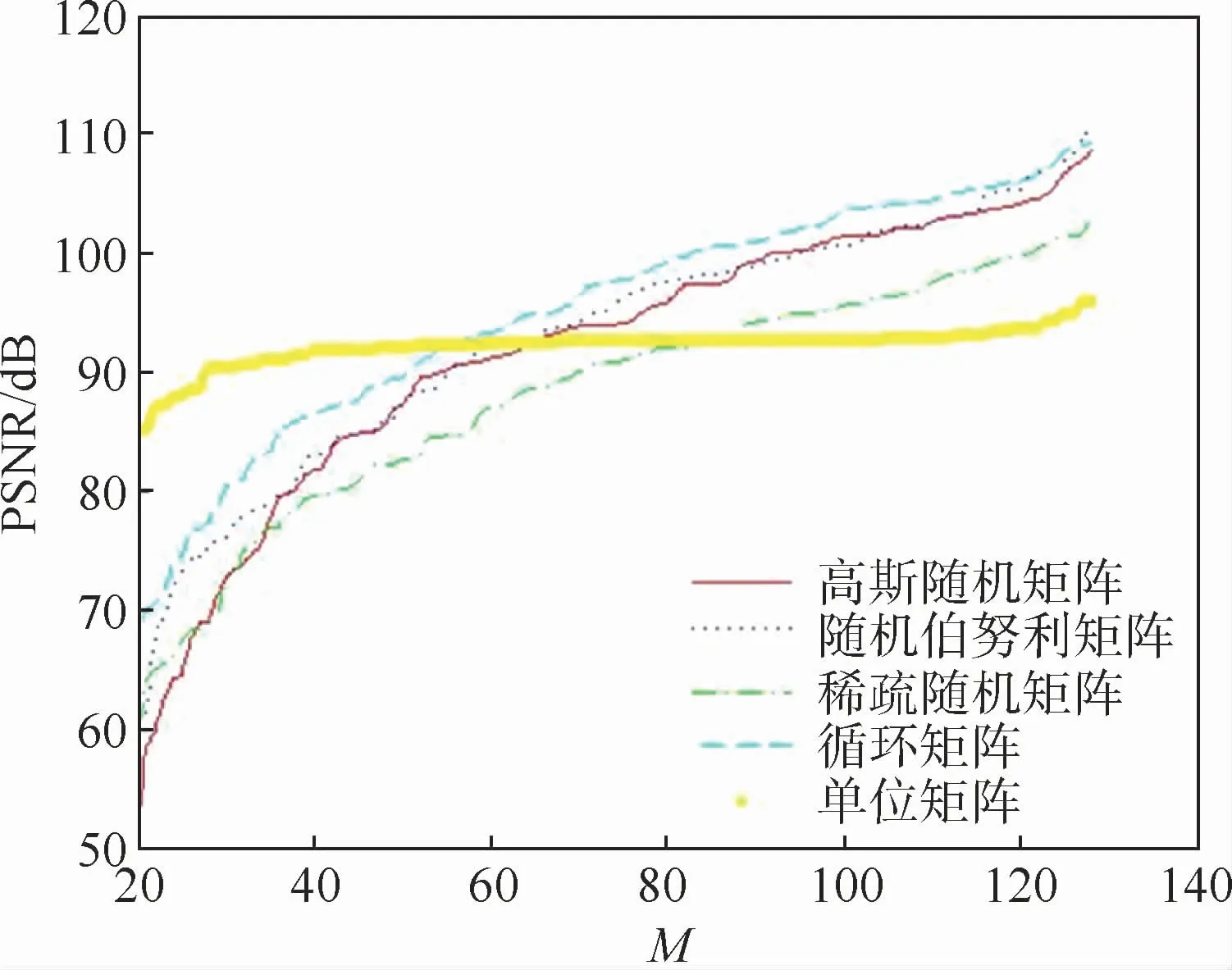
圖3 不同觀測矩陣重建效果隨觀測矩陣維度的變化Fig.3 Variation of reconstruction effect with dimension of matrix for differentmeasurementmatrices

從圖3可以看出，當觀測矩陣維度較大時，循環矩陣、隨機伯努利矩陣和高斯隨機矩陣都具有較好的信號重構效果；但隨著維度的降低，高斯隨機矩陣、隨機伯努利矩陣、稀疏隨機矩陣、循環矩陣的重構性能都迅速降低；在M＜55時，單位矩陣由于性能基本不受觀測矩陣維度影響逐漸體現出其明顯優勢。因此在保證一定重構精度條件下使用單位矩陣作為觀測矩陣能夠減小觀測信號的維度。

為檢驗重建算法的穩定性，將采樣率設為30%，對每種觀測矩陣進行100次重建，重建效果如圖4所示。

以PSNR值的標準差（SD）作為判定重建算法穩定性的標準，計算結果如表1所示，在30%采樣率下，利用單位矩陣作為觀測矩陣，在重建精度和穩定性都優于其他觀測矩陣。

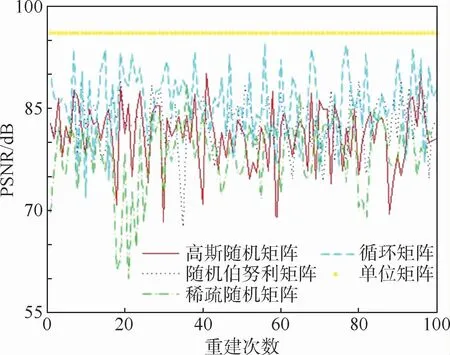
圖4 不同觀測矩陣重建穩定性Fig.4 Reconstruction stability of different measurementmatrices

表1 不同觀測矩陣重建100次PSNR標準差Table 1 PSNR standard deviation of 100 tim es reconstruction for d ifferentm easurem ent m atrices dB

4.3 與其他重建算法比較

為檢驗CoSaMP算法的效果，分別使用匹配追蹤（MP）算法、正交匹配追蹤（OMP）算法、分段正交匹配追蹤（StOMP）算法對30%采樣率下的地磁基準圖進行重建，以單位矩陣作為觀測矩陣，以PSNR值作為評價標準，實驗結果如表2所示。

4.4 壓縮感知與插值法比較

為驗證壓縮感知在地磁基準圖構建中的實際效果，將離散余弦變換及單位矩陣構成的傳感矩陣和三次樣條插值、Kriging插值、PSO-Kriging插值分別在25%、18.75%、12.5%、6.25%采樣率下的基準圖構建效果進行對比。

Kriging插值所采用的變異函數模型為指數模型，其具體形式為

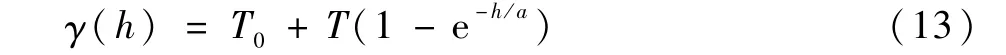
式中：T0為基臺值；T為塊金值；h為到插值點的距離；3a為變程。PSO-Kriging插值變異函數同樣采用指數模型，PSO算法粒子總個數設置40個，迭代次數設置100次。

具體采樣方法為：設128×128的原始地磁基準圖為P＝pij（i，j＝1，2，…，128），在25%采樣率（M／N）時，壓縮感知傳感矩陣維度選擇32×128，即M＝32在6.25%采樣率時，傳感矩陣維度選擇8×128，插值所用基準圖由隨機下采樣獲得，即保證所有方法采樣數據量相同。以PSNR值作為評價指標，結果如表3所示。當采樣率為25%時，壓縮感知與插值法的PSNR值基本相近，壓縮感知精度略高于插值法；當采樣率降到6.25%時，壓縮感知依然可以保持70 dB以上的PSNR值，明顯優于同采樣率下的插值法。

圖5為用壓縮感知和Kriging插值重建后的基準圖效果，可以看出Kriging插值后失去了很多細節信息，經過壓縮感知后圖像與原始圖相似度更高。

為充分驗證實驗結果的有效性，利用文獻［5］中的絕對誤差、均方根誤差和標準差3種性能指標進行分析。

絕對誤差為

表2 不同重建算法結果Tab le 2 Results of differen t reconstruction algorithm sdB

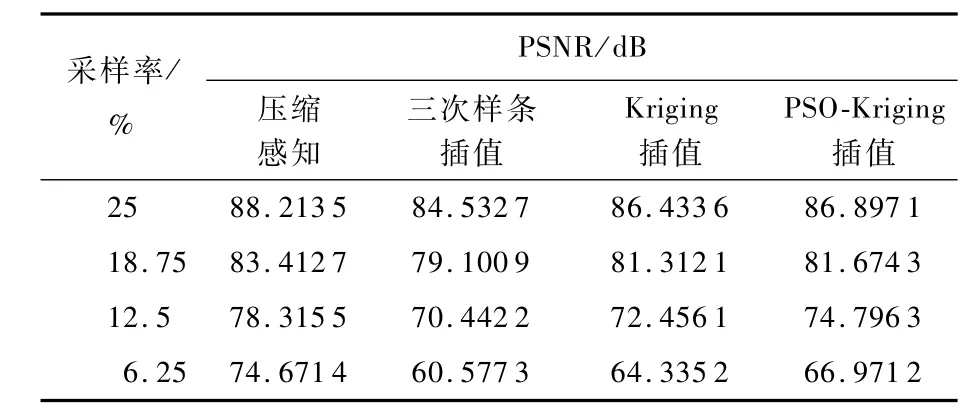
表3 不同采樣率下各方案構建基準圖的PSNR值Tab le 3 PSNR values of reference m ap reconstructed by different schem es at differen t sam p ling rates

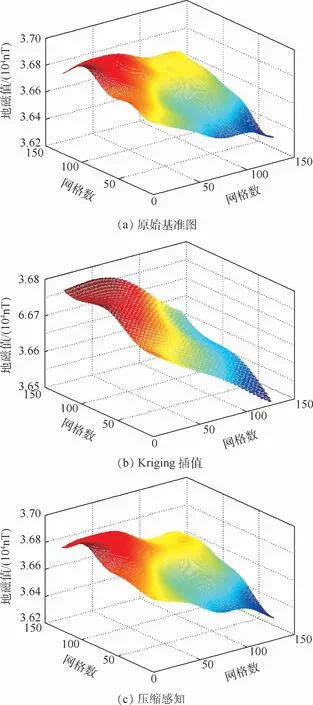
圖5 Kriging插值法和壓縮感知重構效果對比Fig.5 Comparison of Kriging interpolation method and compressed sensing reconstruction effect

均方根誤差為

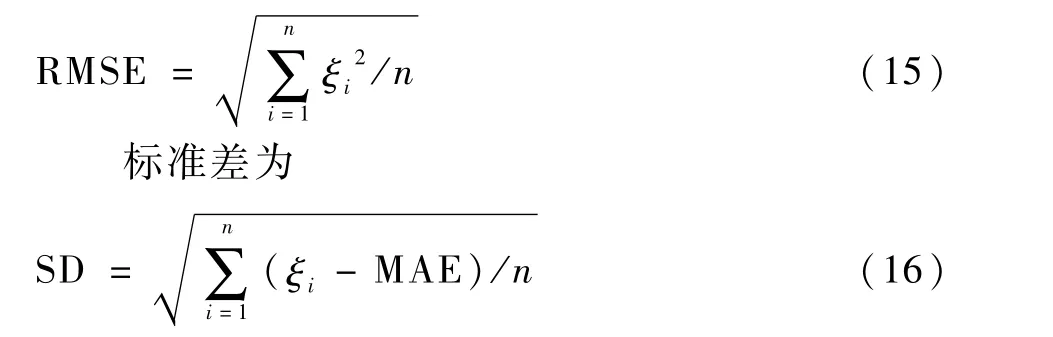
式中：ξi為真值與估計值之間的誤差。

為驗證各種方法構建效果隨采樣率變化情況，本文選取了25%、18.75%、12.5%、6.25%這4種采樣率進行實驗，計算結果分別如表4～表7所示。

從表4～表7可以看出，在各種采樣率下利用壓縮感知理論重構地磁基準圖性能都優于插值法，且采樣率越低優勢越明顯。

表4 25%采樣率下各性能指標數據Table 4 Perform ance index data at 25% sam p ling rate nT

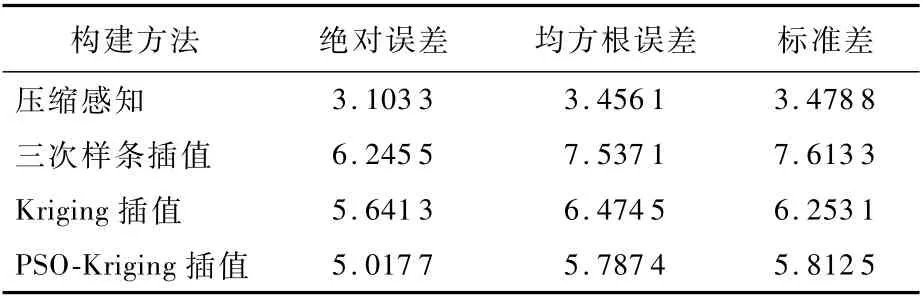
表5 18.75%采樣率下各性能指標數據Table 5 Perform ance index data at 18.75%sam p ling rate nT

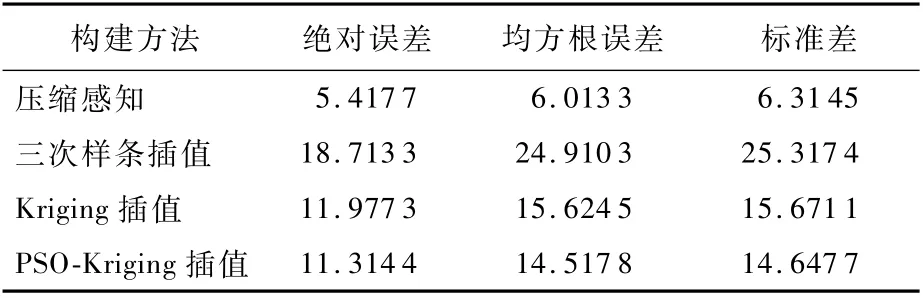
表6 12.5%采樣率下各性能指標數據Table 6 Perform ance index data at 12.5%sam p ling rate nT

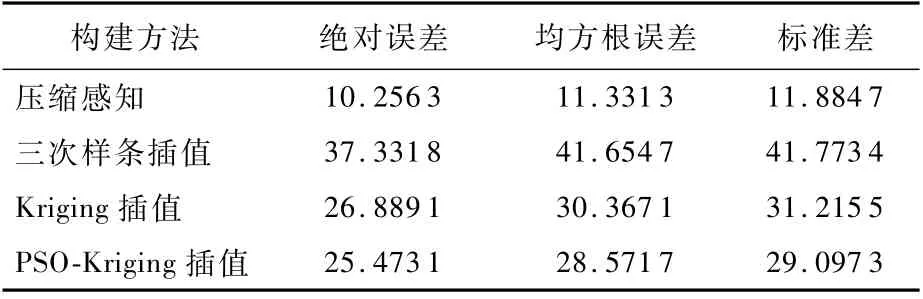
表7 6.25%采樣率下各性能指標數據Tab le 7 Perform ance index data at 6.25%sam p ling rate nT

5 結 論

1）驗證了壓縮感知理論在地磁基準圖構建中的可行性以及穩定性。

2）確定了以離散余弦變換作為稀疏基、單位矩陣作為觀測矩陣，以CoSaMP算法作為重構算法的基于壓縮感知的高精度地磁基準圖構建方法。

3）仿真結果表明，在6.25%采樣率下通過壓縮感知理論重構的地磁基準圖PSNR值、平均誤差、均方根誤差指標都明顯優于插值方法。

4）根據壓縮感知理論，要想完成對信號的壓縮感知，首先要進行壓縮采樣，通過一個隨機矩陣控制采樣點選擇是否采集信號。這就需要重新設計一種地磁信息采集方案。

5）如何將壓縮感知理論實際應用到地磁傳感器設計中并設計低成本、高重構精度同時利于硬件實現的觀測矩陣將是今后的研究方向。