水上飛機水面降落全過程力學特性數值研究

趙蕓可，屈秋林，劉沛清

（北京航空航天大學 航空科學與工程學院，北京100083）

近年來，中國海洋事業在民用領域蓬勃發展，水上飛機因其有別于陸基飛機，具備在水面起降的特點，可以應對應急救援和軍用領域的特殊需求，故而使中國對水上飛機開發研制的需求日漸迫切。

水上飛機水面起降的能力是其最為典型的特征，性能上要求其具備水面短距起降的能力、良好的穩定性和著水性能［1］，在設計過程中必須考慮氣動力和水動力的共同作用。為得到良好的起降性能，水上飛機在設計階段便投入大量研究，主要涉及多相流、自由面捕捉和剛體六自由度運動等復雜問題的相互耦合。

水上飛機的發展可追溯到20世紀，發展初期，理論解析與實驗是研究水面起降等問題的主要方法。1929年，von Karman［2］將水上飛機降落時浮筒的沖擊載荷簡化為二維楔形體入水沖擊問題，并提出附加質量力的概念。1932年，Wagner［3］基于von Karman的工作對小抬升角的二維楔形體的垂向入水沖擊問題提出進一步的修正，考慮了邊界條件、水面涌起與噴濺等條件的加入。此后的諸多理論研究都是在Wagner的基礎上做進一步的修正，但是對附加質量公式的修正大都針對沖擊階段，過渡階段及浸沒階段卻不適用［4］。1945年，Mayo［5］首次引入了三維流動的切片理論，結合二維流動的理論解，提出水上飛機沖擊與滑水過程的理論分析并與試驗結果進行對比。1948年，Milwitzky［6］總結了水上飛機沖擊與滑水的切片理論，并對飛機運動過程進行了分析。1952年，Miller［7］把縱傾角固定的水上飛機沖擊與滑水的切片理論拓展到縱傾角自由情況下的切片理論。NACA早期開展了大量的水上飛機設計試驗，研究其氣動和水動特性，包括不同抬升角［8］、不同外形參數（如機身高度、船體斷階高度等）產生的影響［9］。中國特種飛行器研究所也做了大量實驗，近年來王明振［10］對水上飛機的水載荷試驗方法進行了探討，并根據試驗目的對比了六自由度和三自由度試驗的優缺點。魏飛和許靖鋒［11］介紹了飛機模型在拖曳水池開展水上迫降試驗的原理和方法。

隨著計算科學技術的快速發展，近年各種數值方法在水上飛機沖擊與滑水過程的研究中得到應用。與經驗公式的理論方法和費用昂貴、平臺搭建時間較長的模型試驗相比，數值模擬方法在成本和靈活性方面具備較大優勢，不僅可以提取沖擊載荷等重要參數，還可以詳細地展示相應的流場結構、運動狀態和壓力分布，為飛機設計提供參考。

當前，主要應用在該領域的數值計算方法之一是以SPH 為代表的無網格方法。2004年，EADS-CASA 的 Pentecote和 Kohlgruber［12］采 用SPH方法研究了飛機（剛體）水上墜毀多場耦合問題，分析得到由飛機底部產生吸力對結果的影響是不能忽略的。2006年，上海交通大學吳衛等［13］使用SPH方法對二維水下塊體下滑進行了數值模擬，得到了水面破碎和漩渦。SPH方法在自由面大變形問題的模擬中表現良好，但在模擬氣墊效應和吸力行為時表現尚欠，這對物體運動狀態和沖擊力預報的準確性有直接影響。

結合兩相流模型的有網格技術可以較好地模擬出氣墊效應和吸力行為。以有限體積法（FVM）為代表，FVM 結合VOF自由面捕捉方法已經成為一種常用的技術，其主要優勢在于能夠計算飛機水上運動過程中所承受的氣動力和水載荷，其中尾部吸力的捕捉對飛機運動姿態的影響尤為重要。2007年，Streckwall等［14］使用基于動量法的DITCH，基于RANS方程結合VOF捕捉自由水面的Comet，模擬不同尾部形狀機身的著水沖擊過程，并與實驗結果進行了對比驗證。2009年，北京航空航天大學陸士嘉實驗室劉沛清、屈秋林等［15］使用FVM結合VOF方法，用Fluent軟件模擬了ARJ21飛機在平靜水面上的水上迫降過程，較好地捕捉到水面的變形并提出了最佳迫降姿態。2013年，上海交通大學邱良俊和宋文濱［16］將總阻力拆分為水動阻力和氣動阻力兩部分，分別用Fluent和CFX逐步分解計算，再將2種載荷的模擬結果合并，同時代入當前給定的發動機拉力，通過迭代模擬水上飛機的起飛過程。2015年，北京航空航天大學劉沛清、屈秋林［17］等用整體運動網格（Global Motion Mesh，GMM）方法模擬了二維圓柱垂向入水和飛機水上迫降運動，迫降過程同時伴隨沖擊入水和水面滑行運動，模擬得到的壓力分布狀況和運動狀態變化歷程與實驗結果進行比對，結果對應良好，表明該方法解決此類問題具有較好的適用性。2018年，上海交通大學張浪等［18］采用VOF方法，用Fluent軟件進行模擬，并在每一步代入當前的發動機拉力，模擬了姿態角固定情況下飛機的起飛過程。西北工業大學段旭鵬［19］等在開源平臺OpenFOAM 兩相流動態解算器中添加了激勵盤來模擬螺旋槳的拉力作用，并求解了水上飛機以固定姿態角進行滑水運動的過程。

用數值方法模擬水上飛機水面降落的全過程存在以下幾個難點：①從觸水沖擊、水面滑行到滑行停止，該過程運動距離長，對于傳統的動網格方法而言計算域過大，而有網格方法本身又對網格精細程度有較高的要求，導致計算成本難以承受；②飛機在氣動載荷和水載荷共同作用下做六自由度運動，模擬時對計算的收斂性有較高要求，且要求其結果可靠。目前，很多研究將該過程設定為固定姿態角或者受迫運動來進行模型簡化，或者僅截取沖擊或滑水某一階段進行模擬。

本文采用了流體求解器、整體運動網格方法、VOF自由面捕捉和六自由度模型相結合的方法，模擬了水上飛機從水面上方沖擊入水到滑行基本停止進入漂浮姿態的自由運動全過程。該方法的優點在于：①避免了傳統動網格的變形重構過程，即避免了因運動姿態劇烈變化導致的網格畸變所造成的計算發散，同時大大降低了計算域即網格數量，降低計算成本的同時增強了收斂性；②傳統的變形重構網格需要采用非結構網格，而整體運動網格理論上可以使用全結構網格，結構網格在使用VOF方法時模擬效果有明顯優勢，在模擬精度要求不變的基礎上結構網格所需的網格數量可大幅減少。基于以上優點，本文選擇整體運動網格方法模擬某型水上飛機水面降落的全過程。

1 整體運動網格方法及其驗證

1.1 整體運動網格

整體運動網格的開發基于Fluent商業軟件中的動網格方法，其特征是整個計算域跟隨飛機做剛體運動。計算時采用地面坐標系，每一步的迭代網格節點坐標都會隨著飛機的運動更新，故而不需要配合滑行距離而擴大計算域，即省去了傳統變形網格的變形區域。其中水體并不跟隨做剛體運動，而是始終維持地面坐標系下規定的水面高度，通過UDF使用VOF邊界條件設置即可完成該設定。

VOF 模 型 由 Hirt、Nichols［20］和 Muzaferija等［21］提出，該方法可以捕捉多相流之間的自由交界面，其中各相流體之間不相容同一個網格中，各相的體積分數之和為1。假設第q相流體有一個體積分數αq，在某個網格中，當αq＝0時，則說明該網格中不存在第q相流體；當αq＝1時，則說明該網格中只有第q相流體；當0＜αq＜1時，則說明該網格中除了第q相流體外，還有其他相的流體存在。第q相流體的體積分數方程如下：

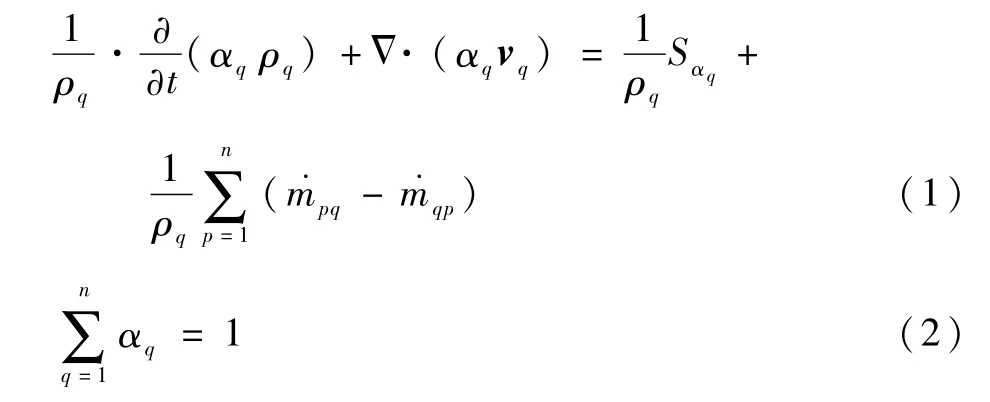
式中：ρq為流體密度；vq為流體速度；Sαq為質量源項；˙m為相間轉化質量流率。計算時，初始設置水面高度為0，水面以上水相體積分數為0，水面以下為1，水氣交界面為0.5。

六自由度模型通過求解平動和轉動方程來得到質心的位置和物體的姿態角。平動方程在慣性坐標系（地面坐標系）下求解。

式中：m為飛機質量；vg為重心的平動速度；fg為飛機表面力與重力之和；下標g表示地面坐標系。

轉動方程則在機體坐標系下求解：

式中：K為慣性張量；ω為飛機繞重心角速度；Mb為飛機所受繞重心力矩；下標b為機體坐標系。

1.2 計算格式

本文采用Fluent軟件作為計算平臺求解非定常RANS方程，采用增強壁面處理可實現k-ε湍流模型，壁面處采用增強壁面處理。壓力速度耦合采用SIMPLEC算法，壓力項采用體積力加權格式離散，動量方程中的對流項由三階MUSCL格式離散。湍流方程中的對流項由二階迎風格式離散，擴散項由二階中心差分格式離散，非定常項由二階隱式格式離散。本文中所有工況均采用此計算格式。

1.3 飛機水上迫降計算與實驗結果的對比驗證

為了驗證整體運動網格在模擬飛機入水沖擊過程中的精度和合理性，屈秋林等［17］針對NACATN-2929的模型F進行了水上迫降的數值預報，并與實驗結果進行了詳細的對比分析。實驗NACA-TN-2929［22］研究了不同外形的機身后段對迫降的影響，其中模型F機身軸線尾部上翹為寬機身，如圖1所示。

圖1 實驗NACA-TN-2929中的模型F機身模型［22］Fig.1 Fuselagemodel of Model F in NACA-TN-2929 experiment［22］

圖2 模型F的表面網格［17］Fig.2 Surface grid of Model F［17］

圖3 模型F的計算結果與實驗結果的對比［17］Fig.3 Comparison of calculation results of Model F with experimental results［17］

模型F的飛機表面網格如圖2所示［17］，采用半模計算，網格總量270萬。飛機位于半立方體的計算域中央，模型對稱面和計算域的對稱面重合，前端機身軸線和計算域上下邊平行，計算域上游邊界距離機頭2倍機身長度，計算域側邊界距離翼梢1倍機身長度。對稱面采用對稱邊界條件，外場邊界條件為速度入口。圖3［17］顯示了該工況的實驗結果與COMET數值模擬方法、DITCH動量方法和整體運動網格方法模擬結果的對比，總體上數值計算的模擬結果與實驗結果吻合度較高。其中，水平速度曲線顯示實驗結果的初始加速度很大，不同于模擬結果的加速度由小增大，而事實上模擬的結果更為接近真實情況。2007年，Streckwall等［14］進行模擬時也遇見了相同的問題，他們認為由于實驗年代較早，受限于測量手段實驗結果難免存在誤差。造成誤差的原因可能是水平速度的初始測量點選取在運動后的一段時間。

根據上述結果分析可見，整體運動網格技術在數值預報飛機水上迫降動態特性是合理可靠的。

2 某型水上飛機水面降落過程模擬

本節使用整體運動網格數值預報了某型水上飛機的水面降落過程。

2.1 模型信息和初始條件設置

如圖4所示，某型水上飛機的機翼參考面積約156m2，襟翼為簡單開縫式。起飛內外襟翼偏角20°，著水時內外襟翼偏角45°。機翼展弦比9，根稍比2.4，1／4弦線后掠角7.13°，船體前體長度14 m，斷階寬度2.7 m。本節分析了質量為49.8 t，轉動慣量為1.94×106kg·m2，以飛機頭部尖端為原點，重心位于前重心（15.91，0，1.15）m的某型水上飛機。設置初始運動狀態水平速度44.72m／s，垂向入水速度1.5 m／s，初始姿態角5°，重心距水面高度4.25m，斷階最低點距離水面高度1.15m。

計算模型為半模，飛機位于半立方體的計算域中央，模型對稱面和計算域的對稱面重合，前端機身軸線和計算域上下邊平行，計算域上游邊界距離機頭2倍機身長度，計算域側邊界距離翼梢1倍機身長度。對稱面采用對稱邊界條件，外場邊界條件為速度入口。飛機的中央翼盒、機翼和襟翼采用非結構網格，其余部分采用結構網格，可以確保水面基本處于結構網格中。網格數量約600萬，計算迭代步長0.01 s，共30 s。

圖4 某型水上飛機幾何特征和計算網格Fig.4 Geometric features and computational grid of a certain seaplane

2.2 數值模擬結果

如圖5所示，模擬結果展示了地面坐標系下的飛機姿態角、水平速度、重心距水面高度、垂向速度、過載和角加速度等變化歷程。其中過載是無量綱參數，垂向過載不包含重力作用的部分，定義如下：

式中：Fx為飛機所受水平過載；fx為飛機所受水平合力；Fy為飛機所受垂向過載；fy為飛機所受垂向合力；g為重力加速度。本文主要依據飛機運動狀態和過載的變化，將飛機整個降落過程分解為3個階段，即沖擊階段—滑水階段—漂浮階段。

1）沖擊階段。飛機具備一定的初始動能入水，沖擊造成的水載荷導致整體所受過載劇烈振蕩，且隨著動能的耗散振蕩幅度逐漸減小；該階段運動狀態參數變化劇烈，垂向速度呈現大幅振蕩，重心升沉幅度較大，期間可能發生彈跳（本文中即出現彈跳現象），并伴隨姿態角劇烈俯仰。

2）滑水階段。運動狀態參數振蕩幅度減小，飛機重心距水面高度變化先趨于穩定，后緩步下沉，此間不在發生彈跳或劇烈的俯仰。過載振蕩幅度較小，滑水運動產生的水動力主導運動姿態變化。

3）漂浮階段。所有參數隨時間發展趨于穩定，飛機的水面姿態接近靜水漂浮狀態，靜水浮力成為主要的外部載荷，垂向過載趨近于1（即外力作用主要為靜水浮力，其值接近飛機自身重力）。

2.2.1 沖擊階段

沖擊階段是飛機在水面降落的初始階段，該階段包含了飛機從接近水面到觸水沖擊的過程，主要作用在該階段的沖擊載荷是垂向的入水沖擊運動與水平方向的滑水運動共同產生的。由沖擊引起的大過載會導致飛機運動姿態產生劇烈變化，其中飛機觸水彈起現象是沖擊階段的典型特征之一。該階段從開始時刻持續到約4.8 s，定義重心距水面高度位置變化“峰-谷-峰”為一次沖擊過程，本工況沖擊階段共發生3次沖擊，命名為首次沖擊、第一次二次沖擊、第二次二次沖擊。圖6展示了沖擊階段飛機的運動狀態和過載的變化歷程。

1）首次沖擊

計算初期飛機自水面上方向水面迫近，觸水前作用于飛機的外載荷為氣動力。如圖6所示，從初始時刻到0.4 s左右，垂向過載約為0.8不足以抵抗重力，故指向下的垂向速度不斷增大，由初始的1.50m／s到最大2.53m／s；0.4～0.55 s尚未觸水，而向上的垂向過載開始增加。本文認為發生該情況的原因是飛機逐漸迫近水面時，機身底部與水面之間形成了一層空氣墊，氣墊效應使飛機受到了向上的壓力，故而垂向過載增加。0.55 s時姿態角為3.63°左右，而此前飛機已經展現出明顯的低頭趨勢，可見初始的低頭趨勢主要是氣動力造成的。

如圖7所示，為顯示清楚，壓力云圖的范圍為正負0.3倍大氣壓（圖中是相對標準大氣壓值，后同）。0.55 s時斷階最低點觸水，由入水沖擊產生的向上的垂向過載陡升，其峰值出現在飛機剛發生觸水的片刻后0.61 s，為1.68，這與通常水上迫降的載荷系數量級是一致的。隨著飛機的進一步下沉，下沉速度減小，垂向過載呈緩慢減弱趨勢，0.9 s飛機下沉速度降為0m／s時，飛機重心距水面高度位置到達最低點3.71m，此時斷階距離水面高度0.39m。此刻之后在垂向載荷的作用下機身開始第一次反彈，隨著重心被不斷抬高，機身入水體積減少，靜水浮力降低，垂向沖擊過載陡降，但依舊可以維持飛機向上彈起。2.07 s時重心處于第一次彈起的最高值4.78m，而后開始回落，回落過程中沖擊過載逐漸上升，開始第一次二次沖擊。

2）第一次二次沖擊

圖7 沖擊階段0.55 s水面狀況和機身底部壓力云圖Fig.7 Water surface condition and pressure contour of the bottom of fuselage at 0.55 s during impact stage

第一次二次沖擊和首次沖擊過程相似，但由于動能的耗散，過載和運動姿態的變化幅度都相較首次略有削弱。第一次二次沖擊從2.07 s開始，期間垂向過載峰值發生在2.82s，為1.32。當3.1s時重心距水面高度回落到最低位置4.04m，此時斷階距離水面高度0.07m。此后重心又開始呈現出上升趨勢，開始第二次彈起過程，第二次彈起過程與第一次類似，4.02 s到達第二次彈起的重心位置最高值4.29m，繼而回落開始第二次二次沖擊。

3）第二次二次沖擊

第二次二次沖擊的力度遠小于首次沖擊和第一次二次沖擊，從4.02 s開始到4.8 s結束，期間最大載荷系數在1.11。考慮到重心距水面高度回升后再未彈起到斷階離開水面的高度，故該階段并未包含“峰-谷-峰”的完整過程。此次沖擊之后沖擊階段結束，進入滑水階段。

在整個沖擊階段，角加速度和沖擊過載變化趨勢相似，故認為垂向載荷的作用對角加速度產生主要影響。圖8展現了從機身觸水到第一次彈起過程中，飛機機身底部壓力云圖。其中，前三張圖在機身斷階范圍處產生了明顯的負壓，即吸力。一般認為，斷階處發生的機身底部曲線大曲率變化是負壓產生的主要原因，當流動繞過這里時因為加速而產生相對負壓，這與水上迫降中得到的經驗相同［17］。結合圖6第三幅圖和第四幅圖分析可得，0.6 s沖擊發生時正壓主要作用位置在重心位置之前，斷階處則產生負壓，水載荷作用在飛機機身底部產生了很大的抬頭力矩，伴隨飛機姿態角顯著增大機尾逐漸下沉靠近水面；0.9 s時沖擊產生的正壓力減小，同時因為姿態角增大，機身下方正壓作用位置后移，使抬頭力矩減小；0.9 s后機身尾部開始入水，由于機尾距離重心較遠而且機尾在重心后方，盡管機尾處的沖擊過載較弱，仍然產生了較大的低頭力矩，直到1.2 s左右低頭力矩達到最大值，此后由于第一次反彈開始重心距水面高度上升，作用于機身尾部的正壓力減小，低頭力矩開始減小。從機身觸水開始到1.61 s期間飛機姿態角始終維持增大的趨勢，1.61 s時達到最大值10.72°；2.0 s時，飛機已經彈起離開水面，作用在機身底部的主要為氣動力。

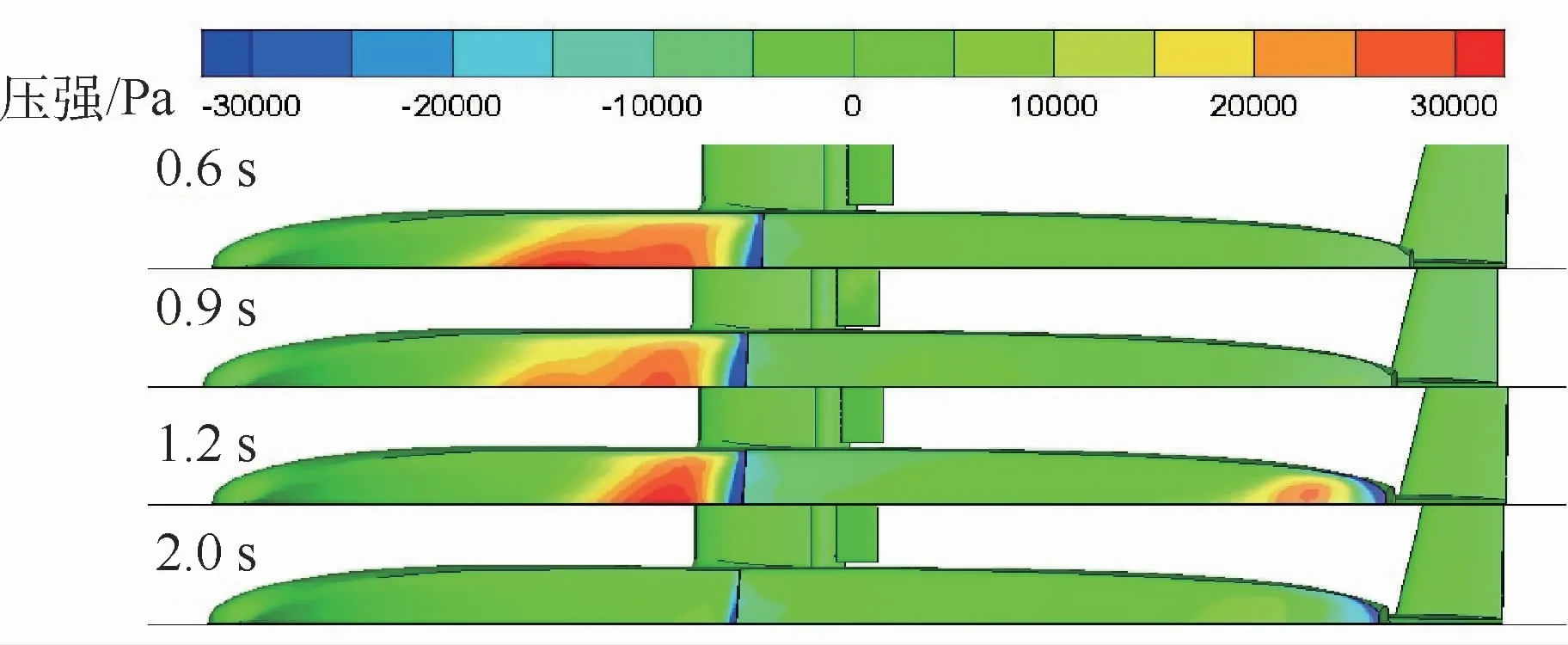
圖8 沖擊階段0.6～2.0 s機身底部壓力云圖Fig.8 Pressure contour of the bottom of fuselage for 0.6-2.0 s during impact stage

2.2.2 滑水階段

在沖擊階段的彈跳運動結束后，飛機垂向運動因為能量的耗散而不再對運動狀態構成主要影響，此階段飛機的水平速度依舊較大，故而滑水運動的影響開始占據主要地位。滑水階段的姿態角在前半程基本維持不變，后半程姿態角開始減小的該時刻為分界點，滑水階段被分為兩個階段，分別為機身后段未入水和機身后段入水，如圖9所示，這同時也解釋了姿態角變化的原因。

圖9 滑水階段運動狀態和過載變化歷程曲線Fig.9 Motion state and overload history curves during water skiing stage

1）機身后段未入水

在沖擊階段結束后，飛機進入滑水階段。由滑水產生的水平阻力降低水平速度，從而氣動力減小，飛機重心距水面高度下降，機身入水深度增加，水載荷開始承擔主要角色。滑水階段前半程主要滑行接觸面為包括斷階部位的機身前段，此階段姿態角基本維持在8.4°，一直持續到11.5 s。此時重心距水面高度位置緩慢下降，從4.09m下降到3.58m左右。

從圖10所示的機身與水面位置關系可以看出，滑水階段的前半段，機身尾部處于水面上方，飛機水平速度緩步降低但依舊保持向前滑行的運動，機身前方水面涌起并繞過機身，使上機身底部產生了一個沖擊載荷區，該沖擊載荷區的位置依舊在重心之前，伴隨著重心位置的下沉逐漸向機頭部位移動，但同時沖擊載荷降低，使該階段水載荷產生的抬頭力矩與氣動力產生的力矩恰巧維持了基本平衡，從而保持了姿態角的穩定。

圖10 滑水階段水面狀況和機身底部壓力云圖（機身后段未入水）Fig.10 Water surface condition and pressure contour of the bottom of fuselage during water skiing stage（tail does not touch water）

2）機身后段入水

如圖11所示，重心垂向位移呈現緩步降低的趨勢，11.5 s時刻機身尾部開始入水，產生了較大的低頭力矩，姿態角開始降低。同時機身后端入水使入水體積增加，導致12～13 s水平阻力增大，但逐步降低的水平速度又進一步限制了水平阻力的增加。

滑水階段的最后，重心距水面高度位置下沉至2.66m，垂向過載趨近于1，主要用于抵抗重力。

2.2.3 漂浮階段

當水平速度降低到一定程度，水平方向滑水運動產生的載荷逐漸失去主要位置，靜水浮力開始成為水載荷的主要構成部分。漂浮階段從17 s開始持續到最后。

圖11 滑水階段水面狀況和機身底部壓力云圖（機身后段入水）Fig.11 Water surface condition and pressure contour of the bottom of fuselage during water skiing stage（tail touches water）

圖12 漂浮階段運動狀態和過載變化歷程曲線Fig.12 Motion state and overload history curves during floating stage

如圖12所示，此階段的垂向過載趨于1，說明此時垂向除重力外，受力基本為靜水浮力；飛機保持慣性繼續向前滑行，并在水平阻力的影響下穩步減緩滑行速度，當飛機水平速度進一步變小，作用在重心前端的沖擊壓力減弱，其提供的抬頭力矩減弱，姿態角減小；隨著飛機姿態角的減小，機身前部逐漸入水，沖擊壓力區逐漸前移，但總體上沖擊壓力已經很弱，抬頭力矩不再隨之增加。整個過程中姿態角由4.32°降低至2.71°，最終逐漸接近飛機靜水漂浮時的姿態。圖13展示了此階段飛機的水面狀況。

圖13 漂浮階段水面狀況和機身底部壓力云圖Fig.13 Water surface condition and pressure contour of the bottom of fuselage during floating stage

3 結 論

本文利用整體運動網格技術結合VOF方法和六自由度模型，模擬了某型水上飛機水面降落的全過程，得到了較好的模擬結果，由此得到整體運動網格方法在解決水上飛機水面降落問題時具備良好的適應性。該方法計算成本低，穩定性好，模擬結果可靠，在處理長距離滑水問題時優點尤其突出。

本文的模擬結果展示了運動狀態參數和受力狀況的變化歷程，并結合壓力分布云圖和水面狀況，對水面降落過程進行定性與定量分析。本文將某型水上飛機在水面上降落過程劃分為3個階段，即沖擊階段、滑水階段、漂浮階段。各個階段的主要特征如下：

1）沖擊階段。飛機垂向的沖擊運動產生的過載主導該過程。該過程運動姿態變化劇烈，本文工況中出現的彈跳運動為該階段的典型狀況。

2）滑水階段。垂向方向的動能隨著沖擊很快被水的阻尼耗散，而此時仍然具有較大的水平速度，因此水平方向滑水運動產生的過載主導該過程。該過程中飛機重心距水面高度穩步下沉，運動姿態不再劇烈變化，而是在各載荷的相互作用下趨向穩定。在本文工況中，機身后段入水前滑水階段產生的穩定（相對于沖擊階段）沖擊壓力使得姿態角大小維持穩定，直到機身后段入水。機身后段入水后姿態角緩步減小。

3）漂浮階段。隨著水平速度的逐漸減小，滑水運動的作用減弱，靜水浮力接替主導位置。該階段沖擊壓力很弱，從而抬頭力矩減弱，姿態角逐漸下降，重心距水面高度幾乎不變，整體運動狀態趨于最終的靜水漂浮姿態。