無線傳感器網絡分布式分簇算法
徐 榮
(安徽廣播電視大學 信息工程學院,安徽 合肥 230022)
隨著無線傳感器網絡(WSN:Wireless Sensor Network)的發展,其以低功耗和低成本的特點,正在日益受到人們的關注,并被廣泛應用于不同的領域,如健康監測、汽車跟蹤等.隨著WSN 節點運行,節點能量消耗增加,如何提高WSN 傳感器節點能量的利用效率,更好地提高節點的使用壽命,是當前研究的重點.要解決該問題,關鍵在于構建一個合理的分簇路由協議,以此提高傳感器節點中不同節點的能量使用效率.而分簇路由協議的求解,本質是一個NP 難題.在這個難題中,要充分考慮最短傳輸路徑、最小能耗、拓撲結構簡單等問題.為解決該問題,譚軍(2015)、趙悅(2016)、冉涌(2019)等分別對無線傳感器的路由協議進行構建和改進,取得了豐富的經驗.但上述研究發現,WSN 網絡節點能量消耗還有進一步優化和提升空間.筆者在以往研究的基礎上,結合PSO(Particle Swarm Optimization)優化算法的優勢,主要從兩方面進行探討:一是構建傳感器節點能耗模型,二是對WSN 網絡節點中的簇首選擇問題進一步探討和優化.由此,結合上述兩方面的工作,解決WSN 中簇首節點能耗不均衡的問題,實現整個WSN 網絡節點能耗均衡的目的,提高整個網絡節點的使用壽命.
1 WSN 無線網絡節點傳輸能耗模型
1.1 網絡模型
出于對問題模型進行簡化的目的,將場景設定為長方形網絡區域,基站位于區域一側,各節點隨機分布于該區域內,見圖1.

圖1 WSN 節點網絡模型
該網絡中共有N個傳感器節點,其節點集合為V={Vi|i=1,2,…,N},各節點間連線的集合為E={(Vi,Vj)|(Vi,Vj)∈V*V,i≠j},則網絡拓撲結構可被抽象為無向加權圖G=(V,E).
若節點i 的坐標為(Vix,Viy),節點j 的坐標為(Vjx,Vjy),則節點i 與節點j 在二維平面上的距離為:

若節點的通信半徑為R,當節點i 與節點j 在二維平面上的距離d(Vi,Vj)不超過通信半徑R 時,則節點i 與節點j 互為鄰居節點.節點Vi的鄰居節點集合為S(Vi)={Vj|d(Vi,Vj)≤R}.
1.2 假設條件
根據研究需要,提出假設:
(1)隨機部署各個節點后,每個節點的位置始終保持不變;
(2)不考慮基站電量問題,各個節點為相同的初始能量,由自身電池提供;
(3)各個節點的計算、通信能力以及數據傳輸有效距離均保持一致;
(4)各個節點均有唯一標識,并且能夠獲取自身的位置和剩余能量信息.
1.3 能耗模型構建
在WSN 節點傳輸過程中,主要能量消耗來自節點對數據的發送和接收,且能量消耗隨著通信距離的增加而增加.當數據傳輸的距離為在d,發送的數據為l 比特比的情況下,其消耗的能量為:
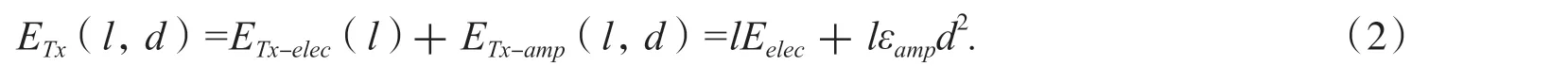
同時接收l 比特數據所需要消耗的能量為:

在公式(2)和(3)中,ETx-elec、ETx-amp表示監聽數據和信號放大所消耗的能量;ERx-elec、Eelec分別為接收器監聽耗費能量和節點接收與發送每比特耗費的能量;εamp為將單位比特數據廣播單位面積所耗費的能量.
但是上述的能量消耗模型沒有考慮距離的問題,即當傳輸距離足夠大的情況下.如考慮傳輸距離足夠遠,那么可以將上述的能耗模型轉換為:
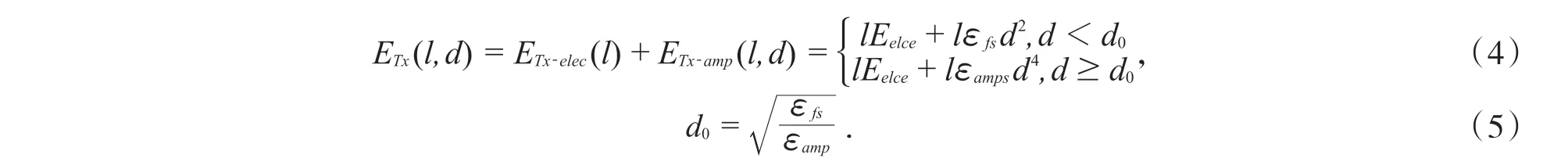
在該傳輸過程中,設置兩種傳輸模式,當d <d0時,則采用自由空間能耗模式;當d≥d0時,則采用多徑衰減能耗模式.
2 分簇路由算法
分簇路由算法的構建中,主要包括簇的建立和數據傳輸.其中,簇的建立階段主要考慮簇的數目、簇首能量消耗等因素,在數據傳輸階段主要考慮剩余能量.
2.1 最佳簇首
根據圖1 的節點分布圖,假設將該區域內的簇劃分為K 個,根據上述的能耗模型,得到簇首.而簇首的能量消耗ECH主要包括:接收簇類節點發送的數據消耗能量、接受節點成為簇成員耗費能量、廣播自己耗費的能量、數據融合以及融合后傳送耗費的能量.同時為簡化求解,都采用自由空間模型進行通信.由此,得到簇首消耗的能量:

簇內感知節點所耗費的能量ESN為:
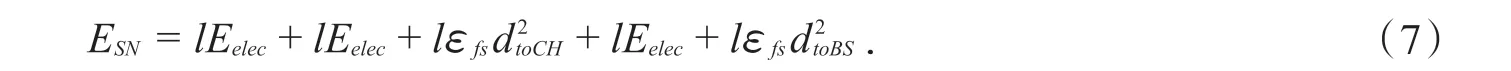
根據公式(6)和(7),得到節點工作一輪所耗費的總的能量:
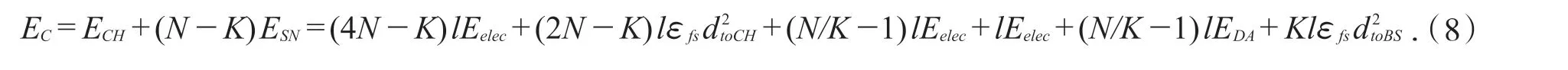
2.2 PSO 簇首優化選舉
筆者采用PSO 對最優簇首進行選擇,并連同節點所屬簇的相關信息全部發送到網絡.
2.2.1 粒子群優化算法基本原理
通過觀察研究鳥群覓食行為,發現在覓食過程中鳥群的每只鳥都在區域內隨機飛行進行搜尋,然后通過在鳥群中共享自身與食物的距離信息,使鳥群中的其他個體調整搜尋路徑,在距離食物最近的個體周圍進行搜尋.根據鳥群覓食行為提出相應的模擬算法,而實踐證明這是一種有效的優化,能夠得到復雜問題的最優解.在此基礎上不斷發展,最終由Kennedy 提出了粒子群優化算法.
假設在給定的目標搜索空間內有m 個粒子節點,粒子群集合為X={X1,X2,…,Xm},Xi=(Xi1,Xi2,…,XiN),i=1,2,…,m 為第i 個粒子的位置向量,通過適應值函數f(x)計算得到粒子當前的適應值f(Xi),然后可以根據f(Xi)的大小來判斷粒子位置向量Xi的優劣.其中,粒子節點數m 的大小直接影響著算法的收斂性和求解速度,應當根據需要解決的問題進行具體設定.
Vi=(Vi1,Vi2,…,ViN) i=1,2,…,m,Vi為 第i 個 粒 子 的 速 度 向 量.Pi=(Pi1,Pi2,…,PiN),i=1,2,…,m,Pi為第i 個粒子當前搜索到的最優位置,即個體極值為粒子群在第t 次循環后搜索到的最優位置,即全局極值pbestt.粒子在空間內跟蹤pbesti和pbestt進行搜索,直至達到設定的迭代次數或者誤差滿足設定條件.
每次迭代后,粒子群中的每個個體將更新自身速度和位置:
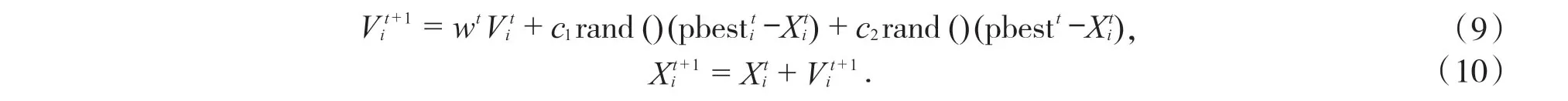
其中,c1和c2為學習因子,在[0,2]區間內隨機取值;rand()參數同樣在[0,2]區間內隨機取值;w為慣性權重.學習因子能夠使粒子群中的個體向優秀個體靠近;rand()參數能夠保證群體的多樣性;慣性權重能夠保證搜索的平衡.
2.2.2 適應度函數構建
為得到最優簇首,筆者以簇首能量因子f1、 簇內緊湊性因子f2、簇首位置因子f3、簇分布均勻性f4作為適應度因子.適應度值最小的作為最優簇首來選擇,即:
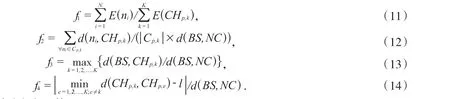
根據上述的因子,得到適應度函數:
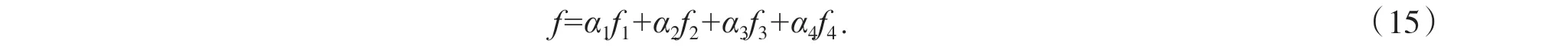
2.2.3 PSO 的適應度函數求解
要求解上述的適應度函數,采用PSO 優化算法進行求解.具體求解步驟如下:
(1)初始化粒子.根據上述的最優簇首計算方法計算網絡最佳分簇數Kopt,在粒子群X 集合中每個離子都包含候選簇首中的Kopt個節點,同時對離子的速度、位置等進行初始化.
(2)計算每個離子的適應度值,取適應度值最小的離子作為全局最優解gbest.
(3)更新粒子的速度和位置,使得離子能映射到具體的位置.
(4)更新全局最優和個體最優,再對每個離子的適應度函數值進行計算.
(5)適應度函數值如滿足設定的閾值,則終止,如不滿足,繼續更新粒子速度和位置,并進行適應度值計算.
在上述簇首優化的前提下,分簇路由算法見圖2.

圖2 最優簇首選舉
3 仿真實驗
為驗證上述算法的正確性和可行性,采用OPNET 軟件對上述算法進行模擬.同時為比較本算法的優劣,將本算法與傳統的LEACH 協議進行比較.仿真的實驗參數Eelec=50 nJ/bit,εfs=10 PJ/bit/m2,區域面積=100 m×100 m,節點數N=100,節點初始能量E0=0.5 J,d0=40 m,εamp=0.001 3 pJ/(bit·m4),數據包 長 度500 bytes,EDA=5 nJ/bit/signal,基 站 坐 標(50,50).整體節點分布見圖3.
通過上述的參數設置,經OPNET 軟件仿真,得到圖4 和圖5 的結果.
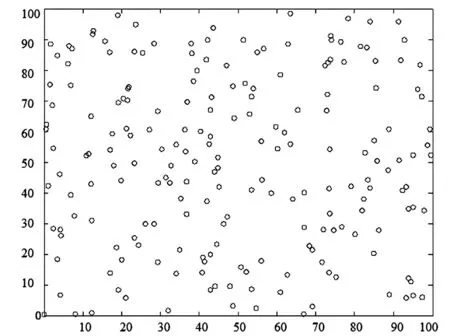
圖3 傳感器節點分布
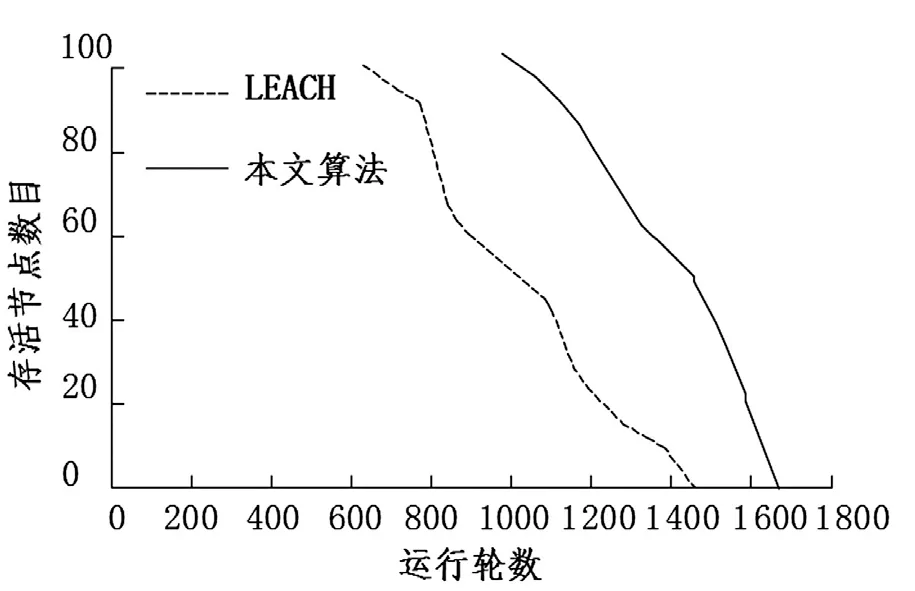
圖4 網絡節點存活數
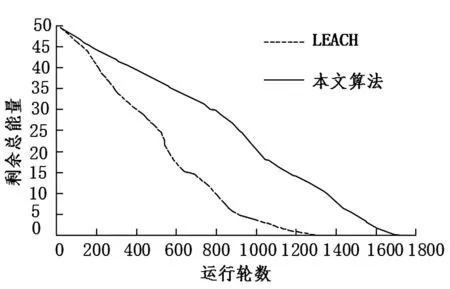
圖5 剩余總能量對比
通過圖4 的結果可看出,采用PSO 分簇算法得到的網絡節點存活數,從一開始就要高于傳統的LEACH 算法,并且第一個死亡節點比LEACH 分簇算法要推遲170 輪.由此說明,經過PSO 算法后,整個網絡要多工作兩百多輪.
圖5 為剩余總能量的對比圖.通過圖5 可看出,本文提出的算法,具有較小的坡度,而LEACH 算法坡度大.同時在運行輪數方面,本文構建的算法要運行輪數要明顯多于傳統算法.說明本文構建的分簇算法能耗更小.
4 結語
通過這些研究,分簇算法的本質就是一個NP 求解問題.在這個問題中,結合網絡的分布情況,選擇最優簇,即可在很大程度上減少數據傳輸路徑,并減少節點的能量消耗,進而最大限度的提高節點的使用壽命.而本文最大的特點在于,采用PSO 算法對簇首的選擇進行優化.

