直觀奇妙的“形數”
林革
所謂“形數”,顧名思義就是指有形狀可以構成圖形的數。相信許多讀者一定會感到奇怪:數怎么會有形狀呢?這得從其發明者—古希臘最著名的數學家畢達哥拉斯說起。
畢達哥拉斯研究數的概念時,喜歡把數描繪成沙灘上的小石子,而小石子又能夠擺成不同的幾何圖形,于是,就產生一系列的“形數”。譬如,當小石子的數目是1、3、6、10等數字時,小石子都能被擺成正三角形,這些數就叫“三角形數”;當小石子的數目是1、4、9、16等數字時,它們都能夠被擺成正方形,這些數就叫“正方形數”(如圖1)。
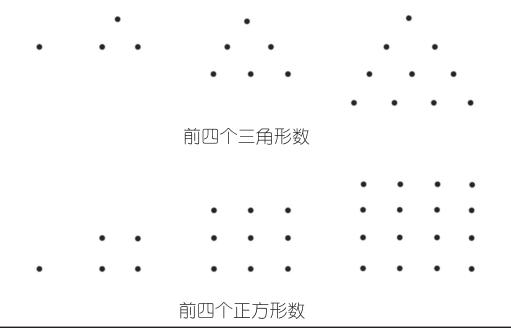
除此之外,畢達哥拉斯還擺出了多邊形數,并進一步發現了各種“形數”之間的內在聯系。由此,“形數”正式面世并引發了世人的關注。
羊群、石子和形數
有一天,畢達哥拉斯到郊外的一個牧場散步,遇到一位須發皆白的老翁正在那里牧羊。見了綠油油的草地,羊群四散開來,它們爭先恐后地啃食鮮嫩的青草。正在一旁玩石子的牧羊老翁認出身邊的人就是大名鼎鼎的數學家畢達哥拉斯,便與他閑聊起來。
其間,畢達哥拉斯隨口問道:“老先生,您放的這群羊一共有多少只?”
老翁望了望遠處的羊群,忽然眼前一亮,說道:“真是巧了!我的這群羊,除去待在我身邊的這只頭羊,其他的剛好是按1、3、5、7……分成若干群。最多的一群,我剛剛數了數,共有17只。至于總共有多少只嘛,大師,您能數出來嗎?”
見牧羊老翁并未直接回答,反而出了道難題,要考考自己,畢達哥拉斯也不多說,蹲下身,撿拾地上的石子。
“您是全希臘絕頂聰明的大師,請原諒我沒有直接回答您的問題。我就是想見識見識您的非凡智慧。”牧羊老翁解釋道。
“總共應該有82只吧。”畢達哥拉斯頭也不抬地答道。
聽了這話,牧羊老翁愣住了:沒想到,畢達哥拉斯這么快就算出來了!他不禁脫口而出:“這也太神奇了!”
牧羊老翁向畢達哥拉斯請教其中的玄機。畢達哥拉斯不慌不忙地擺弄起地上的石子,又用老翁牧羊用的鞭子在擺好的石子旁畫上方框(如圖2);然后,指著地上的圖形,解釋道:“您瞧,第一個方格里放了1塊石子,可以看作1=1×1;第二個方格里放的石子數是1塊和3塊,剛好有1+3=2×2;第三個方格里放的石子數是1塊、3塊和5塊,剛好有1+3+5=3×3;第四個方格里的石子數就是1+3+5+7=4×4;第五個方格里的石子數就是1+3+5+7+9=5×5……這就是用圖形直觀表示的‘形數。”
老翁恍然大悟,興奮地答道:“按照這樣的規律依次類推,1、3、5、7、……、17只羊共有9群,那么1+3+5+…+15+17=9×9=81,再加上我身邊的這只頭羊,總共就有82只羊。對吧?”
畢達哥拉斯點頭稱是。
“怪不得今天的羊群分布得如此奇特,原來就是為您的‘形數準備的啊!”牧羊老翁連連感嘆自己大開眼界,稱贊畢達哥拉斯名不虛傳。

三角形數和正方形數
畢達哥拉斯把自然數看成是點的集合,尤其對可以排成三角形、正方形的數情有獨鐘,因此,研究兩者之間的某些奇妙關聯就在情理之中。
眾所周知,自然數的構成是1、2、3、4、5、6、7、8、9、10、……“三角形數”實際上就是從1開始的一些連續自然數的和(參照圖1):
1、3、6、10、15、21、28、36、45、55、66、……、1225……①
“正方形數”實際上就是自然數a的平方a2:
1、4、9、16、25、36、49、64、81、100、……、1225……②

1、36、1225、41616、1413721、48024900……③
耐人尋味的是,如果對數列③繼續探究,便會發現,這類既是三角形數又是正方形數的數,是兩個正方形數的積的平方,可寫成一般式b2c2。譬如,

瞧,上面提到的b、c神奇地在分子、分母中悄然出現,讓人不得不瞠目驚嘆!
形數和數學公式
畢達哥拉斯利用“形數”發現了許多自然數的規律和定理,并直觀歸納出一些重要而常用的數學公式。下面擷取數則,以饗讀者。


三、求連續偶數的和的公式:2+4+6+…+2n=n(n+1)
形數操作:按每層的折線劃分,每個區域是連續的偶數2、4、6、8、10,剛好組成一個長方形數(如圖5),由此不難得出:2+4+6+8+10=5×6= 5×(5+1)。
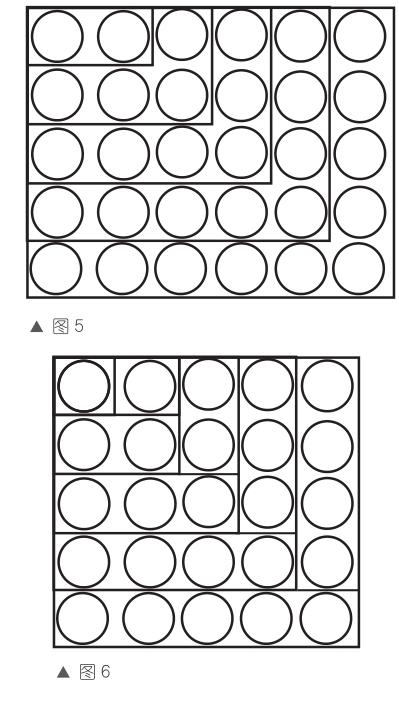
推而廣之,如果長方形數有n層,第n層就有2n個點,則有:2+4+6+…+2n=n(n+1)。


形數的奇妙性質
在三角形數和正方形數基礎上,如果把三角形數1、3、6、10、15、21、28、36、45、55、66……“一層一層疊加”,就形成了“四面體數”(所謂四面體,是指底面是三角形的錐體):
1、4、10、20、35、56、84、120……④
同樣,如果把正方形數1、4、9、16、25、36、49、64、81、100……“一層一層疊加”,就形成了“金字塔數”(所謂金字塔,是指底面是正方形的錐體):
1、5、1 4、3 0、5 5、9 1、1 4 0、204……⑤
有人突發奇想開始在⑤中探尋恰好是正方形數又是金字塔數的數,結果竟然只有一個,那就是4900。這令人頗感意外。不過,有關自然數、三角形數、正方形數、四面體數、金字塔數之間的奇妙性質,更讓人嘖嘖稱奇。
1.從1開始的連續自然數的立方和,等于相應的三角形數的平方。

3.任意兩個相鄰的四面體數的和,都是金字塔數。
譬如,四面體數④中,1+4=5,4+10=14,10+20=30,20+35=55,35+56=91,56+84=140,84+120=204;而5、14、30、55、91、140、204都是金字塔數。
或許,正是由于這些具有幾何特征的數字的奇妙特性,畢達哥拉斯和他所創立的學派崇尚“萬物皆數”,認為“數是萬物之源”。即用1表示點,用2表示線,用3表示面,用4表示體(如圖9),世間萬物皆由點、線、面、體所組成。而1+2+3+4=10,因此,10就可以表示宇宙。
用現代技術和知識進行評判顯然不夠客觀與科學,不過,畢達哥拉斯發明的“形數”確實讓人們認識到自然數的鬼斧神工和奇特絕妙,以上種種便是佐證。

形數的影響
“形數”之所以歷久不衰,引發關注,除了其巧妙利用數形結合和合情推理的特點之外,能夠充分反映出數學內在的奧秘和魅力似乎更具說服力。
需要說明的是,在公元前6世紀,紙張還沒有出現,所以,這種用小石子來研究數的性質的方法,不僅是認識數的一種簡潔而直觀的方法,更是古希臘人的一種偉大創造。正因為此,英文中的“計算”(calculation)一詞來源于拉丁字calculus,而calculus正是小石子的意思。這充分說明了西方人對畢氏“形數”的重視和尊重。就此而言,畢達哥拉斯非同凡響的思維和創新能力理應獲得我們的敬仰和欽佩。

