基于質心特征和重要敏感區域分類的分形圖像壓縮算法*

王 麗，劉增力

(昆明理工大學信息工程與自動化學院，云南 昆明 650000)

1 引言

隨著數字技術的發展，越來越多的信息通過圖像形式傳遞，對大量圖像數據信息進行高效的存儲和傳輸是當今信息時代所面臨的重要問題，除硬件本身需要改善外，高性能的圖像壓縮技術變得越來越重要。以分形為研究對象的分形幾何是現代數學的一個新分支，其本質是一種新的世界觀和方法論。

常用的圖像壓縮技術可以分為有損壓縮和無損壓縮2類，無損壓縮包括Huffman編碼、行程編碼、LZW編碼和算數編碼等，有損編碼包括預測編碼、JPEG編碼、變換編碼和矢量編碼等。2種類型的編碼滿足不同需求，無損壓縮完全保留圖像質量，而有損壓縮以犧牲一定的圖像質量，在確保恢復效果的前提下，大幅度提高了圖像傳輸速度和存儲量，面對大量的數據交互，具有廣闊的應用前景。分形編碼是一種有損圖像壓縮技術，它是圖像壓縮的一個重要工具。分形圖像壓縮利用了自然景物的自相似性來進行數據壓縮，以迭代函數系統為理論基礎。Barnsley等[1]最早給出了分形編碼的大致過程，即利用提取的分形子圖，尋找整體與局部之間存在的某種自放射特征。在實用化研究中，Jacquin[2]提出了分形塊編碼,通過對圖像的分割分別獲得互不重疊的小方塊和重疊的大方塊，然后對每個小方塊搜索與之最仿射相似的大方塊。Jacquin型編碼把分形編碼從“專家算法”變成“大眾算法”，分形編碼才真正被運用到眾多領域中。

2 相關研究

近年來，國內外涌現出越來越多基于Jacquin型編碼的分形圖像編碼技術。研究者主要從圖像分割方式、結合變換域、碼本縮減、匹配方式和解碼方式等方向展開研究，研究的目的都是減少分形編碼時間過長對編碼效率帶來的影響，以及確保重構圖像質量。基于變換域的分形圖像編碼方法在分形編碼之前對圖像進行處理，對處理后的圖像采用分形編碼，文獻[3 - 5]提出的分形與小波變換結合的混合編碼方法、謝敏等[6]提出的分形與DCT結合的混合編碼方法，都取得了良好的圖像恢復效果。Gupta等[7]提出的空域和頻域結合的方法，將塊分類轉換為空域分類，簡化了分類方式。結合其它編碼方式的混合分形編碼方法也被研究者嘗試，其中王春梅等[8]將算數編碼結合分形編碼的方法很大程度上提高了編碼效率。朱志良等[9]提出的基于像素的三角分割方式，可以對圖像不同紋理分布采取不同大小的塊分割，有效保留了圖像的重要信息。基于碼本縮減的分形編碼方法有很多，其中李高平等[10]提出的方差剔除條件的快速分形圖像編碼方法、何傳江等[11]提出的基于平均偏差排序的快速分形圖像編碼方法、Roy等[12]提出的基于縮放參數上限的方法，將原始碼本中不符合條件的碼本剔除，減少了匹配次數，編碼時間大大縮短。Ismail等[13]提出的結合布谷鳥搜索優化算法的分形編碼算法，改變以往傳統歐氏距離搜索方式，取得了不錯的效果。孔玲君等[14]根據人眼對圖像的視覺選擇特點，提出了感興趣區域壓縮方式，使得人眼對恢復圖像視覺效果增強，也間接地縮減了碼本。為了達到縮短編碼時間的目的，最直接的方式就是以圖像恢復質量換取編碼時間。相比直接剔除碼本，塊分類是一種折衷的方法，如汪瑋瑋等[15]提出的分類父塊方法、何傳江等[16,17]提出的叉跡特征分類方式以及張璟等[18]提出的雙交叉和特征分類方法，都實現了塊分類過程，達到了縮減編碼時間的目的。

本文提出一種基于質心特征和重要敏感區域劃分的分類算法，質心被廣泛應用于目標跟蹤和目標識別中，可以作為特征使用，本文將質心應用到灰度塊圖像匹配中，提取子塊不同的質心坐標，達到分類塊的目的。同時，考慮人眼對圖像的整體輪廓和部分細節較為敏感，以及對重要區域選擇關注的特點，對人眼視覺專注部分著重處理，增加圖像恢復好感度。

3 本文算法

3.1 基本算法

在基本分形編碼算法中，原始圖像首先被分割成互不重疊且大小為n×n的Range塊(簡稱R塊)和允許重疊且大小為2n×2n的Domain塊(簡稱D塊)。然后，將每個D塊通過4-鄰域像素平均算子壓縮為n×n的子塊，與R塊大小匹配，而所有壓縮后的D塊經過8種等距變換后就構成碼本Ω。

在編碼階段，對每一個R塊，按照全搜索方式在碼本Ω中尋找其最佳匹配D塊和自仿射變換ω，使得ω(D)與R的均方誤差均達到最小。為了尋找R塊的最佳匹配塊，需要求解下述極小化問題[19]：

‖R-(s·Dm+o·I)‖=

(1)

其中，m表示R塊的最佳匹配塊序號,s表示對比度收縮因子，o表示亮度偏移，I∈Rn×n是所有元素均為1的常值塊。

直接求解式(1)十分困難，耗時很長，為了降低復雜度，先忽略內層約束|s|<1，將極小化問題(1)轉化為下述問題求解：

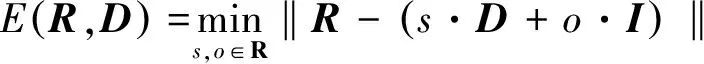
(2)

問題解為：

(3)

(4)

3.2 質心特征

分形編碼的絕大多數時間都是花費在R塊與碼本中D塊進行全局搜索匹配的過程中，特征算法的目的就是避開全局搜索，將搜索過程轉換成為局部搜索，每次搜索限定在一定特征下的有限區域內。

質心在幾何圖形中可以表示質量中心，即重心，對于規則的均勻物體，質心在其幾何中心，圖像同樣存在質心。下面證明在分形圖像壓縮編碼中，利用質心特征進行分類的可行性。假設子塊G，G(i,j)表示G中(i,j)處的值，其質心定義如下：

(5)

定義1子塊G=(G(i,j))∈Rn×n的歸一化定義為:

(6)

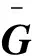
取歸一化后的值為特征值，定義子塊x和y方向的質心特征如下所示：

(7)

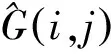
定理1對于R塊和D塊，設R，D∈Rn×n(n為偶自然數)，則有如式(8)所示的關于R塊和D塊匹配誤差的不等式成立：

(8)

其中，C′trx(R),C′try(R),C′trx(D),C′try(D)分別是定義的新質心特征。

證明過程見附錄。

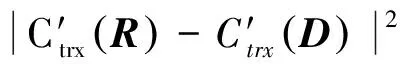
3.3 質心特征選取

用一個子塊的質心特征代表整幅圖像過于寬泛，因此本文采用求取R塊的多個質心的方法，聯合進行特征劃分。假設圖像塊X=(xi,j)∈Rn×n,n=8，如圖1a所示，將圖像塊X分為如圖1b所示的4個部分,Xk∈Rm×m,k=1,…,4，m=4，對每一個Xk求質心。大量的實驗表明，圖像質心分布于4個可能的位置，如圖1c中a、b、c、d所示。對于圖像塊X而言，質心的分布情況有44=256種。為了減少質心分類數，本文采用如圖1d所示的處在對角線位置的2個部分的質心作為分類標準，將質心分布情況減少到42=16種，從實驗中發現，圖像塊質心的分布具有相似性，往往分類不會達到16種。

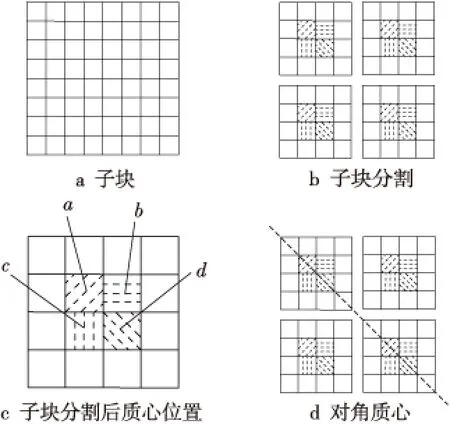
Figure 1 Centroid position圖1 質心位置

4 重要敏感區域劃分

4.1 敏感區域劃分

在分形圖像壓縮中，需要對圖像進行分割處理，與整幅圖像相比，子塊的結構比較單一，且往往在很多結構上具有相似性。通常根據R塊的結構分布可以將R塊劃分為不同的歸屬類，其中一個評判標準是方差。對于子塊而言，方差小表示該子塊像素值變化波動趨于平緩，即結構平滑；方差大表示該子塊像素值變化相對很大，即屬于紋理或邊緣等細節區域。

研究表明，人眼視覺系統對邊緣比對平滑區域更敏感，也就是說，人眼的注意力會更集中在提供信息的區域，對于圖像的邊緣、紋理、平滑區域，人眼敏感程度逐漸遞減。為此，根據人眼對圖像區域的敏感程度，將圖像劃分為敏感區域和非敏感區域。R塊在碼本中的最佳匹配塊一定與該塊最接近，包括灰度級的接近和灰度變化的接近，非敏感區域采用均值替代參數的方式，以此來縮短編碼時間。假設R塊的非敏感區域劃分閾值τ是固定的，R塊劃分方法如下所示：

σ<τ

(9)

其中,σ為R塊方差，若滿足式(9)即可認為R滿足非敏感區域條件，便用均值取代搜索匹配參數，否則認為R塊為敏感區域。

4.2 重要區域

人眼視覺能感覺到的重要區域一般為圖像的中心1/4部分，因此對這部分著重處理會增加人眼對圖像的好感度。這部分圖像往往會被第一眼看到，基于此，本文將原始圖像分為2部分，分別為中心1/4面積部分的重要區域和其余的非重要區域。對重要區域的編碼采用更加精細的匹配編碼，對該區域內的非敏感區域劃分使用的閾值τ′不同于式(9)中的閾值τ，二者滿足τ′<τ，這樣可以使得更多處在重要區域內的R塊進行全局匹配，進而使重要區域圖像灰度質量提高。重要區域劃分如圖2所示。

Figure 2 Sensitive area圖2 重要區域

5 算法分析與實現

對于輸入的R塊和D塊，由式(8)知，如果R塊和D塊的質心特征相差較大，則二者的均方誤差Ex(R,D)和Ey(R,D)也相差大，即整體均方誤差E(R,D)也會大，從而導致D塊不能與R塊匹配。對應地，如果D塊是R塊的匹配塊，那么二者的整體均方誤差就會較小。因此可以認為，如果R塊和D塊互為匹配塊，那么二者也是在質心特征下的近鄰。需要指出，R塊和D塊在質心特征下相差小，不一定代表E(R,D)也小，從而R塊和D塊在特征意義下的最佳匹配并不能保證D塊是R塊在最小均方誤差下的最佳匹配塊。盡管特征意義下R塊和D塊匹配不能保證均方誤差下二者的匹配，但是最佳匹配D塊距離也不會太遠。本文采用擴大搜索半徑的方法，在特征意義下以最佳匹配D塊為中心，距離L為半徑，步長K進行搜索，尋找更大范圍內的最佳匹配塊。

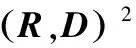
(10)

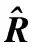
基于以上推導，本文算法的具體步驟如下所示：

步驟1將原始圖像分割成為不重疊的大小為n×n的R塊，以橫縱方向步長為Δ生成可重疊且大小為2n×2n的D塊，采用鄰域平均方法將D塊大小變為n×n，并構成碼本Ω。

步驟2將原始圖像劃分出重要區域和非重要區域，設置閾值τ′、τ、η、搜索半徑L以及步長K。

步驟3對重要區域使用閾值τ′進行敏感區域劃分。若R塊滿足σ<τ′，則認為其是敏感區域，求取并存儲其平均值aver作為參數；若R塊滿足σ>τ′，則認為其是非敏感區域。對敏感區域R塊在碼本Ω中進行質心特征匹配，尋找匹配塊Dm，以Dm為中心，L為搜索半徑，K為步長搜索最佳匹配塊D′m，并存儲參數。當滿足E(R,D′m)<η，搜索結束。

步驟4對非重要區域使用閾值τ進行敏感區域劃分。滿足σ<τ認為是敏感區域，求取并存儲平均值aver作為參數；滿足σ>τ認為是非敏感區域。對敏感區域R塊在碼本Ω中進行質心特征匹配，尋找匹配塊Dm，以Dm為中心，L為搜索半徑，K為步長搜索最佳匹配塊D′m，并存儲參數。當滿足E(R,D′m)<η，搜索結束。

步驟5對于所有R塊，重復步驟2～步驟4，其中將處在重要區域與非重要區域邊界的R塊判定為重要區域。

6 實驗結果與仿真

實驗中采用的圖像是Matlab標準庫中圖像，大小分別有256×256和512×512，R塊大小取用4×4，D塊大小取用8×8，D塊劃分間隔為8像素，半徑L為40像素，步長K為4像素，圖像恢復效果采用人眼觀察、峰值信噪比PSNR(Peak Signal to Noise Ratio)、重要區域峰值信噪比SAPSNR(Sensitive Area Peak Signal to Noise Ratio)、編碼時間、解碼時間和壓縮比進行評價。其中SAPSNR值作為重要區域的峰值信噪比[5]，即等于恢復圖像中心1/4部分的PSNR。

本文參考2種特征類似的算法，分別是張璟等人在文獻[18]提出的雙交叉和特征算法、何傳江等人在文獻[16,17]中提出的叉跡特征算法，以及基本分形圖像壓縮方法，對重要區域峰值信噪比(SAPSNR)進行對比；同時為了觀察圖像敏感區域恢復效果，計算恢復圖像子塊均方根大于4的部分的峰值信噪比。李高平等人在文獻[10]中認為均方根小于4的部分的子塊為敏感塊，對比實驗中采用統一閾值τ=4。本文算法非重要區域采用敏感區域閾值τ=4，對于重要區域閾值τ′=3。

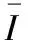
(11)

(12)

(13)

SAPSNR=

(14)

恢復圖像的壓縮比CR(Compression Ratio)的計算方式如式(15)所示：

(15)

其中，Num1表示圖像經過壓縮后傳輸過程中數據量，Num2表示圖像不經過壓縮直接傳輸所需要數據量。

表1所示為基本分形算法、雙交叉和特征算法以及本文質心特征算法的實驗結果，其中C代表Cameraman圖像，L代表Lena圖像，P代表Peppers圖像,PSNR(Sensitive area)代表恢復圖像中滿足敏感區域條件的PSNR值的和。從表1可看出，本文算法相比文獻中算法壓縮效果更好。

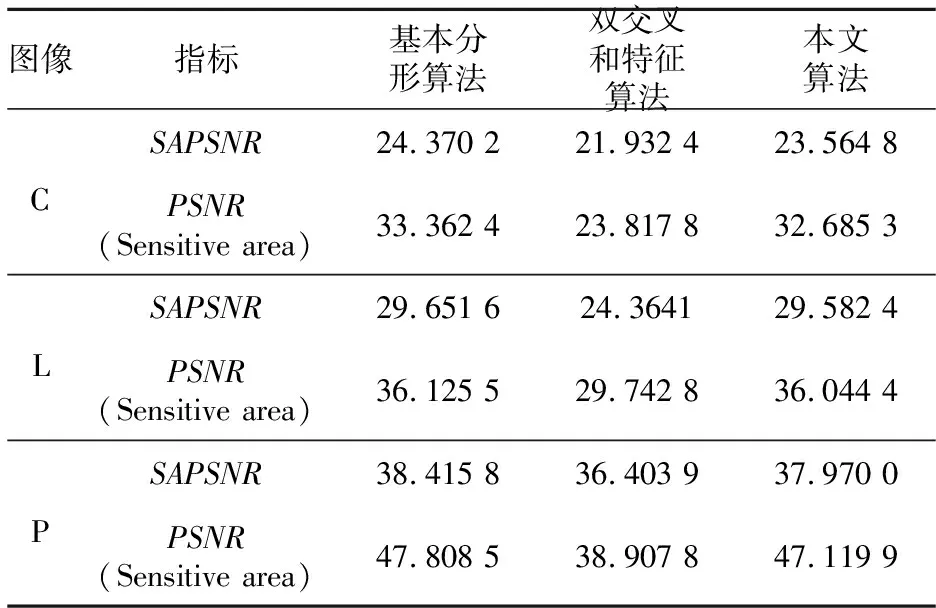
Table 1 PSNR(Sensitive area) and SAPSNR value comparison

如表2所示，實驗中選用的搜索半徑L與R塊長度相同，步長K為R塊長度的10倍，本文算法在PSNR值可以接受情況下，編碼時間相較于基本分形圖像壓縮算法，最高可節省大約64%。

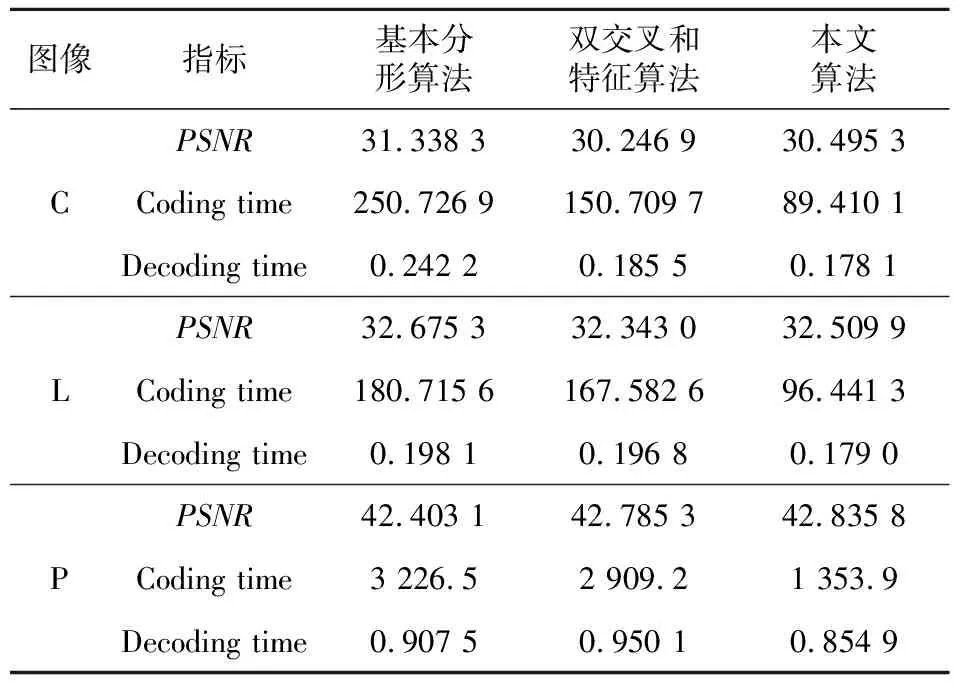
Table 2 Image PSNR,encoding time,decoding time simulation results of C image

分形圖像壓縮算法未劃分敏感區域和重要區域，采用全局搜索方法，從表3中可以看出，CR值與塊大小成反比。雙交叉和算法非敏感區域閾值τ都取4。本文算法中，重要區域內敏感區域劃分閾值取3，非重要區域內敏感區域閾值取4。

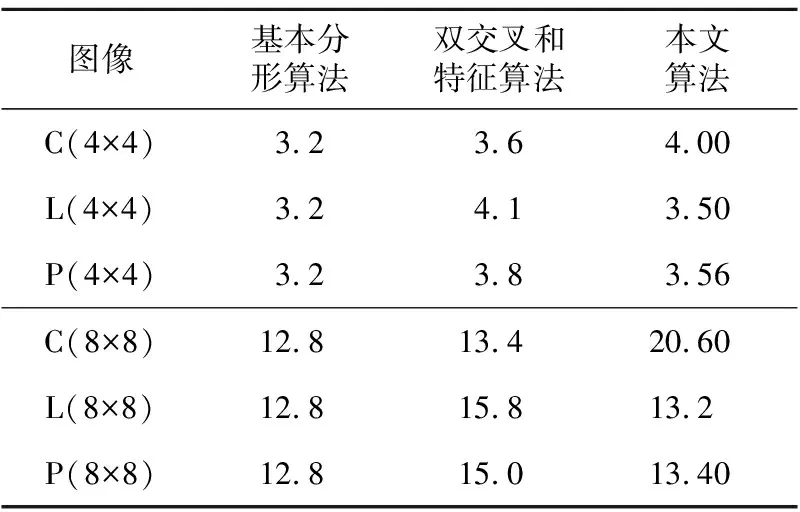
Table 3 Compression ratio of algorithms under different block sizes

圖3是實驗圖像在不同算法以及不同塊大小下的恢復圖像，圖像大小分別為256×256,256×256,512×512,512×512，從左至右分別為原始圖像、基本算法恢復圖像(4×4)、本文算法恢復圖像(4×4)、交叉和算法恢復圖像(4×4)、基本算法恢復圖像(8×8)、本文算法恢復圖像(8×8)。從圖3中可以看出，本文算法恢復的圖像效果比雙交叉和算法恢復的效果更好。

7 結束語

本文提出了一種質心特征和重要敏感區域分類的分形圖像壓縮算法，利用圖像塊質心特征，對相似圖像塊進行近似匹配，在分形圖像壓縮編碼階段，利用質心特征對R塊和D塊進行匹配，有效縮短了編碼階段的時間。同時考慮人眼對圖像敏感區域和重要區域的選擇，采用重要區域和敏感區域劃分方法，增加人眼對恢復圖像效果的好感度。實驗結果表明，質心特征分類和重要敏感區域劃分處理的分形圖像壓縮算法相比傳統算法可以在編碼時間和恢復圖像效果上取得優良效果，同時分類過程中的參數可調整，例如敏感區域劃分閾值、搜索步長和半徑等，具有較強的靈活性和直觀性，具有較好的應用前景。

Figure 3 Recovery results圖3 恢復結果