考慮任務均衡的加油車動態調度問題*

衡紅軍，戚馨桐

(中國民航大學計算機科學與技術學院,天津 300300)

1 引言

車輛調度問題是多項式復雜程度的非確定性問題NP(Non-deterministic Polynomial)，求解該問題通常采用3大類算法，即啟發式算法、仿生算法和精確算法。啟發式算法構造簡單，對于求解較小規模數據較為有效，但對于較大規模數據往往表現欠佳[1 - 3]；仿生算法會因為陷入局部最優的陷阱而無法得到最優解，需要結合其他算法來提高前期搜索能力[4,5]；而精確算法可以獲得問題最優解，卻是以龐大的計算量作為代價的，隨著計算機性能的提升，精確算法運用在大規模調度問題上成為新趨勢[6 - 8]。目前，針對機場特種車輛調度問題的研究較少且以啟發式算法為主，衡紅軍等[9]利用節約值算法歸并回路搜索最短路徑；Wang等[10]提出一種基于貪婪策略的機場加油車調度算法AVSAGS(Airport Vehicle Scheduling Algorithm based on Greedy Strategy)求解該問題。

本文研究機場地面服務中的燃油加注服務。目前，機場地面服務仍停留在人工調度階段，采用單車單服務的方式(即：車輛從車場出發完成1個航班的燃油加注服務后便返回到車場)會使得機場的地面資源利用率降低，同時難以確保加油員工作量均衡。考慮在資源充足時，即當值加油員與加油車為一一匹配關系，加油員駕駛加油車在過站航班和始發航班的進港、出港時段提供燃油加注服務。由于過站航班的到達時刻易受到自然環境、航線流量等因素的影響，導致航班的實際時刻與計劃時刻相差較大，所以采取過站航班在臨近機場時發送的預計到達(進港)時刻以及始發航班的預計出港時刻作為是否為航班安排服務的依據。

基于上述航班時刻特性，本文構建了一種基于動態規劃時間窗的實時車輛調度模型DVRPTW(Dynamic Vehicle Routing Problem with Time Window)[11]，通過航班預計時刻計算航班燃油加注服務時間窗，對服務開始時刻進入到規劃時間窗的航班構建DVRPTW模型，模型根據實際情況加入約束條件與目標函數。之后將動態調度問題轉化為連續時間片下的靜態調度問題[12]。在每個時間片下通過自適應分支定價算法配置車輛、人員為航班服務，車輛根據不同航班的燃油加注服務的開始時刻與結束時刻進行銜接，車輛完成1次任務(服務序列)返回車場。再通過貪婪策略將任務進行銜接，最終實現車輛行駛時間最少，加油員的工作量均衡(差異最小)的目的。

2 問題描述與數學模型

2.1 問題描述

給定N+M個航班集合H={1,2,…,N,N+1,N+2,…,N+M}，其中N表示始發航班的數量，M表示過站航班的數量。集合V={1,2,…,T}表示車輛集合。規劃車輛為航班服務滿足以下約束：(1)每個航班僅被燃油加注服務1次；(2)所有航班僅可在其規定的燃油加注服務時間窗口內被服務；(3)加油員駕駛加油車從車場出發，完成1次任務即返回車場。實現如下目標：(1)車輛行駛時間最短；(2)加油員的工作量均衡。

2.2 數學模型

2.2.1 符號說明

(1)H0=H∪{0},Hn+1=H∪{n+1}，其中0和n+1分別表示將車場視為起點和終點。(2)L為執行燃油加注任務派出的車輛次數。(3)ti,j為航班i所在停機位到航班j所在停機位的車輛行駛時間，其中t0,i和tj,n+1分別表示車輛從車場出發到達i和從j返回車場的時間。(4)xi,j,k表示弧的決策變量，若xi,j,k=1，則表示車輛k服務航班i后，立即對航班j進行服務。(5)ci為航班i的服務時間。(6)si,k表示車輛k為航班i開始服務的時刻。(7)[ai,bi]為航班i的燃油加注服務時間窗，其中ai和bi分別表示服務的最早和最晚開始時間。(8)θ表示不滿足燃油加注服務時間窗的懲罰系數。

2.2.2 DVRPTW的混合整數規劃模型

(1)

(2)

(3)

(4)

(5)

(6)

si,k+ci+ti,j-θ(1-xi,j,k)≤sj,k,

?i,j∈H,?k∈V

(7)

ai≤si,k≤bi,?i∈H,?k∈V

(8)

xi,j,k∈{0,1},?i∈H0,?j∈Hn+1,?k∈V

(9)

其中，式(1)和式(2)為目標函數表達式，分別表示車輛行駛時間最短和車輛之間的任務量差異最小。式(3)～式(9)為約束表式，分別表示：式(3)確保同一航班不被重復執行燃油加注服務；式(4)～式(6)確保加油車從車場出發開始為航班服務，執行完任務后，返回車場；式(7)確保車輛k為航班i服務后，從其所在停機位出發到達航班j所在停機位開始服務并確保開始服務時間在航班j的燃油加注服務時間窗口內，xi,j,k=0時表達式依然成立；式(8)確保所有航班必須在其規定時間窗內得到燃油加注服務；式(9)確保決策變量xi,j,k的取值為0或1。

3 算法設計

3.1 算法設計思想

求解動態規劃問題應該首先將其轉化為多個連續時間片下的靜態調度問題。在每個時間片下，通過自適應分支定價算法規劃車輛的行駛路徑，將航班的燃油加注服務進行銜接形成服務序列，實現車輛行駛時間最短，車輛單次任務的工作量均衡的目的，在此過程中服務的銜接要滿足式(3)～式(9)的約束條件。由于在實際情況中，任務數量往往大于實際車輛數，在保證加油員有休息時間的條件下，通過貪婪策略有效地銜接任務，進一步實現加油員工作量均衡的目的。

3.2 相關定義

定義1動態規劃時間窗(t0+t)，t0表示當前時刻，t表示時間窗的長度。

定義2設k個連續時間片t1,t2,…,tk,每個時間片的長度恒定為Δ，可以得到ti的時間區間為[(i-1)·Δ,i·Δ]。在ti的開始時刻讀取數據，經過τ(τ<<Δ)計算時間生成調度方案，在區間[(i-1)·Δ+τ,i·Δ+τ]執行調度方案。

定義3行駛時間=[行駛距離/行駛速度]。

定義4服務時間=燃油加注時間=[燃油加注量/燃油加注速度]，本文以服務時間作為衡量工作量的尺度。

3.3 工作流程

步驟1初始化預計航班集合、待排航班集合，將當日所有航班標記為“未訪問”。

步驟2在當前時間片ti開始時刻讀取預計航班數據到預計航班集合，若集合不為空，則執行步驟3。

步驟3計算預計航班集合中航班的燃油加注服務窗口，將服務窗口最早開始時刻進入到動態規劃時間窗口且標記為“未訪問”的航班加入到待排航班集合，并將這些航班標記為“已訪問”。

步驟4若當天所有航班都安排完畢，則結束；否則，轉步驟5。

步驟5若待排航班為空，則轉步驟7；否則，轉步驟6。

步驟6通過自適應分支定價算法配置車輛、人員進行燃油加注服務。

步驟7時間片ti開始時刻讀取預計航班數據到預計航班集合，若集合不為空，則執行步驟3。

4 自適應分支定價算法

本文采用動態列生成算法[13]以及分支策略[14]構建一種新穎的自適應分支定價算法。列生成算法通過DW(Dantzig-Wolfe)分解原理[15]將原問題分解為表達式簡單但列變量數目龐大的主問題MP(Master Problem)以及含有資源約束的多目標優化路徑的子問題。由于無法枚舉出主問題的所有列變量，只需得到限制主問題RMP(Restricted Master Problem)，限制主問題的解屬于主問題解的凸子集，即同樣包含最優解。每次迭代將松弛限制主問題模型轉化為其對偶模型，可減少變量基數，加快計算速度。求解對偶模型得到對偶值，重新定價子問題，從而指導列的生成，而對偶模型的檢驗數判斷是否將列加入到限制主問題規模，直到子問題無法產生檢驗數小于0的列，求解RMP即可得到浮點數最優解。最后采取基于弧的分支策略得到整數最優解。自適應分支定價算法流程圖如圖1所示。

Figure 1 Flow chart of branch and pricing algorithm圖1 分支定價算法流程圖

4.1 DW模型分解

4.1.1 符號及表達式

(1)λ1，λ2表示給2個目標分配的不同權重。(2)?={b1,b2,…,bn}表示限制主問題規模中所有列的集合。(3)tr表示當前列r所途經路徑的行駛時間，tr=∑i∈H0∑j∈Hn+1ti,jxi,j。(4)Cr表示當前列r的服務時間，Cr=∑i∈H0∑j∈Hcjxi,j。(5)dck表示列對應車輛k已經完成或正在進行燃油加注服務的航班的總服務時間。(6)若列r包含航班i時ei,r=1，否則ei,r=0，∑i∈H0∑j∈Hxi,j=∑j∈H∑r∈?ej,r。(7)θr表示列的決策變量，解中包含服務序列r時為1，否則為0。(8)C表示每個航班服務序列的目標燃油加注時間，C=∑i∈Hci/L。

4.1.2 限制主問題

將整數線性規劃模型式(1)～式(9)轉化為集合覆蓋模型作為限制主問題模型，再依據4.1.1節的公式推導，可以得到限制主問題模型，定義如下：

(10)

(11)

θr∈{0,1},r∈?

(12)

式(10)與式(1)和式(2)含義一致。式(11)和式(12)分別對應式(3)和式(9)。

4.1.3 資源約束下的多目標優化路徑子問題

松弛后的限制主問題模型的對偶模型定義為：

(13)

(14)

0≤πi≤1,i∈H

(15)

對偶模型的檢驗數為：

(16)

根據等價關系將式(16)細化為基于弧的表達式：

(17)

子問題模型定義為：

(18)

s.t.約束式(3)～式(9)

(19)

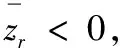
4.2 自適應分支定價算法具體實現

4.2.1 符號說明

(1)W表示等待服務的航班集合，∪s∈?o(s)=W,其中o(s)表示服務序列s所包含的航班。(2)P表示新產生的檢驗數小于0的列的集合。(3)Q=∪k∈Vqk表示車輛覆蓋集合，其中qk表示被車輛k所覆蓋的列集合。

4.2.2 動態列生成算法

算法1動態列生成算法

輸入：待排航班。

輸出：服務序列。

步驟1將待排航班加入到Ni集合。當前時間片ti，若i≥2，轉步驟2；否則,轉步驟7。

步驟2車輛覆蓋集合Q中，若存在集合對應車輛k為空閑狀態，則車輛k返回車場，銷毀屬于qk的所有列。

步驟3刪除所有列中已經完成與正在進行燃油加注的航班，更新W，?，Q。

(1)刪除后，若列不為空，則保持剩余航班相對順序；

(2)刪除后，若列為空且列不屬于Q，則銷毀列。

步驟4單純型算法求解RMP模型，并得到對偶變量πi,i∈W。

步驟5列衍生新列：

(1)插入操作。

①選擇1個列s∈?；

②選擇航班l∈Wo(s)嘗試插入到列s的任何位置，計算o(s)∪l后，o(s)航班服務的花費zs=zsl-πl；

③在列s上重復操作②，直到所有屬于Wo(s)的航班完成操作②；

⑤轉操作①，直到所有列都完成上述操作。

(2)刪除操作。

①選擇1個列w∈?;

②選擇航班l∈o(w),在列w中刪除航班l，計算o(w)l后，o(w)航班服務的花費zwl=zwl+πl;

③在列w上重復操作②，直到所有l∈o(w)的航班服務完成;

⑤轉操作①，直到所有列完成上述操作。

步驟6將P中列加入到?，清空P。

步驟7為Ni中每個航班生成1個新列,將新列加入?。

步驟8重復步驟4與步驟5，直到新生成的列達到基數上限或P為空。

步驟9單純型算法求解RMP模型。

步驟10利用分支策略優化解，若最優整數解中存在不屬于集合Q的列，則根據貪婪策略從車場指定加油車前往服務。

4.3 分支策略

由于將列的決策變量松弛為連續型變量，導致解中多個列包含同一航班。而整數規劃無法解決這一問題，因此采用基于弧的分支策略優化解。假設2個服務序列，r1途徑弧(m,j)訪問j，r2途徑弧(h,j)訪問j。將弧值四舍五入取整，優先選擇弧值變幅最大的弧，假設為弧(h,j)，則會產生2種分支。分支1：保留r2的弧(h,j)，其次將其他途徑j點的傳入、傳出弧的花費設為非常大的值；分支2：將弧(h,j)花費設為非常大。然后重新計算直到求解出最優整數解。下面詳述分支策略的具體過程。

算法2分支策略

輸入：分支節點。

輸出：服務序列。

步驟1初始搜索樹S，加入根節點。

步驟2在搜索樹中選取1個節點s(分支策略)初始化RMP模型。

步驟3求解RMP模型，解為Y。

步驟4若Y為整數解，轉步驟5;否則,轉步驟6。

步驟5將解Y對應的目標值與上界作比較。如果小于上界，則更新上界，并進行剪枝操作；否則，根據上界剪掉當前分支。轉步驟7。

步驟6Y為浮點數解，判斷浮點數解對應的目標值是否小于上界，若小于，則選擇新的分支節點加入搜索樹，刪除當前分支節點；否則，剪掉當前分支。

步驟7如果搜索樹S≠?，轉步驟2；否則,當前整數解即為RMP的最優解。

4.4 貪婪策略

考慮到加油員每次任務間有一定的休息時間，安排給同一加油員的多個任務的窗口不能重疊，而且加油員執行多個任務之間的休息時間不能低于40 min。在滿足上述條件的前提下，每次將新任務指派給累計工作量最少的加油員。

5 實驗及結果分析

為了驗證算法解決實際問題的有效性，本文選取華北某機場的實際數據作為算例，分析并驗證其可行性。

5.1 數據預處理

華北某機場有63個停機位為飛機提供地面服務，機場每天的進、出港航班數量達到300架次左右。根據民航局相關文件規定：機場地面特種車輛的行駛速度不能超過20 km/h，由于機場地下鋪設的油管通道覆蓋所有停機位，因此加油車無需負載燃油即可為航班服務。實驗選取2018年5月23日全天真實航班數據作為實驗算例，共108個離港航班，其中過站航班81個，航班編號101～181；始發航班27個，航班編號201～227。

5.1.1 時序模型預測燃油加注量

在調度規劃時無法得知實際燃油加注量。考慮到航線與燃油加注量的緊密關系，以及相同航線在不同自然環境下對燃油加注量的影響，所以不能單純采用平均值法進行預測，因此本文利用長短時記憶LSTM(Long Short-Term Memory)模型，根據2018年5月23日航班對應航線的歷史數據，預測該日航班的燃油加注量。部分航班的航線的預測燃油加注量如表1所示。

Table 1 Forecasting fuel refueling volume on some routes

5.1.2 停機位的距離鄰接矩陣

航班在指定的停機位等待燃油加注服務。根據測算，2個相鄰停機位的距離大約40 m，車輛在行駛的過程中必須按照指定的路線行駛且線路不存在交叉情況(如圖2所示)。則不同停機位之間的距離鄰接矩陣如表2所示，其中D表示車場。

Figure 2 Ground road map of an airport in north China圖2 華北某機場地面道路圖

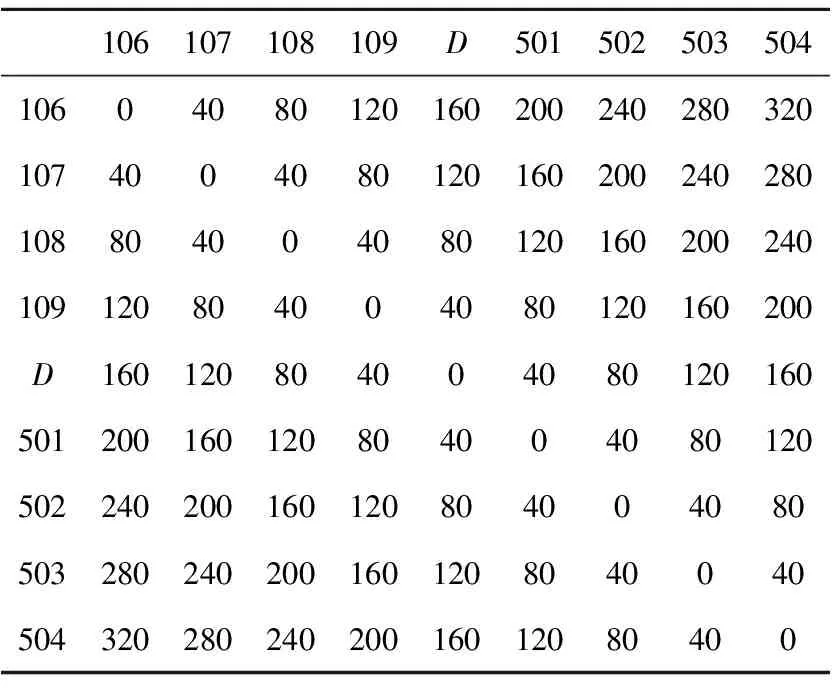
Table 2 Distance adjacency matrix of the stand

5.1.3 航班預計消息

航班消息由民航空中交通管制部門掌控。空管部門會將航班進、出港時刻以報文的形式發給機場。

5.1.4 燃油加注服務的時間窗

燃油加注服務時間窗，表示航班服務可以在航班服務的最早開始時間與航班服務的最晚開始時間的區間內開始，航班服務過早或過晚會導致服務等待或航班延誤，因此航班服務的開始時間必須在其服務時間窗內。計算時將時間類型轉化為十進制類型。

始發航班燃油加注服務時間窗:

bi=td-ci-35

(20)

ai=bi-15

(21)

過站航班燃油加注服務時間窗:

ai=tad

(22)

bi=ai+10

(23)

上式中，td為始發航班預計離港時刻，tad為過站航班預計到達時刻。部分始發、過站航班的服務時間及服務窗口如表3所示。

5.2 結果分析

5.2.1 環境與參數設置

根據本文算法，利用SQL2016對數據進行預處理，CPLEX Optimization Studio (64 bit) 12.6.3學術版對模型進行規范化處理，通過Java編程計算。

Table 3 Service window for some flights

實驗結合實際情況給出以下參數：車輛數為10；車速300 m/min；燃油加注速率300 kg/min；違反燃油加注服務窗口的懲罰系數設為1 000；t設為30 min，Δ設為10 min；系數λ1設置為15，系數λ2設置為10。關于序列目標工作量C的設置：首先由于航班之間的服務時間差極大，設置過小則工作量難以均衡，過大則增加服務銜接進而加大等待時間導致資源浪費；其次已知所有航班總服務時間，為達到均衡目的希望任務次數是加油員數量的整數倍，基于以上2點并通過反復實驗得出C為85。

5.2.2 實驗結果分析

2018年5月23日部分實時航班規劃的結果如表4所示，其中R表示服務序列編號。

Table 4 Partial flight planning results

全天規劃結果以及每個加油員分配的服務序列結果分別如表5和表6所示。

Table 5 Full day flight planning results

2018年5月23日全天航班服務時間2 533 min，平均服務時長為253.3 min，通過式(24)觀測每個加油員服務時間與平均服務時間的差異程度。其中，L表示加油員個數，gi表示第i個加油員的工作量，G表示平均工作量，由計算可知標準差為14.13。

Table 6 Full day flight and fueller planning results

(24)

根據最終的調度結果，可以得到車輛總行駛時間為215 min,所有加油員工作量的標準差為14.13，明顯優于人工調度方式；在相同數學模型下與節約算法對比，自適應分支定價算法在行駛時間、加油員工作量的均衡度與算法的運行時間上同樣具有優勢。如表7所示，其中t,σ,time分別表示車輛行駛時間(min)、加油員工作量標準差、程序運行時間(s)。

Table 7 Comparison results

6 結束語

本文研究了機場航班的燃油加注服務，提出了一種基于動態規劃時間窗的實時車輛調度算法，并通過實例驗證了算法有效性，實現了行駛時間最短，加油員工作量均衡的目的。由于其他機場地面服務同樣依賴于航班的消息，所以對于其他服務(例如客艙清潔、行李運輸等)該算法同樣適用。但是，針對不同數據需要調整動態規劃窗口以及時間片的大小，二者將直接影響調度結果的優劣，同樣影響結果的還有算法計算時間，時間短則可以加快服務部署進程，所以之后工作重點將放在算法的進一步優化上。