一類無約束優化混合共軛梯度法的全局收斂性
翁世有
(蘇州市職業大學 數理部 江蘇 蘇州 215104)
一、引言及參數的算法
針對無約束優化問題

其中:f:Rn→R 是連續可微函數,其梯度函數△f(x)記為g(x)。共扼梯度法的迭代公式如下:
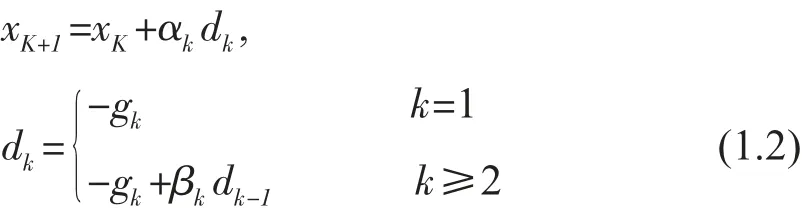
搜索方向要求dk是下降方向的,即

同時,認為搜索方向滿足充分下降條件,當且僅當

目前,有許多不同的共軛梯度[1-2]:
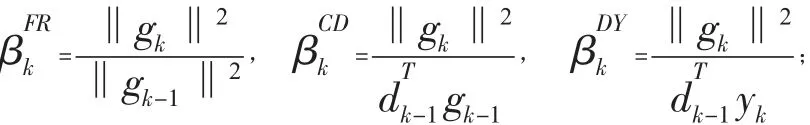
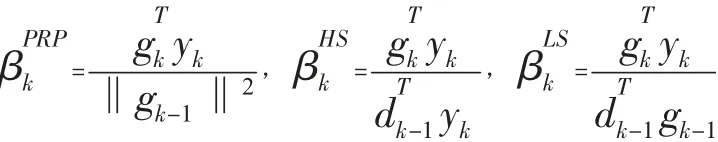
其中,‖·‖為歐幾里得范數,yk=gk-gk-1。
許多學者針對同樣的問題(1),提出不同的共軛梯度公式,進而得到不同的共軛梯度法。Gilbert 和Noceda[3], 張 麗[4]提 出 了 一 類 修 正 的Polak-Ribiere-Polyak (PRP) 共軛梯度法,這個梯度法也滿足了搜索方向dk為充分下降的性質。韋增欣等[5]提出了一個修正的PRP 共軛梯度法,通常稱為Wei-Yao-Liu 共軛梯度法, 滿足了Gilbert 和Nocedal 中的性質。本文基于Gilbert 和Nocedal 的混合CG 參數,提出一類新的共軛梯度法,該方法具有很好的收斂性質和速度。
共軛的一種混合參數[6]有如下形式:
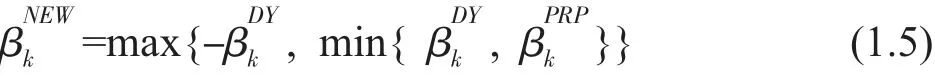
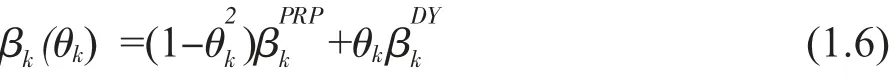
為了使參數βk(θk)更有效,給出一種混合參數θk的計算方法。對于一般的非線性函數,由均值定理可知:存在一個常數ξk∈[0,1] 使得
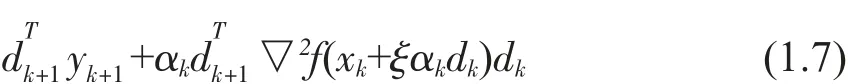
基于該方程和共軛梯度的定義,顯然有下面的等式條件成立:

由共軛梯度方法,βk(θk)作為它的參數如(1.6),根據(1.8)有:
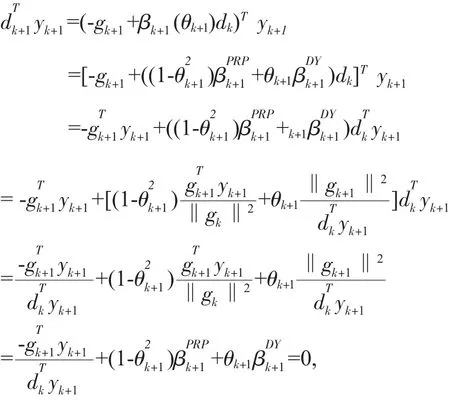
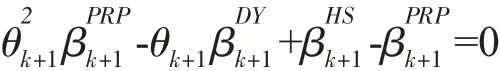
解此方程有得到參數θk:
由此得,混合梯度方法的CG 參數表示為:
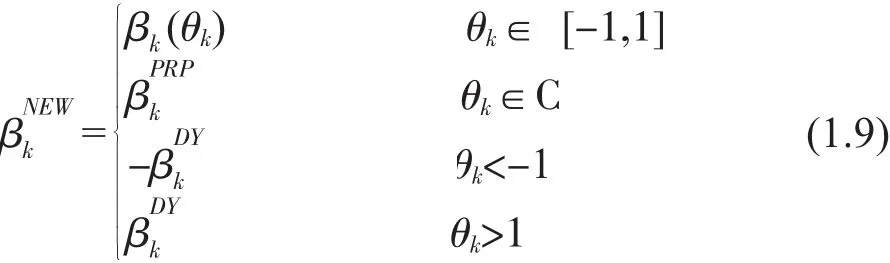
二、全局收斂的證明
Wolfe 線搜索,它要求αk滿足wolfe 搜索準則:
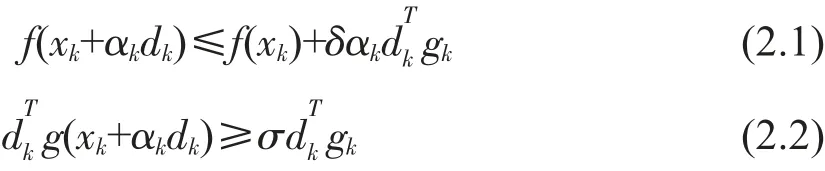
為證明算法全局收斂,需要如下引理:
引理1[7]設目標函數f(x)下方有界,導數△f(x)滿足lipschitz 條件
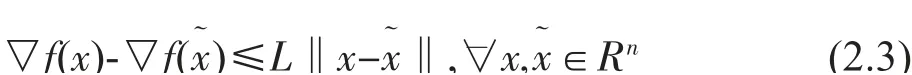
對xk+1=xk+αkdk,其中dk滿足dTkgk<0,步長因子αk滿足wolfe 條件(2.1)和(2.2),則有:

(2.4)通常稱Zoutendijk 條件。
定理1 設目標函數H1:f(x)下方有界;H2:導數滿足lipschitz 條件:
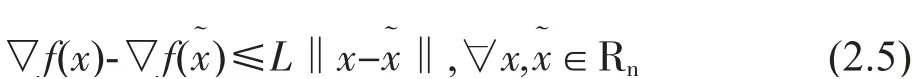
步長因子αk滿足wolfe 條件(2.1)和(2.2),則由(1.9)表出的參數βNEWk使得算法滿足:

證明:利用反證法,若結論不成立,則存在常數ε>0 使得

由
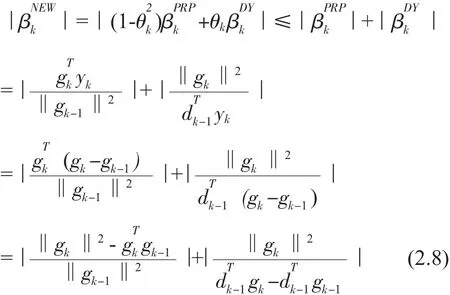
及-gTkgk-1<0,有

由(2.2)
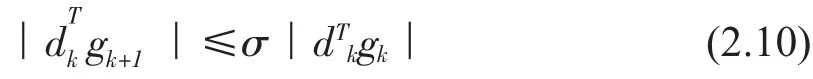

結合dTkgk<-C‖gk‖2有
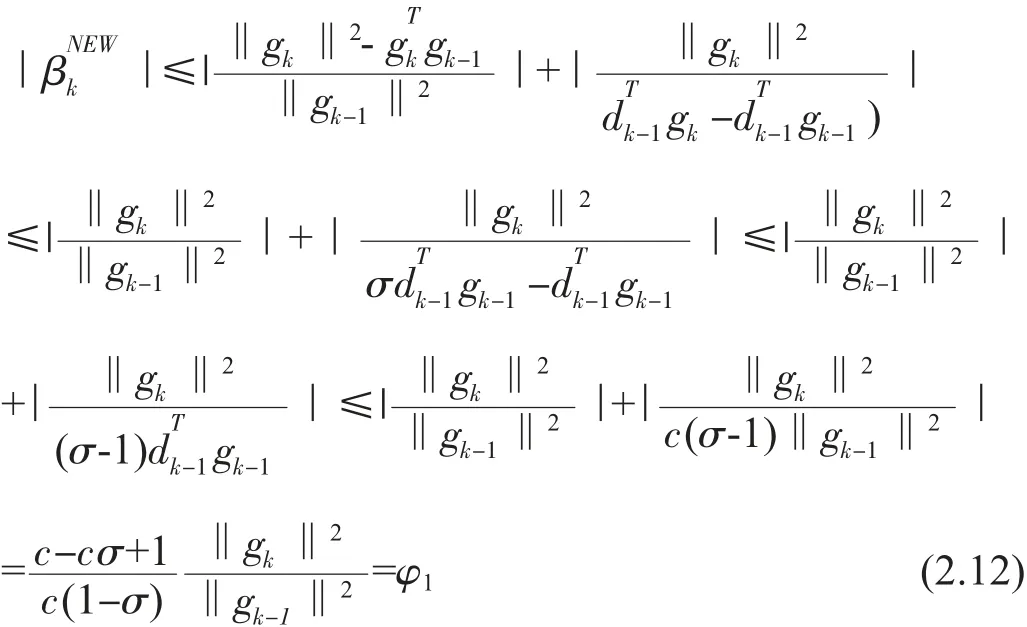
再由
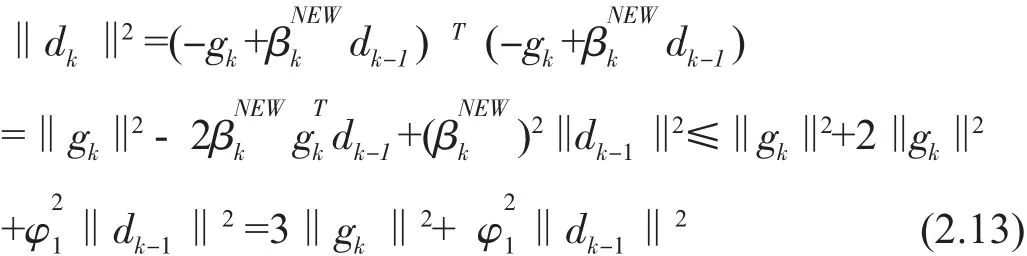
兩端同時除以(gTkdk)2,
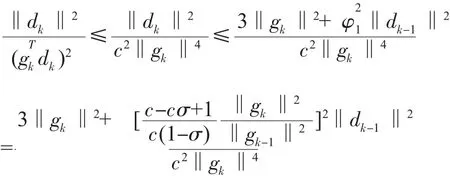
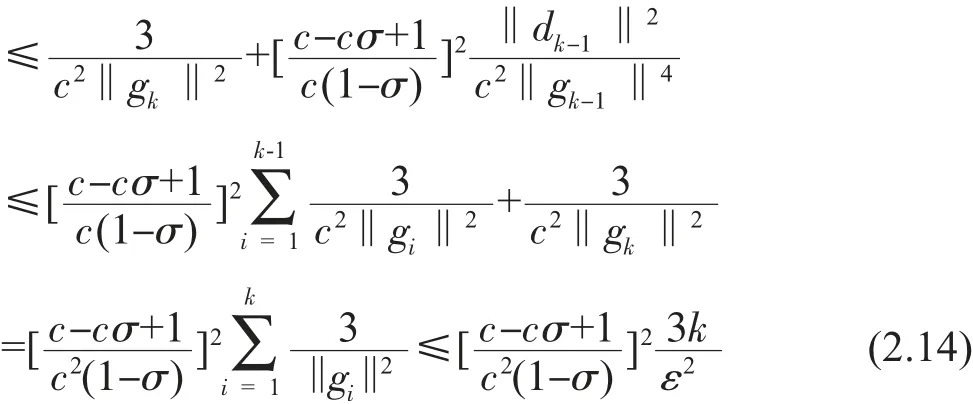
從而

當βk>0時,有

因此
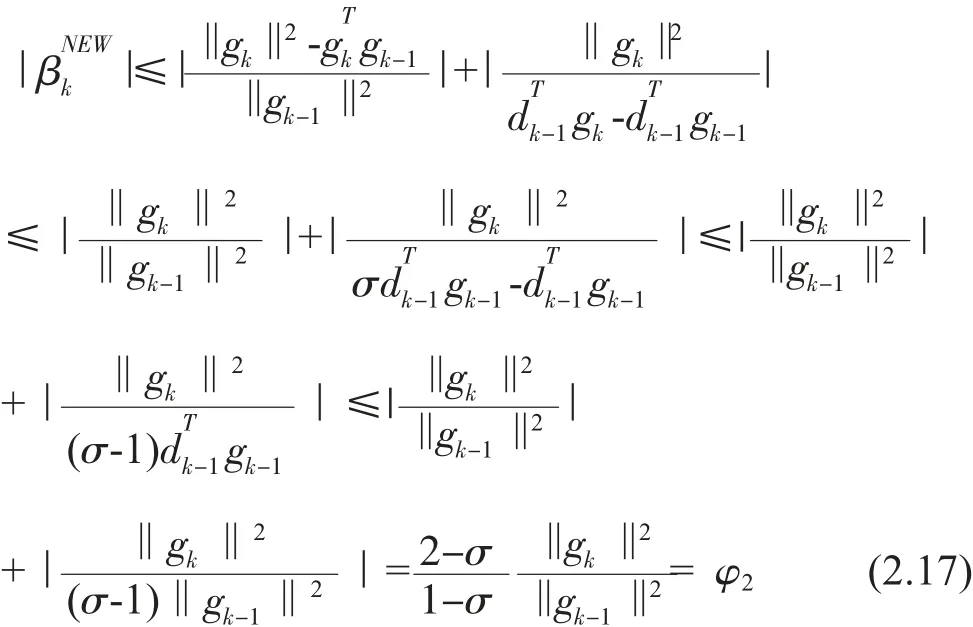
又
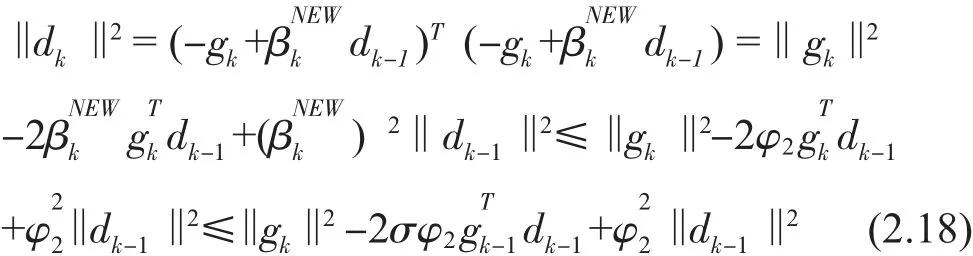
進而
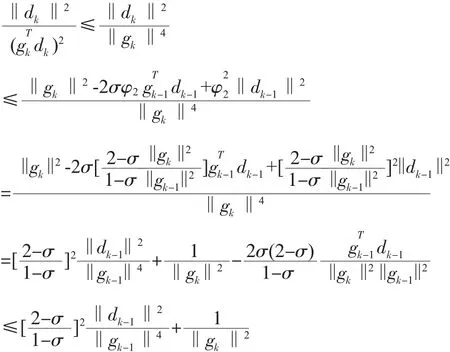
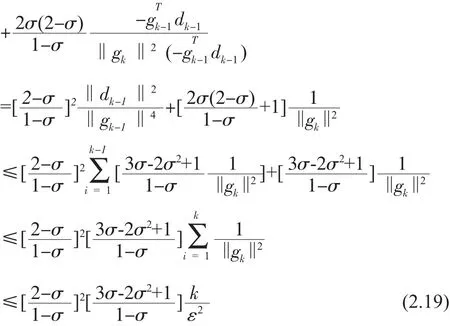
得到,
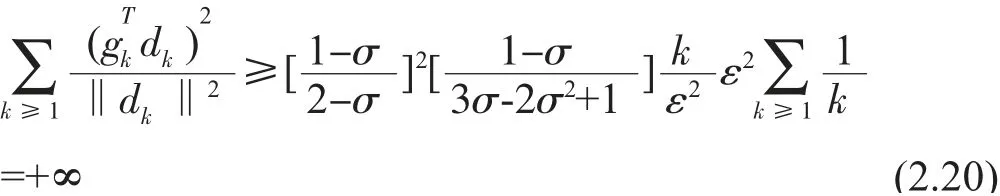
綜上證明,由于(2.15)和(2.20)與Zoutendijk 條件相矛盾,故得證即新參數βNEWk的共軛梯度法在wolfe 條件下全局收斂。
三、數值檢驗
系統環境win7 旗艦版32 位,處理器Intel(R)Pentium(R);CPU G645 @ 2.90GHz;安 裝 內 存4GB。運用MATLAB,實現以下函數的共軛梯度求最小值。詳情函數如下:
統一σ=0.35,δ=0.9,α0=1
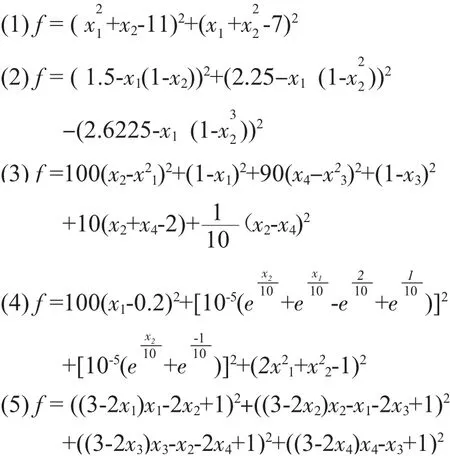
從表1 中5 個函數分別在PRP 參數,DY 參數和新的參數下的共軛梯度法的迭代次數和運行時間可以看出,運行時間相對減少,迭代次數相對降低,由此,本論文提出的混合型非線性共軛梯度法具有良好的計算效果,并且收斂速度快。

表1 各函數在不同參數共軛梯度下的迭代次數和CPUtime

