“數學廣角——推理”教學設計
許華庚 張選勝 楊立高

教學內容:
人教版數學二年級下冊第九單元:“數學廣角——推理”。
教學目標:
知識與技能目標:通過觀察、猜測等活動,讓學生經歷簡單的推理過程,理解邏輯推理的含義,初步獲得一些簡單的推理經驗。能進行含有三個條件的簡單推理。
過程與方法目標:經歷推理判斷的過程,能借助連線法、表格法等方式整理信息,初步培養觀察分析、合理推理的能力,滲透“一一對應”和“轉化”思想。
情感態度與價值觀目標:初步養成樂于思考的良好習慣,感受推理在生活中的廣泛應用。
教學重點:進行有序、全面的思考和分析判斷。
教學難點:能較為清楚地表達自己的思考過程。
教學過程:
一、體驗“一一對應”
1.“動一動”。
師:同學們!在學習新知識之前,我們先來“動一動”,活動活動筋骨,提提精氣神。請大家聽老師的口令:“全體同學!起立—坐下!起立—坐下!起立—坐下!起立—坐下!”
師:女同學!起立—坐下!起立—坐下!起立—坐下!起立—坐下!
師:男同學!起立—坐下!起立—坐下!起立—坐下!起立—坐下!
師:誰能跟老師說說在剛才的“動一動”中,你與你的座椅有什么關系?在活動中你會跑到別人的座椅上去嗎?
生:每個人與自己的座椅都是相互對應的,有對應關系!
2.過渡,引出課題。
師:對!一個人只能對應一個座椅,這種關系就叫作“一一對應”!(教師板書“一一對應”)這節課,我們就用“一一對應”來解決推理中的問題!(板書課題:推理)
設計意圖:通過多種形式的反復地“起立—坐下!”讓學生初步感知“對應”,從而引出“一一對應”,為后面的新授中“一一對應”思想的滲透及應用做好鋪墊。
二、感知兩種情況的推理
1.滲透“連線法”。
活動一:滲透“連線法”。(出示課件)
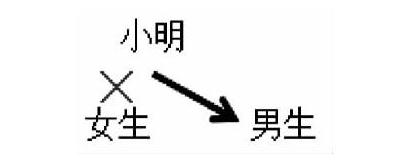
讓思維拐個彎,小明是男生!
要求:創造一種“否定”說法,讓思維拐彎后:小明仍然是男生。
生1:小明還是男生!
生2:小明不是女生!
師:第二個同學的思維拐彎,拐得特別好,你真聰明。依據:我們的性別只有兩種,小明不是女生,就把“女生”排除(打叉),排除了“女生”后,只剩下一種性別“男生”,于是,小明與男生產生一一對應的關系。所以,小明是男生。用連線法表示為(如右圖):
活動二:尋找生活中的“否定”拐彎。(出示課件)
(1)二年級的小雨不是男同學,一定是(女)同學。
(2)小紅的手上分別拿著白球和黑球,她左手拿的是白球,右手拿的一定是黑球。(√)
(3)許老師在教室上課,走的不是后門,一定是(前門)
(4)小麗騎自行車去上街,輪胎壞了,壞的不是前輪,一定是(后輪)。
思考:在一一對應的(兩)種情況下,不是(第一種),就一定是(第二種)。
活動三:用“連線法”創造推理的理由!(出示課件)
有紅、黑兩種金魚游出來,如果最先游出來的不是黑金魚,請問:最先游出來的一定是(? ?)。
2.滲透“填表法”,用“填表法”展示推理的理由!(出示課件)
活動四:一對哥弟雙胞胎,名叫貝貝、樂樂, 樂樂說:“我不是哥哥”,(? ? ? ?)是弟弟。
師:如果把它放到表格里,你又怎樣理解呢?
(學生嘗試后,課件演示“排除法”在填表法中的思維過程)
設計意圖:通過活動引導學生回顧含有兩個條件的推理,為后面學習含有三個條件的推理鋪路搭橋。通過“猜一猜”讓學生充分體驗推理在生活中的廣泛應用,密切數學與生活的聯系。“創造一個理由”目的在于培養學生合理地分析推理能力及語言表達能力。每個活動都先讓學生嘗試自主探究,讓他們經歷困惑、失敗的過程,再來品味成功的喜悅。
3.用“填表法”練習推理的理由。(出示課件)
活動五:有數學和英語兩本書,下面兩人各拿一本。小麗說:“我拿的不是數學書。”小剛拿的是什么書?請填理由:
師:是呀,根據表格,小麗拿的不是數學書,就先把小麗拿的數學書排除(打叉),當排除了數學書后,只剩下英語書,小麗拿的和剩下的英語書就一一對應(打鉤),最終還剩下小剛與數學書,小剛與數學書產生一一對應的關系,所以,小剛拿的是數學書。看來有兩種情況的推理,對于大家來說是沒有被難倒,敢升級挑戰一下三種情況的推理嗎?(出示課本例題1)
三、嘗試“三種情況的推理”
1.嘗試練習。(課件出示例題1)
有語文、數學和英語三本書,下面三人手里各拿一本。小紅說:我拿的是語文書。小麗說:“我拿的不是數學書。”小剛拿的是(? )書,小麗拿的是(? ? )書,請填理由:
師:讀題目,說說你從中獲取了哪些信息?問我們什么?
師:三人各拿一本書是什么意思?(每人拿的書各不相同。)
師:自主探索,用你喜歡的方式在紙上記錄下推理的過程。
學生填表。
2.學生匯報。
根據“小紅拿的是語文書”,所以小紅就與語文書有了一一對應關系,在小紅與語文書處“√”。剩下的小麗和小剛就只能連數學和英語書兩種;再根據小麗拿的不是數學書,在小麗與數學書處排除打“×”,那么英語書和小麗產生一一對應關系,就在小麗于英語書處打“√”,最后剩下的人是小剛,書是數學書,所以,最后剩下的小剛與數學書產生一一對應,就在小剛與數學書出打“√”。
3.教師小結。
師:以上填表法,我們把能夠確定的首先給確定,確定后實際上就排除了一個人(小紅)和一種書(語文書),也就把3種情況的推理轉化為已經學過的幾種情況的推理?
生:兩種情況的推理。
師:然后根據一一對應情況下,兩種情況的推理,不是第一種,就是第二種進行排除與確定的思維進行思考。
設計意圖:本環節由易到難、由淺入深、深入淺出,通過有梯度的練習,鞏固推理方法,提升推理能力!
四、應用“排除法”鞏固新知
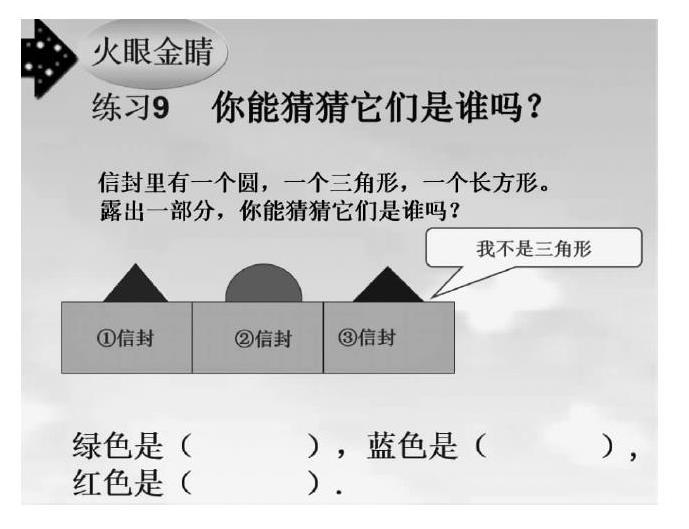
1.砸智慧蛋(如下圖)。
師:根據題意,你認為應該從什么地方入手思考,才能砸開智慧蛋?
生:把能夠確定的首先給確定下來,所以應該先從“女生砸的是3號”去砸智慧蛋。
師:好吧,我們砸開3號智慧蛋看一看是什么?
師:誰起來匯報一下,你是怎樣思考的?
生:三個信封里分別裝著一個圓,一個三角形,一個長方形,圓形最優特點,所以,先把能夠確定的圓形確定了,所以②號信封的綠色是圓形;然后,只剩下一個三角形,一個長方形兩種情況,再根據3號信封說:“我不是三角形”,排除了藍色是三角形,所以3號信封的形狀與長方形對應,藍色就是長方形;最后,只剩下三角形和紅色屬于一一對應的關系,因此,①號信封的紅色是三角形。
師:3號智慧蛋被女生砸了,那么,根據老師砸的不是2號,請問,老師砸的是幾號智慧蛋?
生:老師砸的是1號智慧蛋。
師:為什么?誰起來匯報一下?
生:(略)
師:好!我們1號智慧蛋砸開看一看又會是什么?
師:誰起來連一連?連完線后,說一說你是怎樣想的?
生:在三個案件中,可以首先確定的是26號案件(先連線);然后,只剩下一個6號和16號案件兩個,再根據第一個辦案人員說:“我查的案件號不是最小的”,那么這個人就和16號案件產生一一對應關系(連線);最后,只剩下中間那個辦案人員和6號案件產生一一對應的關系,因此,中間那個辦案人員和6號案件連線。
師:3號智慧蛋被女生砸了,1號智慧蛋被老師砸了,那么,只剩下男生和2號智慧蛋,是誰砸的2號智慧蛋?
生:是男生砸的2號智慧蛋。
師:好!我們來看一看男生砸開2號智慧蛋里又是什么樣的智慧?
學生匯報:(略)
五、課堂小結,概括推理方法
課件:三種情況的推理:首先看是不是一一對應,先把(能確定的確定)后,給予排除,就轉化成為(“兩種”)情況的一一對應。最后想:不是(第一種),就是(第二種)推出結果。
設計意圖:在練習中內化推理方法,滲透中華傳統美德及掃黑除惡的時代信息,開闊學生的視野。
六、拓展延伸
設計意圖:這一環節將難度上升到了有4種情況的推理,將學生的挑戰欲望推到了高峰,可以培養學生舉一反三的能力。也許并非所有同學都能思考出來,但學有余力的同學一定很期待這一餐推理“盛宴”。本環節還將數學與德育相融合,把“核心素養”落實到了課堂中。

