基于核密度估計的泥土物證分類方法

王 黎， 楊瑞琴*， 郭洪玲

(1.中國人民公安大學刑事科學技術學院，北京 100038；2.公安部物證鑒定中心，北京 100038)

泥土物證是一種常見的微量物證，常附著于現場不同物體以及嫌疑人身上。泥土檢驗的目的是提取泥土物證中包含的各類理化信息并由此將嫌疑人與案件及案件現場關聯。對泥土物證的檢驗方法已較為完善，如顏色、粒徑、有機物，元素(包括常量元素、微量元素)、微生物、植物、孢粉等[1]。如果能夠對泥土物證這種復雜體系進行刻畫，將會在案件偵破與庭審階段提供強有力的支持。

元素分析是目前中國泥土物證分析中最常用的分析方法[2]，該方法選取特定元素進行元素含量的測定，依次比較各種元素含量是否有顯著差異。城市泥土樣本元素含量分布是城市樣本間比對的基礎，前人的研究主要集中泥土元素含量的基礎上，對于該物證的比對問題只能給出經驗性的判斷，缺乏相似度計算的數理統計方法，即沒有建立泥土物證比對的標準[3-4]。

為給出泥土物證間的相似度大小，引入了核密度估計與似然比檢驗。在進行泥土元素檢驗時需要對該元素的樣本分布進行估計，通常采用正態分布來擬合。但實驗數據表明，僅有部分地區或者部分元素的數據結果符合正態分布，這時一些基于正態分布的假設檢驗方法將不再適用。首先針對這一問題引入核密度估計，對泥土元素數據的分布統一進行估計，選用高斯核函數并確定最佳窗寬，得到元素分布的概率密度函數。其次利用判別分析對泥土物證進行分類。判別分析在法庭科學領域的應用已較為成熟[5-6]，但判別分析需要樣本滿足正態分布，因此引入核密度估計-似然比檢驗的方法可以在估算樣本總體分布的基礎上計算樣本間的相似度，通過LR(likelihood ratio)的大小判斷給出兩樣本相似假設的支持力度。

1 實驗方法

1.1 泥土樣本采集

在城市各個區縣選取采樣點。在選取采樣點時，避開渣土，建筑垃圾，道路等受外來土或其他流動因素干擾較大的區域。在每個采樣點以五點取樣法，在每個點位鏟去表層土、植被、腐殖質等，在2～3 cm深取約500 g土樣，將五份樣本混合均勻后裝袋封存并標號。

1.2 樣品前處理

烘干：將采集到的每一份樣本裝滿培養皿(濕重約200 g)，放在烘干箱以105 ℃條件烘干120 min。烘干后的樣本需用紙質袋(紙質物證袋)封存，并將其置于干燥箱或者有干燥劑(無水硅膠)的干燥皿中保存且盡快進行后續處理。

研磨：先用20目分樣篩將碎石、植物殘渣、動物尸體(蚯蚓、昆蟲等)等篩除。初篩樣本采用球磨儀研磨，取烘干后的樣本約50 g置于經酒精棉洗凈的瑪瑙桶中，并加入約20顆直徑8 mm的瑪瑙球，反復試驗后將研磨程序設置為15 min，450 r/min。研磨后要確保樣品全部通過200目分樣篩。

1.3 樣品制備與儀器分析

實驗采用X射線熒光法在膠圈模具(內徑3 cm)內裝入足量已研磨泥土樣本，置于壓片機在20 MPa壓強下壓片3 min，將其制成厚約2 mm的薄片，放入X射線熒光儀(ZSX100e)分析[7]，采用XRF內標法，以X元素為內標，測定Al、Si、Fe、K、Na、Mg、Ca、P、Mn、Ti相對百分含量。

2 數據分析

2.1 統計方法原理與方法

2.1.1 KS(Kolmogorov-Smirnov)檢驗

KS檢驗，基于累積頻率分布，用于檢驗該樣本分布是否符合某種理論分布。它假設兩者無顯著性差異，利用樣本累積頻率分布與理論分布的偏離值，來檢驗樣本分布與理論分布是否匹配。當KS統計量顯著性水平大于臨界值P=0.05時，認為該樣本符合理論分布。采用KS檢驗泥土樣本元素含量是否符合正態分布。

2.1.2 核密度估計與最佳窗寬

核密度估計(kernel density estimation，KDE)是一種估計樣本總體概率密度函數的非參數估計方法,在運用核密度方法估計元素分布的概率密度函數時，重點在于核函數K(x)的選取和窗寬h的確定。常用核函數有均勻核、三角核、二次核、四次核、高斯核、余弦核，采用高斯核函數。在窗寬的選擇過程中指標積分均方誤差(mean integrated squared error，MISE)，MISE是核密度估計中常用的評價標準，其計算公式為

(1)

(2)

(3)

式(3)中：E為求期望運算。其中f(x)2不受核函數K(x)選擇的影響，則可以定義代價函數Cn(h)：

(4)

(5)

其中，ψh(ti,tj)為與樣本ti,tj有關的積分變量，公式為

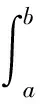
(6)

可以利用式(6)編程計算最佳窗寬值。

2.1.3 判別分析

判別分析是一種在一些已知研究對象用某種方法已經分成若干類的情況下，確定新的樣品的觀測數據屬于哪一類的統計分析方法。常見的有距離判別、Fisher判別(又稱線性判別分析，linear discriminant analysis，LDA)和貝葉斯判別。在法庭科學領域是常用的分類分析手段。采用Fisher判別法對實驗數據進行分類分析。

2.1.4 似然比檢驗

似然比檢驗是一種反映樣本靈敏度與稀有度的復合指標，是貝葉斯分析的一種特殊情況。在微量物證領域似然比檢驗的應用就是以零假設與備擇假設之比的大小來衡量物證的價值，即實驗結果E的條件下假設H1：源于同一客體的概率P(E|H1)與假設H2：源自不同客體的概率P(E|H2)大小的比值，即：

LR=P(E|H1)/P(E|H2)

(7)

為了讓LR更直觀地為調查人員接受，Evett等[14]提出了一種LR的習慣性表述(表1)。

表1 LR所代表的含義Table 1 The implication of the LR

采用Zadora等[15]提出的LR計算方法，在對h取值改進的基礎上計算LR，從而對樣本間相似度大小進行度量。

2.2 數據正態性檢驗

實驗結果為福州(N=50)與呼和浩特(N=50)兩地十種元素相對百分含量數據，由于各元素區間差異較大，因而統一對數據做對數變換。將轉換后的數據進行KS正態性檢驗(IBM SPSS Statistics 20)，檢驗結果如表2所示。結果表明只有少部分元素含量分布符合正態分布(Sig>0.05)，因此采用核密度估計統一對元素含量分布進行估計，其中Mn元素數據波動極小(標準差σ=0.045 465，變異系數CV=-2.772%)，擬合已無意義，不納入后續數據處理過程。

2.3 最佳窗寬算法實現

表2 福州、呼和浩特泥土元素含量正態性檢驗結果Table 2 Results of normality test of soil elements in Fuzhou and Hohhot

注：*表示真實顯著水平的下限；a表示Lilliefors 顯著水平修正。

(2)編輯函數：

function(c)=Cn(h,t)

(8)

(3)調用(2)中函數，由小到大代入h，找到使得函數值最小的h，同時可做出函數Cn(h,t) 隨窗寬h變化的趨勢圖(圖1)。

圖1 窗寬h的代價函數(以福州市P元素為例)Fig.1 The cost function of the bandwidth h (take the Fuzhou P element as an example)

圖2 福州市P元素最佳窗寬示意Fig.2 The best bandwidth for Fuzhou P element

以福州市P元素數據為例。經上述算法可得h*=0.017[Cn(h)min=-1.155]，并按h*做出P元素概率密度函數(Rversion 3.5.2)。在圖2中，在大于最佳窗寬h*處作圖存在過擬合的情況，而在小于最佳窗寬處密度函數平滑性較差，圖2(c)得到了最小代價函數條件下福州市泥土樣本P元素含量分布。事實上，可以對所有元素樣本總體分布統一采用KDE過程進行概率密度函數估計，便于后續分析，如表3所示。采用計算出的最佳窗寬可以得到元素分布的概率密度函數。得到的元素分布概率密度函數可以代入元素分類與比對的似然比模型，計算出樣本間似然比值的大小作為分類與比對的依據。

表3 兩地元素分布最佳窗寬Table 3 The best bandwidth of the element distribution between the two places

2.4 樣本分類

2.4.1 判別分析

對福州市和呼和浩特市兩地泥土樣本進行費歇爾判別分析(IBM SPSS Statistics 20)，如圖3所示，判別結果表明兩地泥土樣本在市級層面有著良好的分類效果，數據總體分為了福州市與呼和浩特市兩類，但在對市區間樣本分類時效果不理想，判別率與回判率也較低(回判率63%，交叉驗證正確率42%)。為對市區間樣本進行合理分類，采用似然比檢驗計算樣本間相似度大小。

圖3 福州市與呼和浩特市泥土樣本判別分析散點圖Fig.3 Scatter plot of the discriminant analysis of soil samples in Fuzhou and Hohhot

2.4.2 似然比檢驗

將核密度估計得到的最佳窗寬h*取均值(h*=0.058 89) 后代入似然比檢驗，計算各市區樣本間的LR，結果如表4所示。可以看到在市級層面比較，LR極小(表4左下部分)，可以近似為0，即兩市樣本間存在較大差異。在區級層面比較，LR值大小不一(表4左上與右下部分)，倉山區與臺江區間LR(LR=3 704)較大，即對兩區域樣本相似的假設有著強烈支持；而回民區與賽罕區2號間的LR(LR=0.000 041 04)較小，即兩區域樣本差異較大。由此，表2所示矩陣可以清晰地給出區域間樣本相似度的大小，直觀判斷兩區域泥土樣本是否相似，可作為判別分析的補充。

表4 福州、呼和浩特泥土樣本區域間LRTable 4 LR between the soil samples of Fuzhou and Hohhot

注：上標1、2表示20個樣本分別在呼和浩特市賽罕區的兩個區域采集。

3 結論

在核密度估計過程中采用最小MISE準則，使擬合出的概率密度函數盡可能接近原始樣本總體，是估計未知樣本分布的可靠的方法。研究結果為不符合正態分布的樣本總體提供了建立數據模型的手段，為泥土樣本元素含量數據的概率密度函數估計建立了統一的方法。同時，針對不同層級的分類需求，初步利用判別分析與似然比檢驗建立泥土樣本分類的方法。