關于機械能守恒定律是否滿足相對性原理的探討

楊習志 趙 堅

(1. 昆明市第一中學，云南 昆明 650031； 2. 昆明市五華區基礎教育科學研究中心，云南 昆明 650031)

筆者發現關于機械能守恒定律是否滿足相對性原理的爭論，[1～7]其核心問題主要來自于3個方面.其一，討論問題中系統的機械能作為物理量所涉及的守恒是否滿足相對性原理，是否是協變的？其二，機械能守恒定律作為一條物理定律是否滿足相對性原理，是否是協變的？其三，系統的機械能不具有獨立協變性是否與相對性原理矛盾？為此，筆者分別從這3個角度出發進行探討.

1 系統的機械能是守恒量嗎？

在分析力學里，對于力學量

w=w(qα,pα,t).

判斷其守恒的充要條件是

其中qα、pα、t為力學量w的廣義坐標、廣義動量和時間，

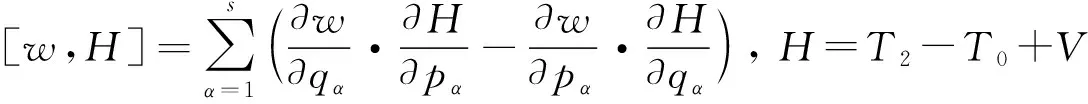
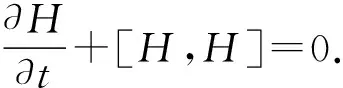
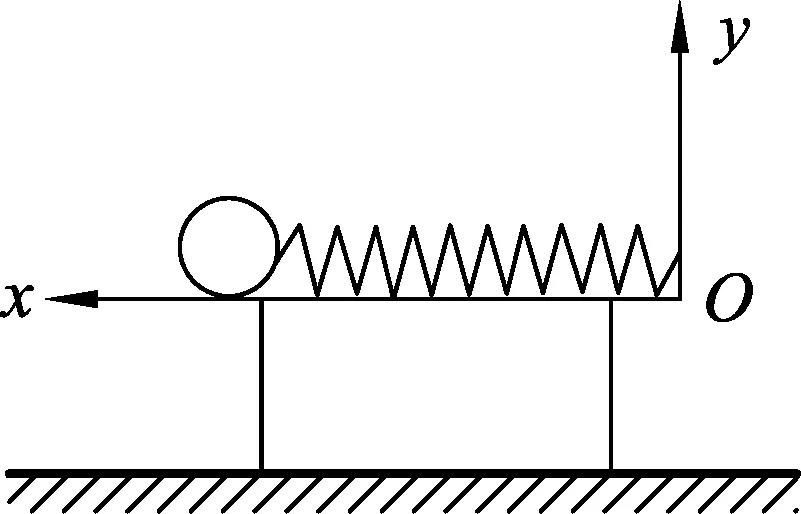
圖1

如圖1所示，在光滑的水平桌面上有一個質量為m的小球與一根輕質彈簧連接，彈簧的右端固定在O點，勁度系數為k,原長為x0,則小球與彈簧整個系統廣義能量的哈密頓量：

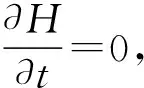
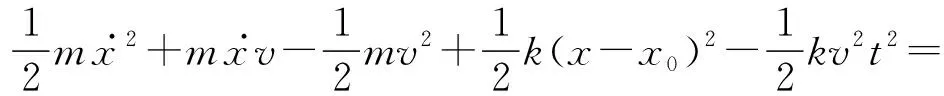
從式中可以看出經過坐標變換后的哈密頓量H′是顯含時間的,即

故變換后系統的機械能不守恒．同理,若在y方向上運動的慣性參考系來進行觀測,經過坐標變換后,會發現變換后系統的機械能仍然守恒,可見系統的機械能不是一個普遍的守恒量,它會隨參考系的改變而改變．究其原因,通過前面的討論會發現主要是因為機械能的哈密頓量中勢能V是位置的函數,而位置坐標在進行該方向上的坐標變換時會攜帶時間,導致機械能的哈密頓量H對時間的偏導數不為0．同理可得系統動量的哈密頓量與位置坐標無關,在經過坐標變換后的哈密頓量仍然不顯含時間,故系統的動量是一個守恒量．

我們也可從機械能守恒的條件出發來進一步分析.根據功能原理,機械能守恒的條件是外力與內非保守力做功為0,其中內力做功

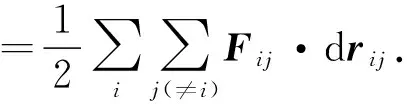
根據坐標變換有

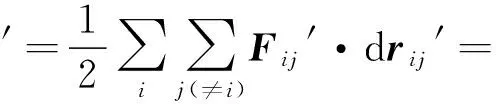
故內力做功與參考系無關,其中內力又分為保守內力和非保守內力,保守內力做功等于系統相互作用的勢能的減少量,非保守內力則會改變系統的機械能,如摩擦生熱或爆炸．

對于外力做功

dw外=∑Fi·dri.

根據坐標變換有

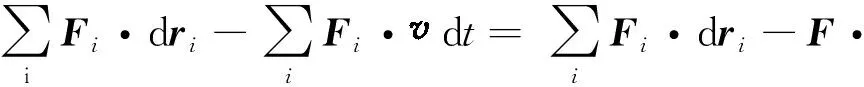
可見,由于外力做功與參考系有關,不滿足協變性,從而導致機械能守恒的條件在經過坐標變換后得不到滿足．故系統的機械能作為物理量而言是不滿足協變性的,它不是一個守恒量．反觀動量守恒問題,由于系統動量守恒的條件是合外力為零,而合外力是不會隨慣性參考系的選取而變的,即在一個慣性參考系中系統所受的合外力為零,那么在另一個慣性參考系中系統所受到的合外力仍然為0,故系統動量守恒的條件滿足協變性,系統的動量是一個守恒量．

2 系統的機械能不具有獨立協變性是否與相對性原理矛盾?

2.1 相對性原理表述之聯立協變

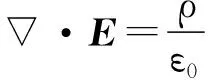
2.2 機械能守恒定律與協變集

如果自然界若干定律聯立在一起,進行參考系變換,然后再在新參考系中對變換結果進行等價變形,可化為具有原來形式的全部新定律,則這些定律稱為是聯立協變的.這些定律作為元素所構成的集合稱為協變集,其中,只含有一個元素的協變集稱為單元素協變集,元素不能再減少的協變集稱為最小協變集．如麥克斯韋方程組中的高斯定理與修正的安培定律,法拉第電磁感應定律與高斯磁定律分別構成兩個四元素最小協變集,電荷守恒定律構成單元素最小協變集,機械能守恒定律則屬于功能原理的最小協變集．

3 機械能守恒與功能原理聯立協變

功能原理即

dw=dw內+dw外=dw內保+dw內非保+dw外保+dw外非保=-(dEp內+dEp外)+dw內非保+dw外非保=-dEp+dw非保=dEk.

dw非保=dEp+dEk，

當dw非保=0時,dEp+dEk=0，

即Ep+Ek=C.

故機械能守恒是功能原理的特殊情況,但由于條件dw非保=dw內非保+dw外非保中的dw外非保與參考系有關,故機械能守恒的條件是與參考系的選取有關的．值得注意的是,根據坐標變換有

dw外′=dw外-F·udt，

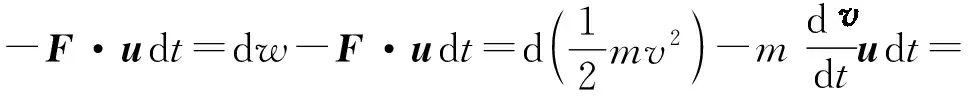
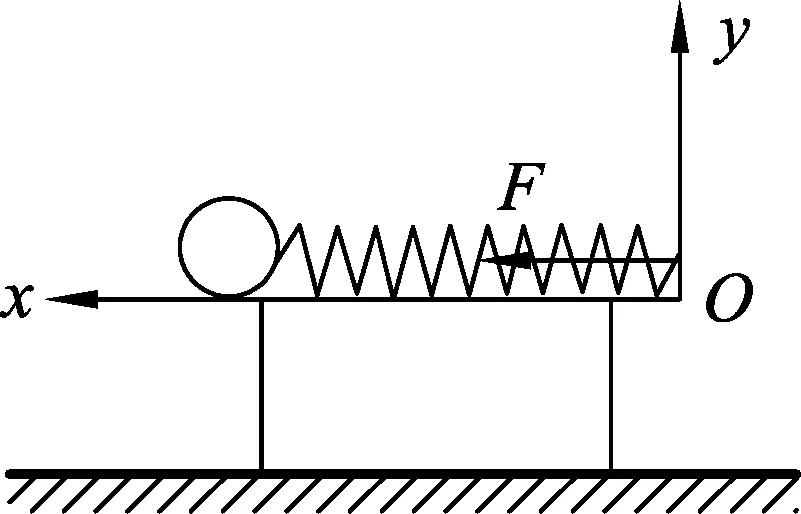
圖2

可見功能原理滿足相對性原理,是協變的．其次,由于機械能守恒是功能原理的特殊情況,故機械能守恒是功能原理的最小協變集,與功能原理聯立協變．下面從功能原理出發,重新探討在x方向上以u向右運動的慣性參考系中來觀測圖1中系統的機械能,假設彈簧此時處于壓縮狀態,且小球正在向右運動,則小球和彈簧整個系統將受到墻壁對它向左的推力F的作用,故有

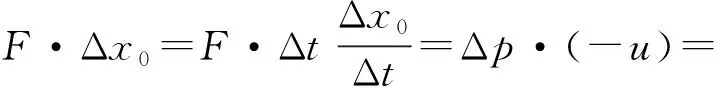
-mu(v2-v1).

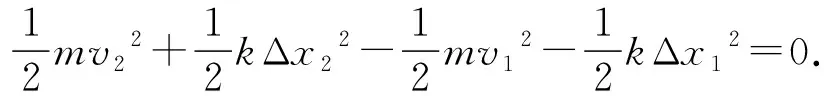
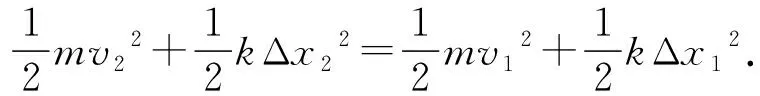
可見,從功能原理出發,可以得出與地面為參考系下相同的機械能的表達形式,因此,機械能守恒與功能原理是聯立協變的．

4 守恒量與守恒定律

鑒于此,我們可以這樣認為,機械能守恒定律是能的守恒和轉化定律(功能原理)在力學中的一種特例．作為自然界最普遍的物理規律之一的能的守恒和轉化定律,一定是滿足相對性原理,是協變性的,但是加上一些不協變的條件(初始條件、邊界條件、規范條件等),就不協變了,因為,能量守恒定律的普遍表述是“一個系統能量的變化等于非保守外力做功”.這句話不能理解為“能量不變(守恒)”,能量不變(守恒)涉及3個問題: (1) 系統的選擇,(2) 什么是保守力?(3) 做功的條件,而我們只有對選定的系統才能區分內力和外力．我們通常說保守力做功與路徑無關,是指沿路徑的積分是“等時”的,沒有移動時間的概念,同時,保守力一定是個勢力場,而只有不含時間的力場才能保證能量不變,否則能量必然變化．所以,一切普遍規律(微分方程)都是協變的,此點無容置疑,可是,系統的機械能守恒在滿足相對性原理,是否具備單獨協變性的問題上,是有條件的,它只能與功能原理聯立協變．

綜上所述可以看出,機械能守恒定律作為物理定律在守恒條件滿足的情況下在任意慣性系下均具有相同的表達形式,滿足相對性原理,是協變性的．但系統的機械能作為物理量來說本身并不是一個守恒量,其根本原因在于機械能的哈密頓量中勢能是位置坐標的函數,在進行該位置坐標上的坐標變換時總會攜帶時間,導致其哈密頓量對時間的偏導數不為0,也可理解為外力做功與參考系有關導致機械能守恒的條件隨參考系的選取而變,使得系統的機械能不滿足相關坐標變換,此時,系統的機械能只能與功能原理聯立協變．

(致謝:本文曾得到北京大學趙凱華先生的悉心指導,借此深表感謝!)