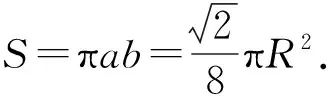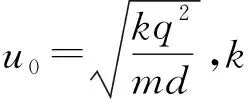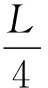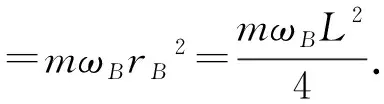有效勢能在高中物理競賽中的應用

胡少希 孫 偉

(1. 南京市玄武區教師發展中心,江蘇 南京 210016; 2. 江蘇省泗陽中學,江蘇 泗陽 223700)

在有心力作用下質點的運動是比較常見的運動,這類問題在競賽考題中出現的頻率很高,質點的有心力問題用力心為極點的極坐標系描述較為適宜.在極坐標系中物體的機械能滿足

(1)

有心力作用下質點角動量守恒

L=mrvθ.

(2)

聯立(1)、(2)式得

(3)

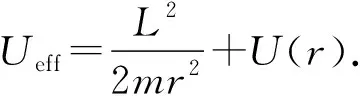
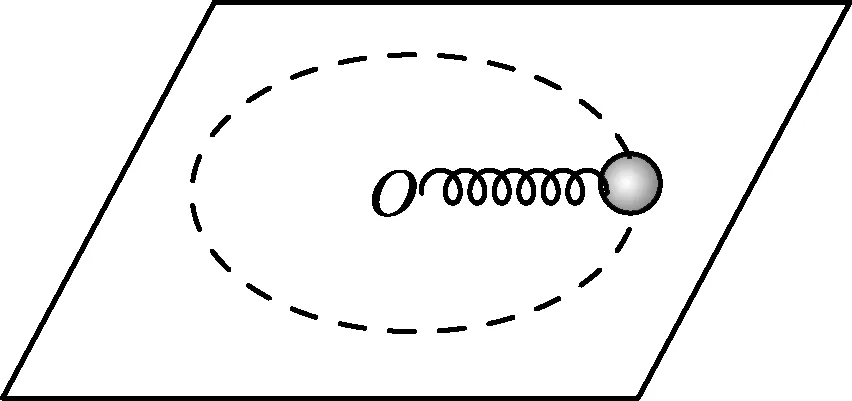
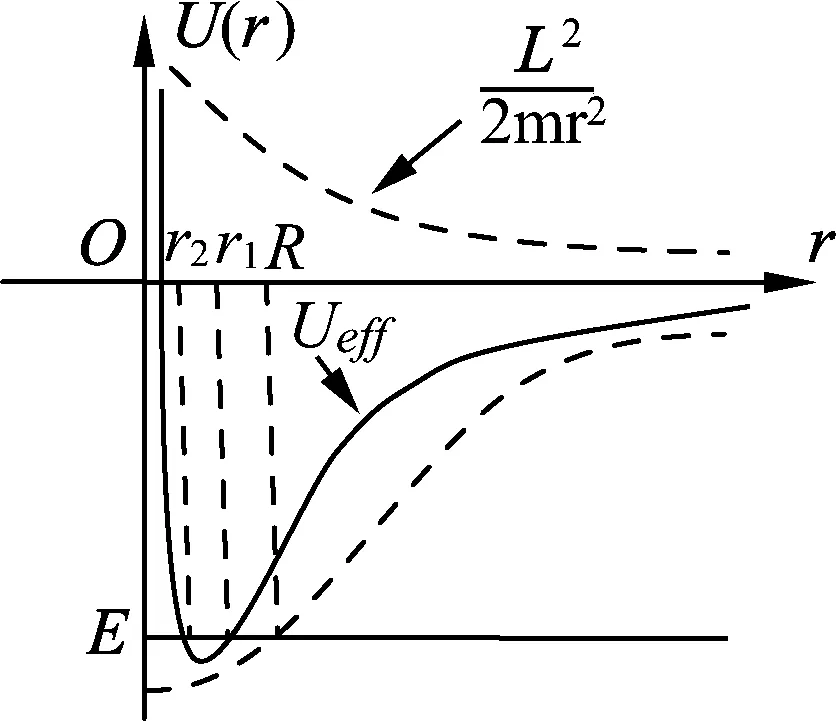
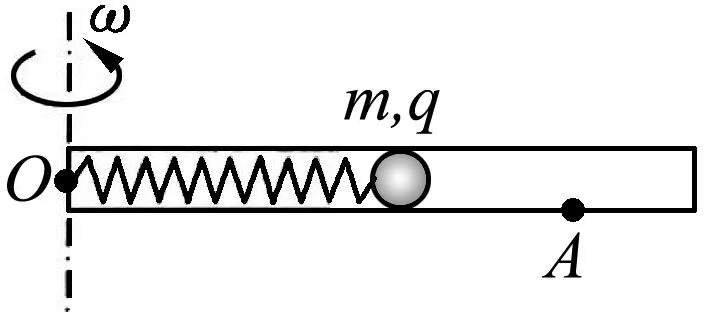
圖1

例1.(國家集訓隊)如圖1所示,在光滑的水平面上,一個勁度系數為k=3.0 N/m的輕彈簧一端固定于O點,另一端拴接一個質量為m=2.0 kg的小球,假設彈簧在無力作用時沒有原長.若小球在彈簧作用下作勻速圓周運動,系統總機械能為E=12 J,現沿小球運動的徑向給其突如打擊,使小球瞬間獲得一徑向速度vr0=1 m/s,求此后運動過程中小球距O點的最近距離和最遠距離.

解析:設小球受打擊前運動的速度為v0,軌道半徑為r0,則

(1)

(2)

聯立(1)、(2)式得

(3)

小球受打擊后系統能量為

(4)

代入數據得

E′=13 J.

(5)

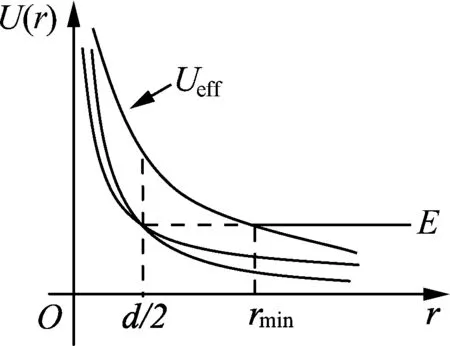
有效勢能為

(6)

由于徑向打擊不影響小球的角動量,故小球角動量守恒,即

L=mv0r0.

(7)

聯立(6)、(7)式代入數據得

(8)

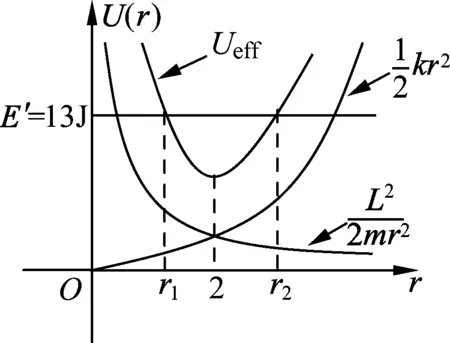
圖2

作出有效勢能圖線,如圖2所示.小球的徑向運動滿足E′≥Ueff,結合圖2可知小球的徑向運動范圍在r1與r2之間,當E′=Ueff時,聯立(5)(8)式得

(9)

由(9)式得

r1=1.63 m，r2=2.45 m.

(10)

分別為小球運動過程中距O點的最近距離和最遠距離.

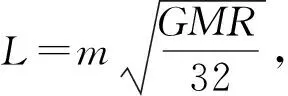
(1) 試問此子彈的運動是總在云里?總在云外?還是有時在云里,有時在云外?

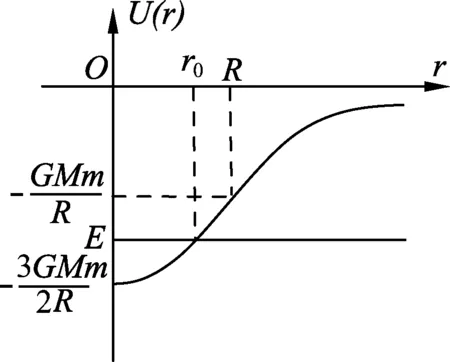
圖3

(2) 求子彈運動軌道的轉折點離氣體云中心的距離;

(3) 討論子彈運動軌道的形狀,并求其運動周期.

解析: (1) 在r≤R區域,子彈受到氣體云團的萬有引力大小為

(1)

在r>R區域,子彈受到氣體云團的萬有引力大小為

(2)

選擇無窮遠為引力勢能零點,則在r≤R區域,引力勢能

(3)

則在r>R區域,引力勢能

(4)

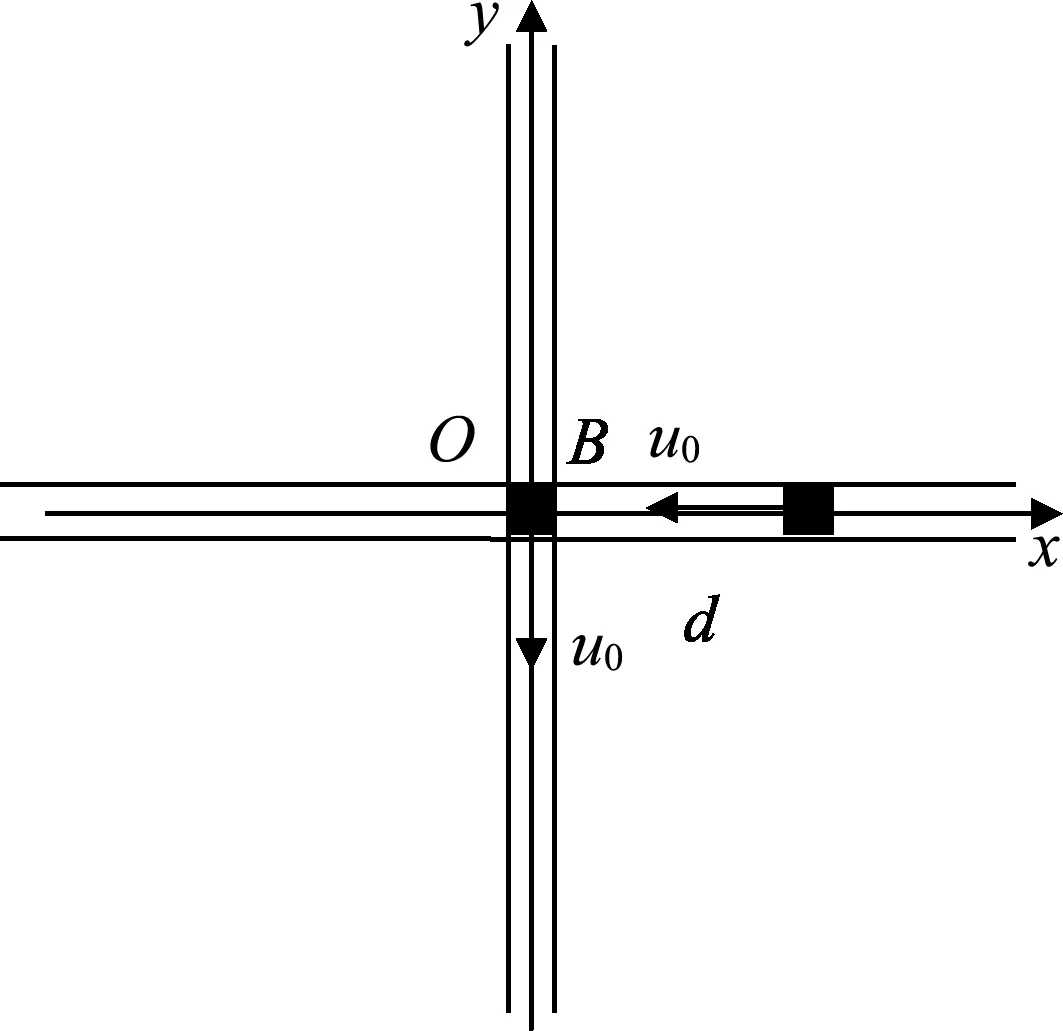
作出勢能圖線如圖3所示,子彈能出現的區域應滿足E≥U.由圖3知,只有在r≤r0區域子彈才可能出現,而r0

(2) 子彈的有效勢能

(5)

圖4

作出有效勢能圖線,如圖4所示.軌道轉折處滿足

E=Ueff.

(6)

聯立(5)、(6)式得

(7)

解得

(8)

(3) 根據以上討論可知,子彈的機械能與有效勢能曲線有兩個交點,因此子彈運動為橢圓軌道,其半長軸和半短軸分別為

(9)

(10)

子彈相對氣體云中心角動量守恒,可知其面積速率k為恒量,其滿足

(11)

故子彈軌道運動的周期

(12)

圖5

解析:分析某時刻質點A和B受力知，

質點A:

Fsinθ=NA.

(1)

質點B:

Fsinθ=maB.

(2)

圖6

以質點B為參考系,質點A還受到大小為maB的慣性力,如圖6所示.由(1)(2)式知:此慣性力正好與彈力NA平衡.也就是說,以B為參考系,A相當于在有心力場中運動.設A、B間距離為r,則A的有效勢能為

(3)

其中A相對B的角動量

(4)

把(4)式代入(3)式得

(5)

A相對B的能量

(6)

圖7

畫出有效勢能圖線如圖7所示,E≥Ueff是可能的運動區域,二者距離最近時滿足

E=Ueff.

(7)

圖8

(1) 彈簧系數k0及小球在B處時細管的轉速;

(2) 試問小球在平衡點B附近是否存在相對于細管的徑向微振動?如果存在,求出該微振動的周期.

解析: (1) 設細管的角速度為ωA,小球在A點相對細管平衡時

(1)

小球在平衡B點滿足

(2)

小球由A處至B處過程滿足角動量守恒

(3)

聯立(1)-(3)式得

(4)

(5)

(2) 在轉動參考系中,小球相當于在有心力作用下運動,設小球距O點的距離為r,則其有效勢能為

(6)

其中小球的角動量

(7)

對(6)式求二階導數并把(7)式代入得

(8)

聯立(4)、(5)、(8)式得

(9)

故該微振動的周期

(10)

通過以上分析,對有心力作用下物體運動引入有效勢能,把二維平面運動問題轉化為一維問題來處理,不失為一種解決問題的好方法.