不同方法對南黃海重現波高計算值的影響

趙嘉靜，馮 曦，馮衛兵，李慧超

(河海大學 港口海岸與近海工程學院，南京 210098)

海岸工程的規劃和建設對一個國家的經濟發展起到帶頭作用。為了保證海岸基礎設施的設計與建設的安全穩定，如碼頭與港口的設計與施工[1-2]，需要對波浪參數有確切的掌握。波高極值資料對于工程的設計與施工都不可或缺。

波高的長期變化趨勢可以通過累積分布函數圖和重現期分布來表征，此方法廣泛應用于沿海極端波高的研究[3-5]。極值分析(EVA)在海洋、氣象、金融、交通等領域的應用十分廣泛，極值分析理論應用于極端波高的分析可追溯于Goda[6]、Mathiesen等人[7]和Menendez等人[8]，由于工程的需要，在中國近海海域已有基本的研究[9-12]。廣義極值分布函數(GEV)經常被應用于極值的統計分布，最常用的方法是對于長期數據，采用每年取一個極大值的方法進行擬合，缺點是往往會忽略每年發生的其他極端情況。對此有2種解決辦法：分塊取極值法和超閾值(peak-over-threshold，POT)方法[13-14]。分塊取極值法最常用的是采用取月極值波高的方法，即每個月取一個極值，盡可能統計到發生在全年的極端波高情況；POT方法即選取一個特定的閾值，對超過該閾值的值進行統計并分析。極端波高的長期變化趨勢一直以來備受關注，Komar等人[15]使用NOAA浮標測量數據對美國西海岸等地也做了類似的研究。

南黃海地區位于中國江蘇、浙江省沿岸，由于輻射沙洲的存在，近岸地形復雜(圖1-a)，同時受到季風影響，多臺風浪和風暴潮，出現極端水位情況較多[16]。現有的測站多位于沿岸且數據有缺失，不能完全表示出整個南黃海地區的長期波浪分布情況，因此不僅需要合適的極值計算模型，還需進一步分析數據長度對于重現波高計算的影響[13]。本文研究目的在于利用3種方法計算南黃海地區的百年重現波高空間分布，并進行比選，得到不同情況下的最優方法。同時，計算3種方法受到不同時間跨度的影響，為工程建設提供指導。

1 模型及極值計算方法介紹

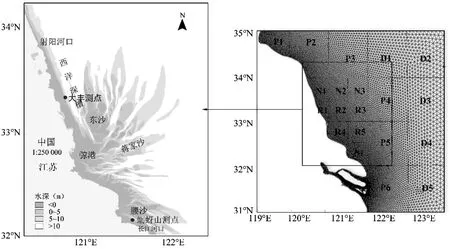
1-a 區域地形 1-b 網格區域

1.1 模型設置

本研究采用SWAN模型進行模擬，此波浪模型已廣泛應用于中國近海海域，模擬結果良好[17-19]。網格經度范圍119°E～124°E，緯度范圍31°N～35°N(圖1-b)，共有10 429個節點和20 097個單元，精度范圍從0.02°到0.11°(1 322～12 454 m)。利用歐洲天氣預報中心(ECMWF)1979～2018年共40 a的風場數據作為初始條件，時間分辨率為6 h，空間分辨率為12 km。物理過程考慮了包括白帽、破波、底摩擦、波-波相互作用在內的波能耗散機制。SWAN模型的控制方程如下[20]

(1)

S=Sin+Swc+Sbrk+Sbot+Snl4+Snl3

(2)

式中：N為波作用量密度，方程左邊第1項為動密度譜對時間的偏導，第2～5項分別為能量在x、y、σ、θ空間的傳播，Ci(i=x、y、σ、θ)為各個空間的能量傳播速度。方程右邊S為源項，包括能量產生項(風能輸入Sin)，耗散項(白帽耗散Swc，深度誘導引起的波浪破碎Sbrk，底摩阻耗散Sbot)及轉化過程(四波相互作用Snl4, 三波相互作用Snl3)，σ為相對頻率。

1.2 模型驗證

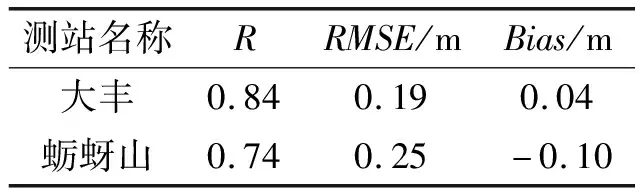
表1 有效波高的驗證參數

為了證明模擬結果的可信性，選取大豐(120.81°E，33.285°N)和蠣蚜山(121.568°E，32.147°N)2個浮標測點2013年的實測波高(Hs)數據進行對比。相關系數R，均方根誤差RMSE及偏差Bias如表1所示，大豐測站吻合較好，蠣蚜山測站由于浮標放置在狹窄的潮道中，潮流的影響較明顯，故在單純考慮風場的情況下模擬準確性不高。圖2為大豐測站2013年部分模擬值與實測值，可以看出除了實測數據有缺失的部分，模擬波高和實測數據擬合較好。圖3中給出了大豐測站模擬值與實測值兩者的線性比例的概率密度分布圖，實測數據與模擬值貼近45°線，說明SWAN模型能夠較準確地模擬本地區波高的時間變化。

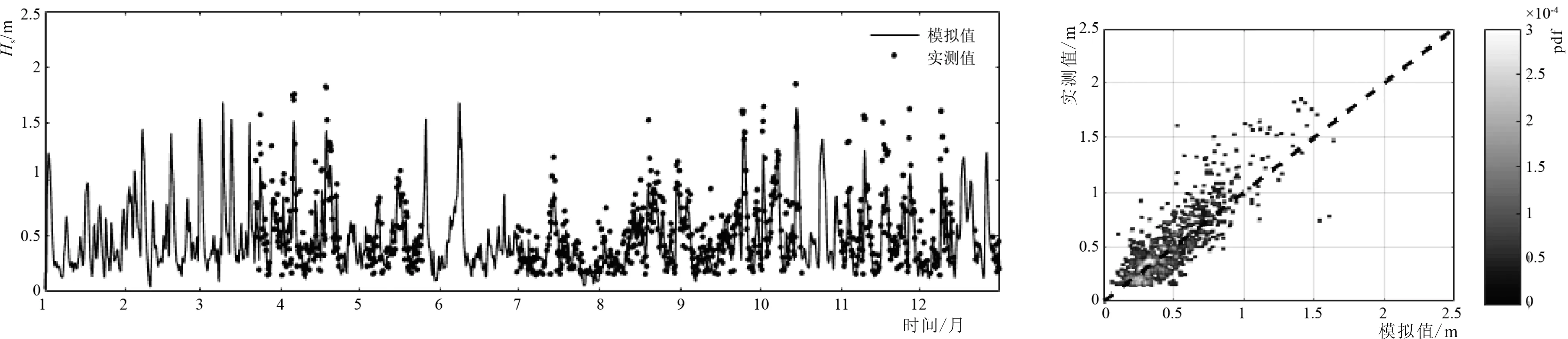
圖2 大豐測站模擬波高和實測數據對比

Fig.2 Comparison of simulatedHsand measuredHsat Dafeng station

圖3 大豐測站模擬波高和實測數據線性比例的概率密度分布圖

Fig.3 Linearly scaled probability density function(pdf)of observedHsversus modeledHsat Dafeng station

1.3 極值分布函數

1.3.1 GEV模型

在極值理論中，已經證明，對于足夠長的獨立和相同分布的隨機變量序列，大小為n的樣本的最大值可以擬合到廣義極值(GEV)分布中[21]，該分布具有以下累積分布函數

(3)

μ、σ和ξ是位置、尺度和形狀參數，與重現期T相對應的重現波高的求解可以使用以下方程

(4)

GEV經常被應用于極值的統計分布，最常用的方法是對于長期數據，采用每年取一個極大值的方法進行擬合，缺點是往往會忽略每年發生的其他極端情況。

1.3.2 基于POT方法的廣義帕累托分布模型(GP模型)

對于超過一定閾值的數據，滿足如下廣義帕累托分布函數

(5)

與重現期T相對應的重現波高的求解如下

(6)

POT方法比每月取一個極值的方法更能反映出極端天氣的發生情況，但是需要慎重給定取樣時間間隔和閾值。時間間隔的選取應結合不同地區的極端天氣發生情況，要保證盡可能多地考慮到極端天氣發生次數，且不至于在同一次極端天氣中選取多個極值。閾值的選取會直接決定取值的數量，過低的閾值會造成數據取樣數量大進而導致模型預測結果的偏低，過高的閾值會造成分布參數計算結果的劇烈變動[22]。

對于時間間隔的選取，已經有學者研究發現，極端天氣事件的發生間隔是隨著不同地區、不同年限而相互獨立的[22-23]，因此只能確定一個常用的合理值，常用3 d[13-14]。

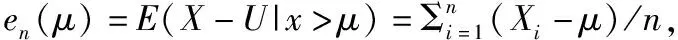
1.3.3 極值分布模型的適用性

本文以南黃海地區劃分的20個區域的40 a風浪推算數據為基礎，采用基于取年極值與月極值的GEV分布模型和基于POT的GP分布模型，分析兩種模型的適用性，并推算對應100 a重現期的重現波高。限于篇幅，本文僅選取了20個劃分區域中具有代表性5個區塊的進行詳細說明：輻射沙洲北部區塊N2、輻射沙洲中部區塊R2、輻射沙洲邊緣區塊P4共3個區塊(圖1-b)。

通常采用累積分布函數(CDF)圖和Q-Q圖來判斷數據與分布函數擬合的優劣。GEV分布的CDF圖如圖4所示，當各區域取年極值波高(圖4-a～圖4-c)和月極值波高(圖4-d～圖4-f)時，模擬值(虛線)與理論值(實線)均符合分布趨勢，說明GEV分布適用于整個南黃海區域的波高擬合。在Q-Q圖(圖5)上可以看出年極值和月極值取樣基本符合分布趨勢，基本分布在45°線(虛線)附近，說明兩者吻合良好。但在曲線尾部會有出入，預測曲線比實際偏低，即預測波高會小于實際值，這種現象在取月極值(圖5-d～圖5-f)時更明顯。

4-a N2區域取年極值 4-b R2區域取年極值 4-c P4區域取年極值

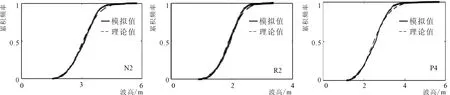
4-d N2區域取月極值 4-e R2區域取月極值 4-f P4區域取月極值

圖4 代表區塊GEV分布的CDF圖

Fig.4 The CDF plot of theGEVdistribution in the representative block

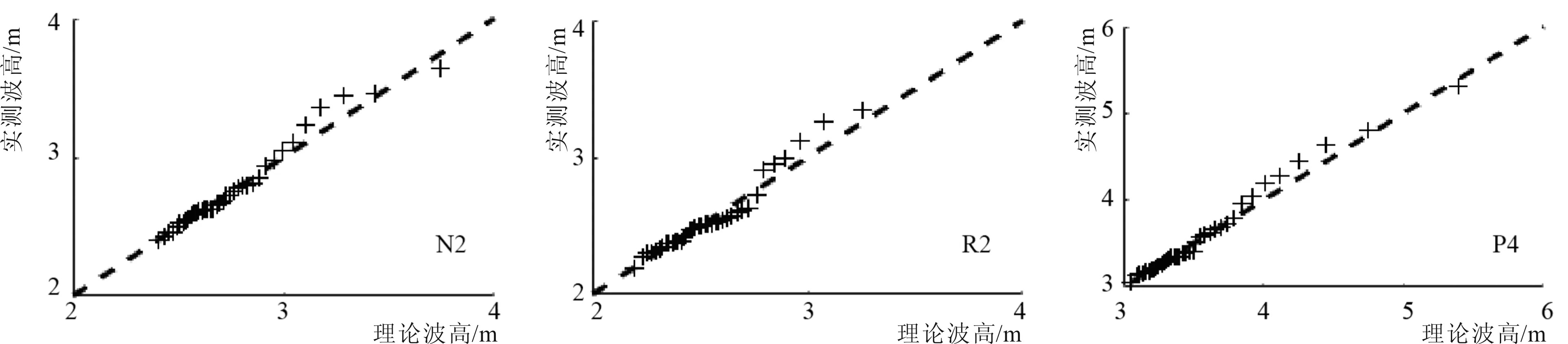
5-a N2區域取年極值 5-b R2區域取年極值 5-c P4區域取年極值

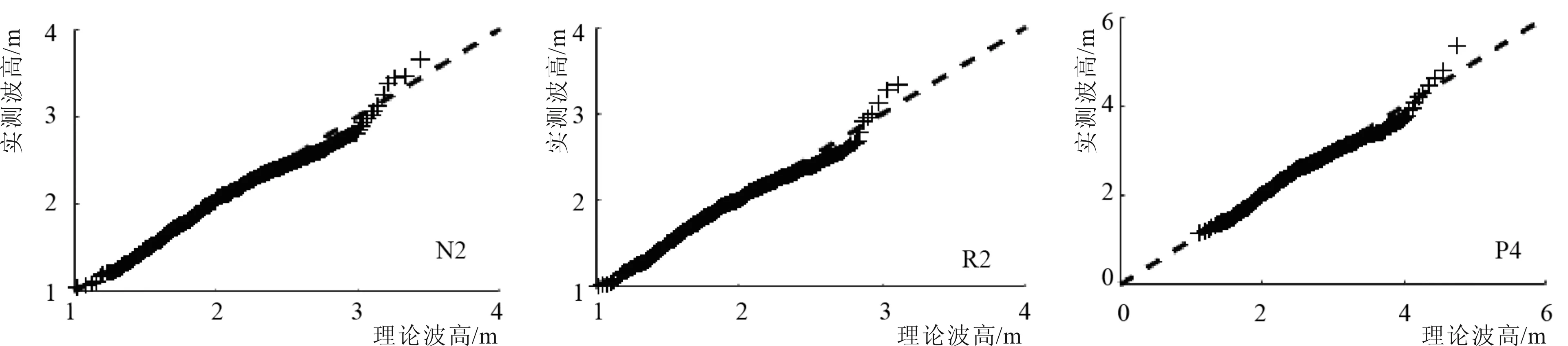
5-d N2區域取月極值 5-e R2區域取月極值 5-f P4區域取月極值

圖5 代表區塊GEV分布的Q-Q圖

Fig.5 The Quantile-Quantile(Q-Q)plot derived fromGEVdistribution in the representative block

基于POT方法的GP模型中時間間隔選為3 d，對于模型中閾值的選取，則根據超額均值函數確定。圖6所示為3個代表性區塊的超額均值函數圖。圖7所示為3個代表性區塊的平均剩余值圖，圖中實線代表形狀參數值Xi，上下兩條虛線為形狀參數估計值的95%置信區間的上下限。在超額均值函數和形狀參數滿足穩定線性狀態后來看，3個區域閾值結果分別為1.9 m、1.85 m和2.45 m。閾值確定之后，繪制滿足超過閾值GP分布的擬合圖，如圖8所示，真實值由點組成，而黑色線表示分布趨勢，縱軸表示GP分布函數。可見，選擇最佳閾值后，在3個代表區塊中，超出相應閾值的樣本均符合GP分布，除了中間部分稍微有所出入，頭尾兩部分預測狀況較好。

圖6 代表區塊超額均值函數圖(時間間隔為3 d)

Fig.6 The Mean Excess Function(MEF)in the representative block(Time span is △t=3 d)

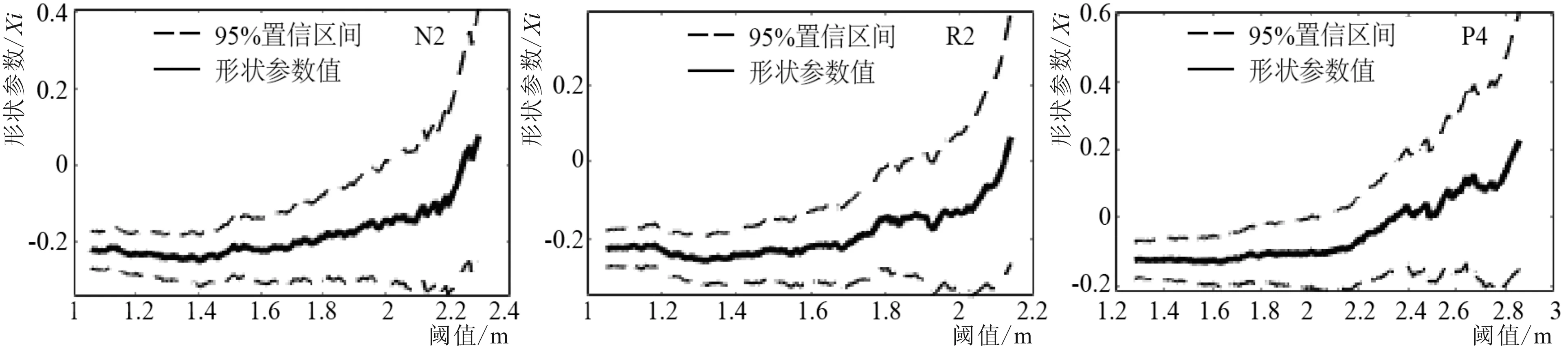
圖7 代表區塊95%置信區間的平均剩余值圖(時間間隔為3 d)

Fig.7 The mean residual life plot with 95% confidence intervals in the representative block(Time span is △t=3 d)

圖8 代表區塊滿足超過閾值的GP分布(時間間隔為3 d)

Fig.8 TheGPdistribution function plot meeting the peak over threshold in the representative block(Time span is △t=3 d)

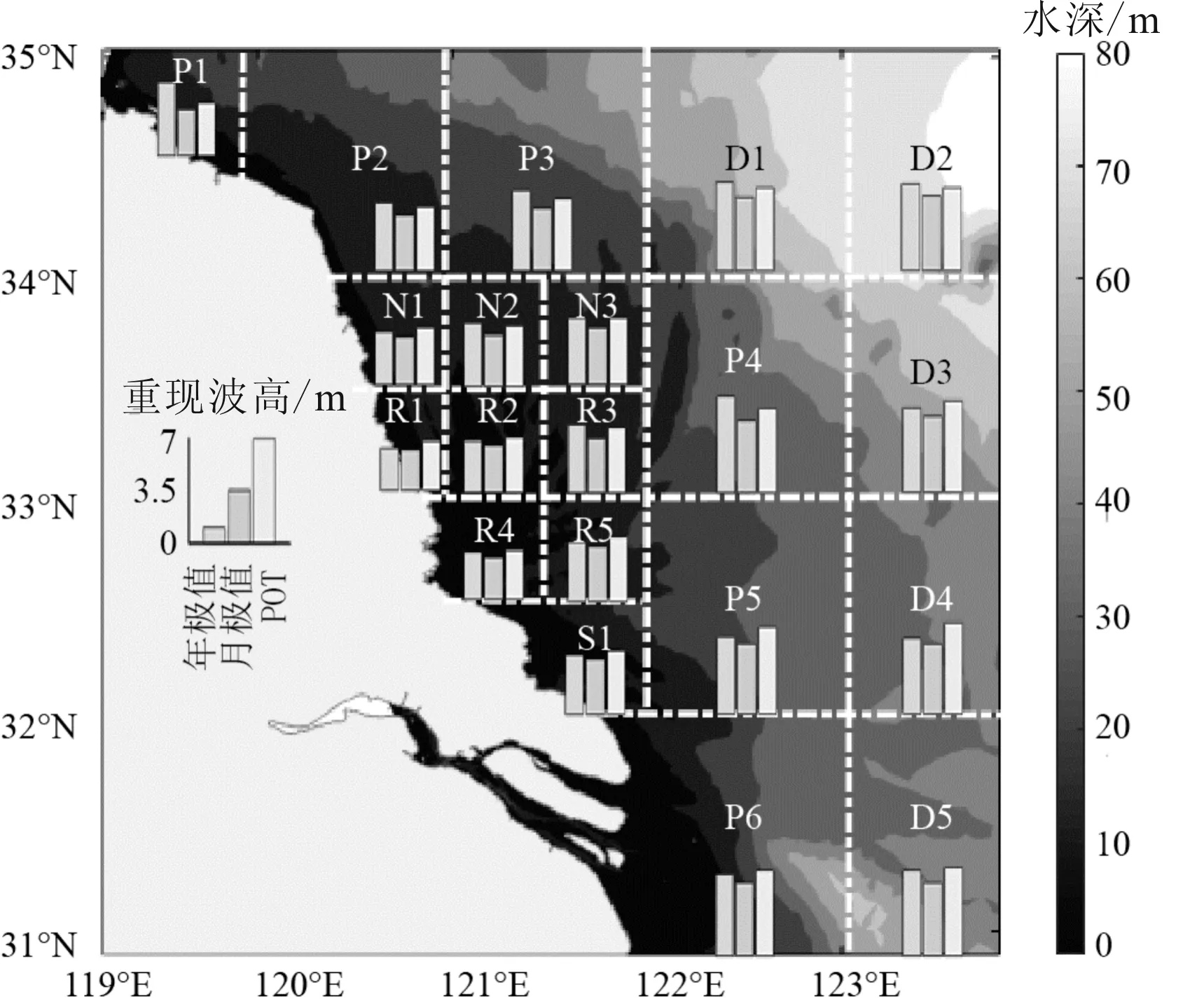
圖9 20個區塊取年極值、月極值方法與POT方法計算的百年重現波高對比

綜合之前采用取年、月極值的GEV分布和采用POT方法的GP分布來看，2種分布擬合均符合南黃海地區的波高分布趨勢。在所研究的分布均適用的情況下，分別用取年極值、月極值、POT方法獲得的數據，可以進一步計算得到對應分布函數下的重現波高。

2 結果

2.1 基于不同方法的百年重現波高空間分布

使用本文方法利用40 a的數據計算得到20個區塊的100 a重現波高統計如圖9所示。可見，采用GEV分布取年極值的方法比取月極值方法計算的百年重現波高明顯高，這是因為年極值僅考慮了每年最大波高的情況，忽略了其他極端情況。POT方法采用的GP分布擬合出的百年重現波高和采用取年極值的GEV方法相差不大，互有高低，顯然也比取月極值的GEV方法計算值高，這是由于POT方法平均每年取的極值數約為3個，并沒有像取月極值那樣每年取12個之多，忽略相對小的極端波高。

為了直觀地表述南黃海地區的100 a重現波高的分布特征，圖10給出了3種不同取極值方法所計算的百年重現波高分布圖。其共同特征是，重現波高以輻射沙洲為中心向呈輻射狀外圍遞增。不同點是，重現波高的較大值集中分布區域有所不同，取年極值方法的重現波高最大值出現于東北部深水區，POT方法位于東南部區域但范圍較廣，月極值方法大致分布區域則較為均勻。究其原因，可能是不同區域出現極端波況的頻率和極端波高值各有不同。東北部地區更偏向于每年發生最極端情況，其他深水區更多發生次極端情況且發生次數更為頻繁。

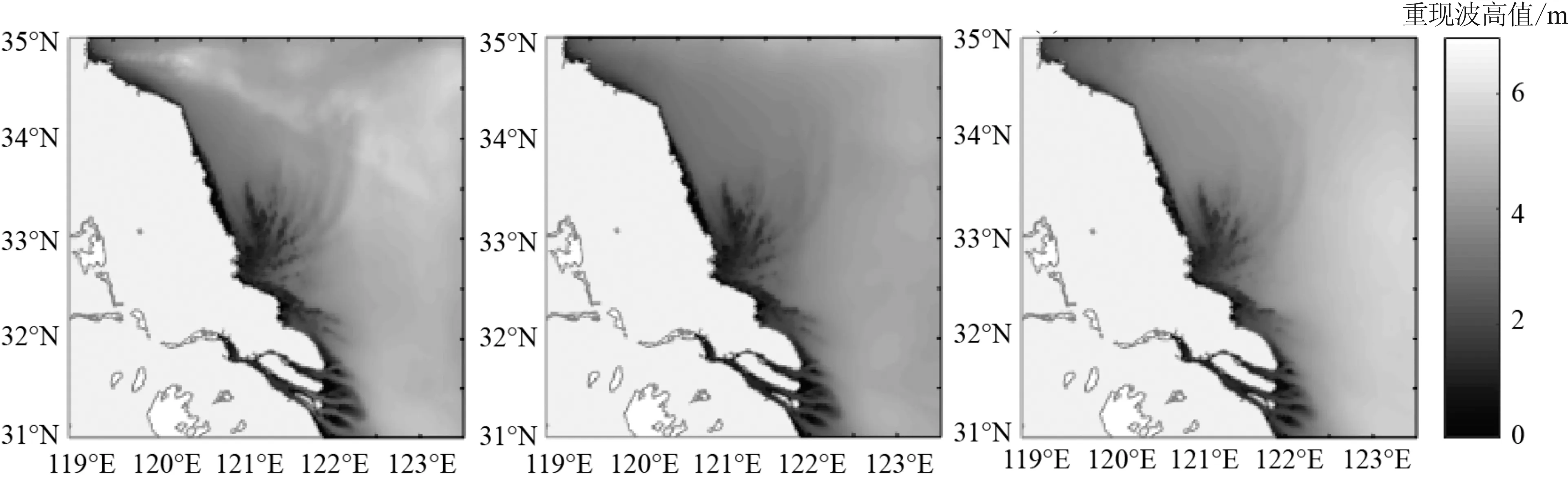
10-a 年極值 10-b 月極值 10-c POT

圖10 三種方法分別計算的百年重現波高分布

Fig.10 The 100-year return wave height distribution calculated by three methods

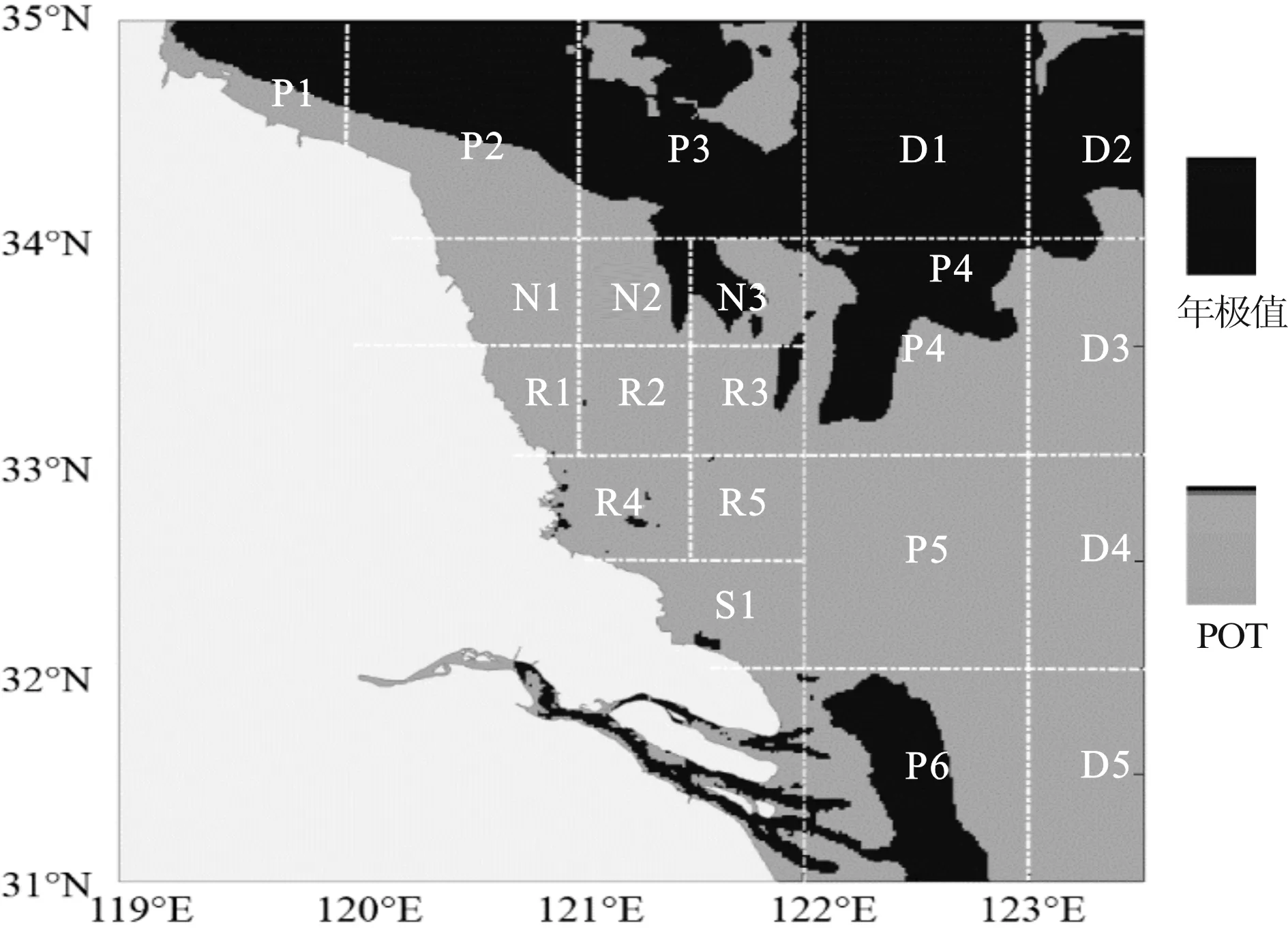
圖11 每個區域重現波高計算方法的最保守選擇

在圖11中給出了3種方法中，每個區域得到百年重現波高最大值時，即工程上最保守時采用的方法，可見在南北部地區取年極值方法計算的百年重現波高大，其他中部地區和輻射沙洲區域則基本以POT方法為大，說明這些地區在個別年份出現了多次高于正常年份的極端波況。

2.2 不同時間跨度對百年重現波高計算的影響

遵循工程上的取值思路，從最近的10 a數據開始，逐次增加數據長度，使用對應數據長度為10 a、20 a、30 a和40 a的2009～2018年、1999～2018年、1989～2018年和1979～2018年期間的數據。采用基于年、月極值的GEV分布和基于POT方法的GP分布計算了輻射沙洲內部的區域的百年重現波高，同時計算20～40 a相對10 a計算結果的增長率(表2～表4)。

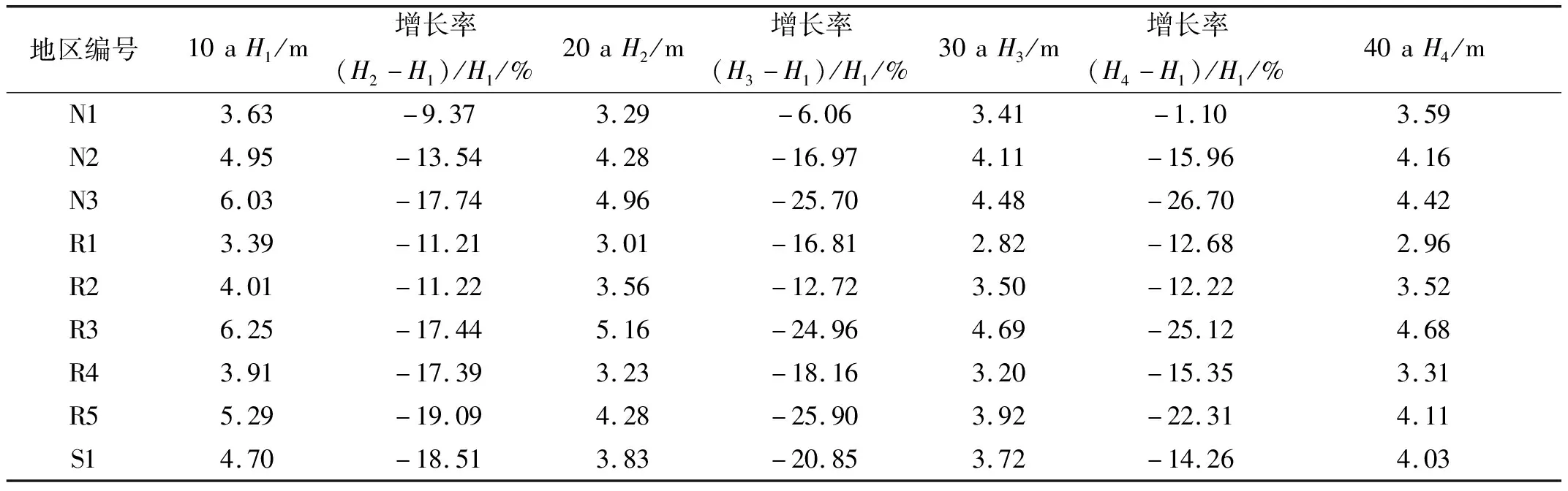
表2 基于年極值的不同時間跨度的百年重現波高及增長率

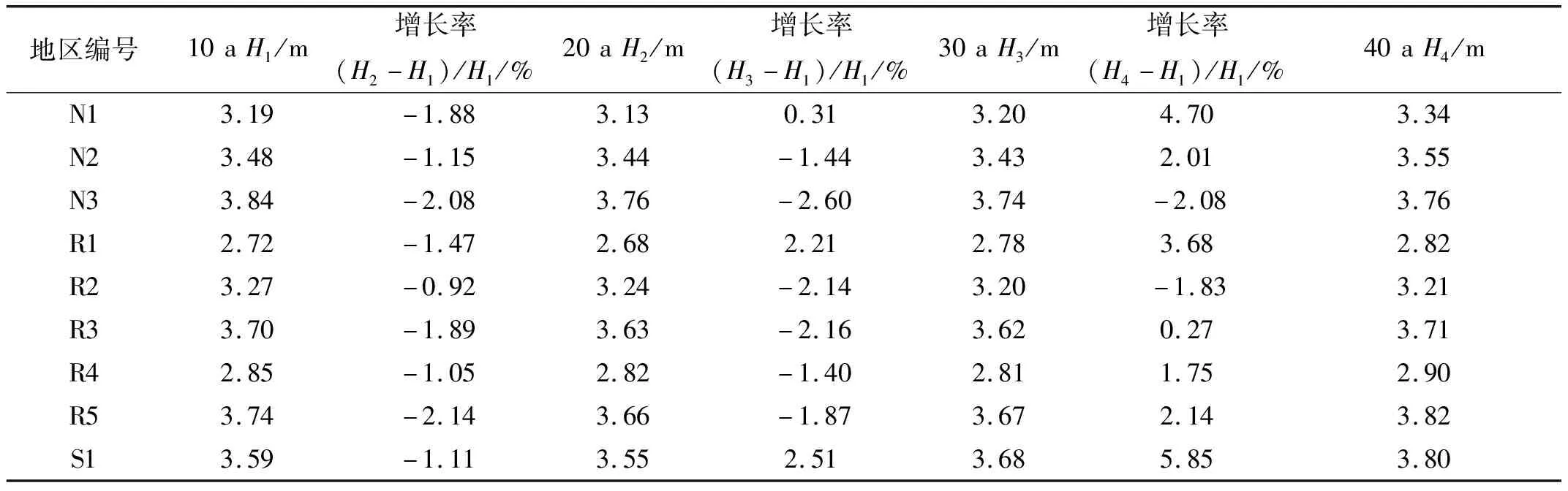
表3 基于月極值的不同時間跨度的百年重現波高及增長率

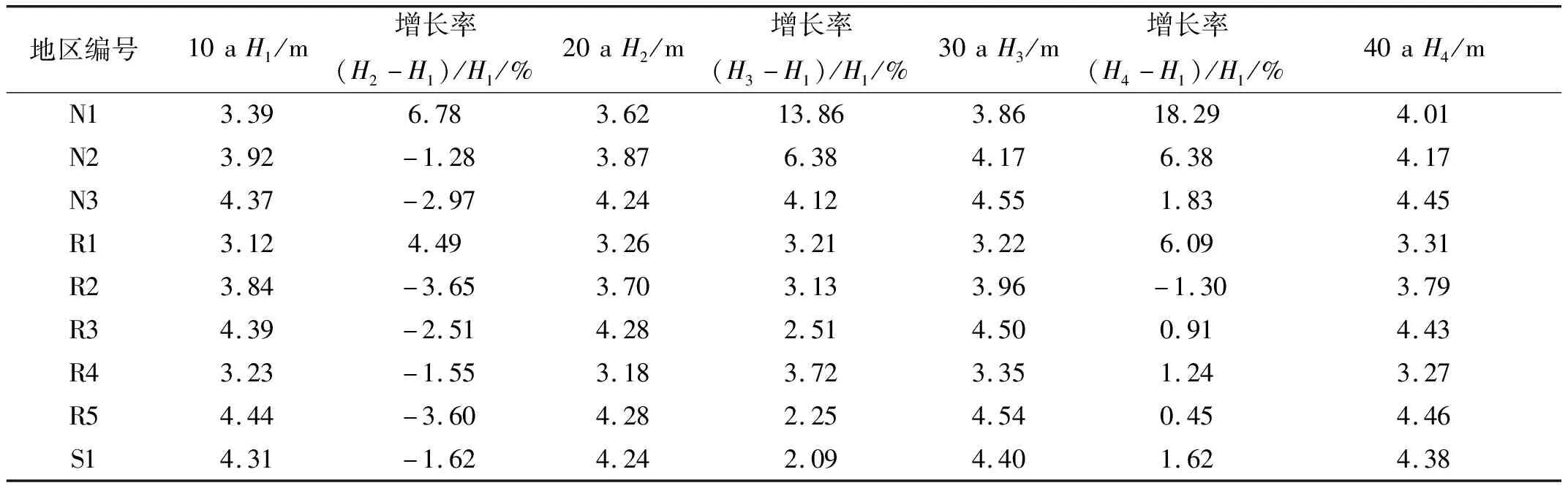
表4 基于POT方法的不同時間跨度的百年重現波高及增長率

從不同取值長度計算的百年重現波高增長率看，取月極值的GEV分布計算結果對時間跨度的改變不敏感，而取年極值和POT方法均受制于時間跨度的選取。基于年極值的方法取近10 a的數據計算的百年重現波高最大，且不同數據長度計算出來的值差別很大，這是因為每年取一個極值的情況偶然性大，所記錄的每一個極端波況對百年重現波高結果都會產生明顯的影響。取年極值的方法計算的重現波高值隨著取值年段長度增加而減小，即較長的數據集計算產生較小的重現波高，這與Mazas等[25]的發現相同，一方面可能是短期數據集的偶然性導致，另一方面可能是近10 a的極端天氣情況發生較之前更為頻繁。

取月極值的方法計算結果最為穩定，但是由于取樣數量較多，影響相對小的波高也被考慮到，導致計算結果偏于不安全。POT方法的計算結果的穩定程度介于前兩者之間。

取月極值方法計算的百年重現波高隨著取值年段長度變化雖然穩定，但是明顯偏小，取年極值計算結果最大，而POT方法計算的大小介于前二者之間。如果考慮到工程上偏于安全的情況，即在POT方法和取年極值方法中在不同地區選擇各自最安全的重現波高值。

3 結論

本文利用第三代近岸波浪模型SWAN在中國南黃海地區模擬了長達40 a的波高數據，模擬波高和實測數據擬合較好。

基于年極值和月極值的廣義極值分布(GEV)和超閾值取值方法(POT)的廣義帕累托分布模型(GP)在南黃海地區適用。利用40 a模擬波高計算得到的百年重現波高在輻射沙洲北部地區計算的結果差別最大，采用月極值所得極值偏小，輻射沙洲南北外圍地區采用年極值計算的重現波高大，其余地區則用POT方法計算出的結果較大。如果考慮到工程上偏于安全的情況，即在POT方法和取年極值方法中在不同地區選擇各自最安全的重現波高值。

不同時間跨度的計算結果表明，取月極值的GEV分布計算結果對時間跨度的改變不敏感，而取年極值受之影響最大，POT方法介于兩者之間。取月極值方法計算的百年重現波高隨著取值時間跨度變化雖然穩定，但是在不同時間跨度下百年重現波高值明顯偏小，取年極值的百年重現波高值最大，而POT方法計算的大小介于前二者之間。