網約車平臺VCG雙邊競價交易機制設計*

周樂欣，陳文端 ，何康

（1.貴州大學 經濟學院，貴州 貴陽 550025；2.貴州大學 管理學院，貴州 貴陽 550025）

0 引言

網約車平臺是一個完美的市場組織者，它的顛覆性出現改變了出租車市場［1］，改變了城市居民的出行方式［2］。該平臺能夠獲取在某一地段內有出行需求的乘客和空閑的司機，乘客能夠更有目的性的尋找出租車進行打車，大大減少了人們的出行成本，也為空閑的車輛提供出行服務，補充了出租車市場車輛不足的情況，在一定程度上緩解了“打車難”的問題［3］，在乘客司機雙方信息交互的基礎上充分利用了社會的資源。大數據條件下，競價交易模式能夠突破信息不對稱及交易局部化問題［4］。VCG機制是針對網絡空間無法對數字產品或服務進行價格估值的情況下，以Vickrey提出的單品次價拍賣為基礎，由Clarke和Groves推廣到更一般的多品次價拍賣機制，并啟發了一系列以說真話為最優策略的機制設計［5-6］。VCG拍賣定價機制是定價機制的里程碑，已經被證明是最有效的拍賣定價機制，它的出現提供了一種可信機制的拍賣框架，并且應用于諸多領域。VCG機制假想競拍者首先提交對于每件拍品的報價，由拍賣系統以社會最優的方式給每個競拍者分配拍品，競拍者得到某件拍品支付的費用由其獲得這件拍品對其他競拍者造成的損失來表示。這個機制有兩個特點：一是該機制能激勵競拍者按照其對拍品的真實估值出價;二是該機制可以達到社會最優分配。這個機制是有效的，激勵相容的，以及個人理性的，可以保證用戶之間分配資源的公平性［7-8］。網約車服務市場測試數據顯示，司機和乘客共享信息能夠減少60%～90%出行費用，且弱化司機之間的不良競爭［9］。周樂欣（2019）等基于雙邊報價機制對網約車平臺的交易匹配進行了研究，交易價格為統一價格，沒有對各交易主體的市場進行更進一步反映［10］。

本論述使用VCG機制來構建一個能夠在網約車平臺使用，達到合理分配乘客與司機的機制，而達到上述效果乘客只需要支付相應合理的價格。網約車平臺作為組織者，在現有的技術條件下先獲取乘客和司機雙方位置信息，將一定區域內的乘客與司機進行組織。然后獲取乘客與司機雙方對于此次打車服務的報價信息，并依據這些信息由此機制給出合理分配結果以及乘客與司機的支出、收入。而本論述設計的這個機制滿足了參與理性約束、預算平衡約束，并鼓勵交易雙方能說真話，使交易雙方分配交易機制中產生的所有交易剩余，最后本論述通過建模仿真模擬分析交易雙方的行為以及實現了這個機制。

1 網約車競價機制設計

1.1 機制描述

VCG競價打車機制是一個雙邊競價機制，通過設定的匹配規則和支付規則來確保交易雙方能夠在交易過程中提供其真實報價，利用機制來讓交易雙方“說真話”，即司機報出真實成本，乘客報出真實支付意愿。基于此機制可以快速搜索匹配相應的乘客和司機進行交易，并設置相應的支付規則來進行“市場出清”，乘客支付費用。這一切的實現是以社會福利最大化的角度來進行打車資源最優化的配置。交易過程如圖1所示，即（1）現有的打車方式和網約車平臺的基礎構建不變；（2）乘客和司機將各自的位置信息傳送到網約車平臺的服務器，同時乘客將自己要前往的目的地、此次打車的費用報價，司機將自己愿意運送乘客的車費報價一塊發送到了網約車平臺，平臺機制將這些信息進行處理，最終確定哪位乘客和哪位司機進行匹配，并確定乘客和司機各自的支付和收入；（3）乘客與司機完成交易。

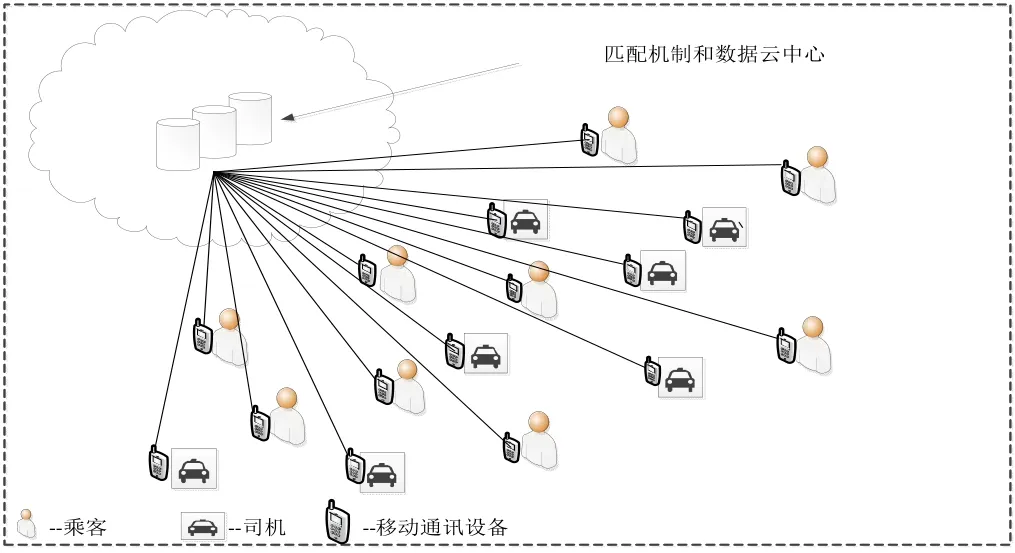
圖1 基于數據云的網約用車雙邊競爭性報價交易平臺

本論述運用的是VCG競價機制來構建網約車平臺匹配機制。首先運用的是競價的模型，關于競價交易遵循如下兩個原則：（1）價格優先。當有多個競爭者進行報價時，對于買方而言，買方出價高者擁有優先交易權，對于賣方而言，賣方報價低者可以優先選擇交易;（2）時間優先。當買賣雙方的物品及價格相同時，先進入市場報價者優先交易。

1.2 機制設計

本論述基于乘客與司機的報價，設計系同的匹配規則和支付規制，以保證市場的出清和市場價格生成，從而使乘客和司機達成交易。

1.2.1 匹配規則

假定在某一范圍不大的地區內，各有一定數量的司機和有打車需求的乘客。在某一時間段內這些乘客同時提出打車的需求，而司機則能夠為這些乘客提供出租車服務。本論述設定乘客的集合為P，其中Pi∈P ，i=1，2，…，n，Pi代表任意乘客；司機的集合為D，其中 Dj∈D，j=1，2，…，m，Dj為任意一個司機；乘客與司機的報價會根據網約車平臺以往的交易記錄來給定一個基礎的價格，這個價格為每公里的單價，作為參考價格，交易雙方根據這個基礎價格進行報價；對于乘客 Pi其愿意為其行程提供的報價為（bˉi，bi），bˉi表示乘客行駛里程小于θ時支付的起步價報價，bi表示乘客行駛里程大于θ時超過部分支付的單價報價；其出行的距離為Li；而司機Dj愿意搭乘乘客而提供的報價為（sˉj，sj），sˉj表示乘客行駛里程小于 θ時司機的起步價報價，sj表示乘客行駛里程大于θ時超過部分司機的單價報價；定義xij為乘客和司機的匹配關系，xij=1表示乘客Pi和司機Dj達成交易，xij=0則相反。優化目標為社會福利最大化。?為乘客和司機的所有可能存在的分配集合，乘客和司機的最優匹配方式為X（P，D），X(P，D)∈?。當乘客司機的匹配方式為X(P，D)時系統的社會福利最大，社會福利U的計算定義為：

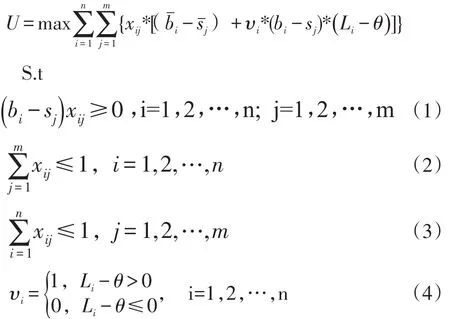
約束（1）表示參與交易的乘客的報價是應該是大于司機的報價；約束（2）表示每個乘客能夠匹配到的司機的個數最多為1；約束（3）表示每個司機能夠匹配到的乘客的個數最多為1；約束（4）表示當乘客的出行距離大于 θ時，υi=1，否則 υi=0。

1.2.2 支付規則

本論述在定義一個概念效用W，效用的意義是當前這個競價系統中某一個人的報價對于系統中的社會福利U的影響。即如果系統中剔除這個交易者后，對于系統最大社會福利值U的減少值。則對于乘客來說每個參與交易的乘客的效用WPi以及每個司機的效用，其中，U為市場中乘客與司機交易的最大福利值，Un{Pi}為系統中將乘客Pi剔除出系統后的社會最大福利值。Um{Dj}為系統中將司機Dj剔除系統后的社會最大福利值。

根據U的計算公式可以知道，U的取值是對應所有的乘客司機匹配方式?中選取最優的匹配方式X（P，D），這樣的匹配方式經過計算能夠使U值最大。顯然一般情況下U值對應的匹配方式是唯一的。所以參與交易的人群中剔除一個人之后，這個最優的匹配方式X（P，D）必然會發生一些變動，比如在其他交易者不變的情況下又新加入一個交易者，又或者X（P，D）完全改變又有新人參與交易中來。而顯然新的交易者的報價顯然是不如被剔除人的報價有競爭力，不能提供高于被剔除人的社會福利。顯然對于乘客U≥Un{Pi}，對于司機U≥Um{Dj}。每個乘客和司機的效用可以看作是這兩者對于系統的貢獻值。當乘客的高報價以及司機的低報價情況下可以根據U的計算公式可知，U的值將會越大。但乘客如果他的報價小于所有的司機的報價，那么他將不會參與到機制的分配。同理對于司機如果他的報價大于所有的乘客的報價，他也將不會參與到機制的分配。所以為了鼓勵乘客以及司機能夠更多的參與到交易當中去，本論述將每個乘客司機的效用作為獎勵發放給每個交易參與者。

（1）乘客支付：乘客Pi對于他的獎勵是減免其在報價中承諾支付的費用，獎勵的費用為其效用，其具體支付如下：EPi=bˉi+bi*υi*（Li-θ）-WPi；

（2）司機支付：司機Dj的獎勵是在其報價的基礎上加上他的效用，在完成交易后能夠得到的收入為：

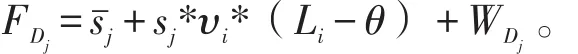
根據上述每個乘客和司機的每個人的支出和收入可以計算出在這個市場中所有的乘客的支出和收入之和。所有乘客的所有支出之和從中可以看出SumP與SumD的值是不一定相等的，無法保證預算平衡，也就意味著這個機制如果沒有外部的補貼下，在實際運行過程中乘客支付的費用和司機的實際收入不一樣，這顯然沒有實際意義。所以本論述對傳統VCG機制進行變形，對設定的乘客和司機的支付進行一定的修改，根據每一個乘客和每一個司機的效用為基準進行計算。所有乘客的效用之和為

為實現預算平衡，現修正每一位在系統中的交易者的效用，其效用為該交易者的效用占系統中所有交易者的效用的比例乘以市場中的最大社會福利，即：最終乘客和司機的實際支付和收入分別為：

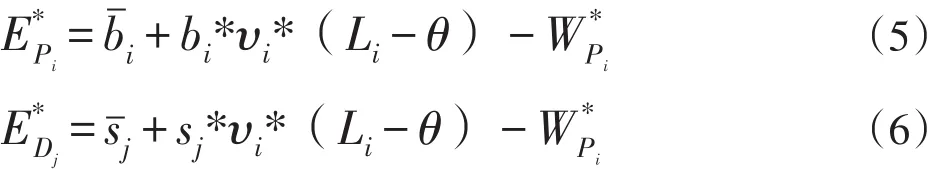
現證明市場中全部乘客的支出和全部司機的收入已經達到預算平衡。由于所有乘客支付：減可得：

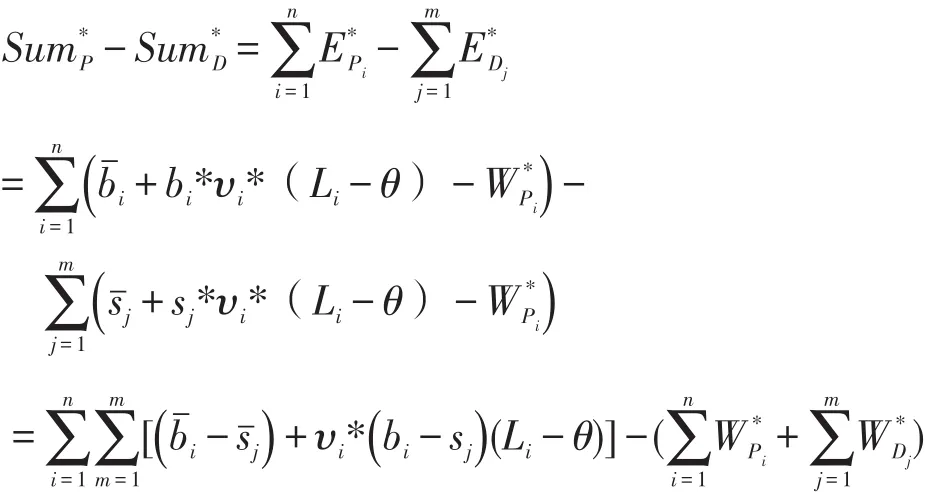
根據設定，系統中的社會最大福利值U為

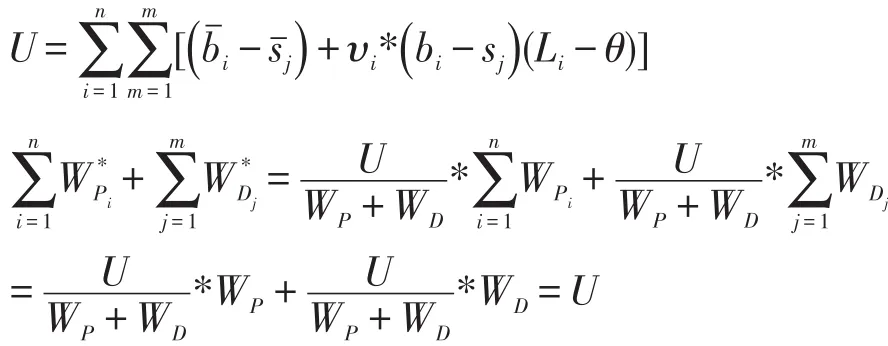
2 交易者報價行為分析

對于在市場中的交易者來說，交易雙方的交易信息是互相不知情，所以不可避免地市場中交易者可能為達成交易而進行不誠實報價，但本論述設計的機制可以保證這樣的情況不會發生，此機制滿足參與理性約束（參與交易比不參與交易的收益大）和激勵相容［5］原則（即交易者在交易過程中“說真話”）。對于交易者來說如果其能夠根據我們設計的機制競價成功，則其個人效用W非負，如果沒有競價成功，則其個人效用W為0。顯然參與交易競價成功的時候的收益是大于沒有參與時的收益，滿足參與理性約束。

現以乘客為例，可以分為兩類，一類是以能夠達成交易為交易目標的交易者，一類是以能夠最大收益即最少支付為交易目標的交易者。

（1）對于以達成交易為目標的乘客，市場中有兩種人，即能夠支付較高打車費用的乘客和有真正需求的打車人（比如因病送醫等有緊急事情的人），將這兩種人都看作是有強烈打車意愿的人。但此次打車對于各自的價值卻并不一樣。對于前者相對于普通人其意愿付出的價格可能會高一點，但對于有緊急事情強烈打車愿望的人來說這次打車的價值顯然是高于前者對于此次打車的費用認知。如果是因病送醫急需用車，這類人顯然會提出顯著高于日常價的報價。競價雙方對市場中的情形是不了解的，所以當乘客和司機進行報價的時候，對于競價雙方，乘客的報價如果過低，市場中高于此乘客報價的司機將不會有機會和此乘客配對。那么以達成交易為目標的乘客如果希望獲得更多的與司機配對的機會必然會以高于市場中的參考價格，盡可能達成交易，而這個報價對于他個人來說就是其自身的誠實報價。但不可避免地會出現不誠實的報價，對于低報價的乘客，如以達成交易為目標這不是他的最優策略，因為他可能無法打到車。而高報價確實能打上車，當乘客高報價獲得了打車的服務，就會使得其效用為負。顯然對于乘客依據其個人能力以及此次出行的服務對其自身的價值來進行報價顯然是最符合其利益的行為。

（2）而對于以盡可能減少支付為目標的乘客，顯然這類人在市場中可以按照傳統的打車中的匹配機制進行處理。這類人在市場中不會出現高報價的行為，因為高報價與其行為相悖。當市場中乘客多、司機少的時候，這類乘客的報價與其他乘客相比是沒有競爭力的，顯然在這一輪報價之后他有很大的概率是無法上車的。那么他就只能在下一輪的報價中進行報價，由此而損失時間。

綜上，對于乘客，如果其報價為x，真實報價為c。如果x＜c為其低報價，則其可能失去交易的機會，不滿足參與理性約束。如果高報價，即x＞c，可知其個人效用會增大，并能夠參與到交易當中去，但其收益即獲得打車結果與報價為c的時候相比并沒有改變，而高報價還會可能相應的增加其需要支出的費用。所以對于乘客來說真實報價即x=c時才是其最優報價策略。對司機而言，情況類似。

3 交易者行為仿真分析和算例

3.1 數據生成及計算

通過使用編程的方式來對VCG雙邊競價機制進行驗證，使用java編程語言對描述的VCG打車機制進行模擬，使用的軟件是Eclipse。在這個模型中，先是在市場中設定10個乘客與10個司機。乘客設定的屬性為單位報價與他的需求量。每個乘客的報價為（10，0.5）的正太分布，出行距離為（10，30）的平均分布。每個司機設定的屬性為報價和他能夠提供的數量。每個司機的報價為（20，0.5）的正態分布，可提供的旅程距離為（30，50）的平均分布。具體解答流程如下：（1）先構建一個n*m的數據矩陣（n為乘客的個數，m為司機的個數）；（2）為求解出合適的乘客司機一一匹配方式，將乘客和司機的數據轉化為指派模型對應的數據，再進行求解。在這個n*m數據矩陣上的每個位置上填上對應的數據，數據為乘客的報價-司機的報價；矩陣對應數據 Aij，表示第i行，第j列的數據，也即第i個乘客的報價與第j個司機之間的報價之差。然后乘以對應乘客的出行的距離，生成一個數據矩陣。（3）通過使用指派模型的算法［11］。對上述數據矩陣進行求解，可以得出一個乘客與司機的一一對應的匹配方式，再根據設計的支出和收入規則，計算結果。通過將使上述矩陣指派模型中的所有值累加可得系統中的社會總福利值U=2109.29，通過這個U可以計算出乘客的效用，從而計算出每個乘客與司機的效用和支出和收入。

3.2 仿真分析

這里的報價可以理解為買賣雙方的真實報價。對于乘客這是乘客為滿足自身需求數量的前提下，其自身資金能夠提供的最高單位報價。例如對于id為1的乘客，他的報價為19.32，需求的數量為22.0。則他能夠提供的資金最高為19.32*22.0=425.04。對于這個乘客如果當他成交時系統會給他一個價格，這個價格根據VCG機制獲得。如果這個價格與他的需求數量相乘大于其能提供的最高資金425.04，則這個乘客將無法支付。根據本論述的機制當他能夠支付更高的價格的時候他一定會報更高的價格。本論述設計的交易機制是匹配所有的乘客與司機的報價。只有在乘客的報價超過一部分司機的報價后，此機制才會考慮這個乘客的報價，進而參與到計算最大效用的計算中去。為驗證模型能否真的符合競價交易的原則，通過對買賣雙方的初始數據進行浮動，以模擬在實際情況中如果出現有人不誠實報價或者串通報價的情況下對這個交易機制的影響，分別在開放系統中作如下模擬。

3.2.1 封閉系統的模擬

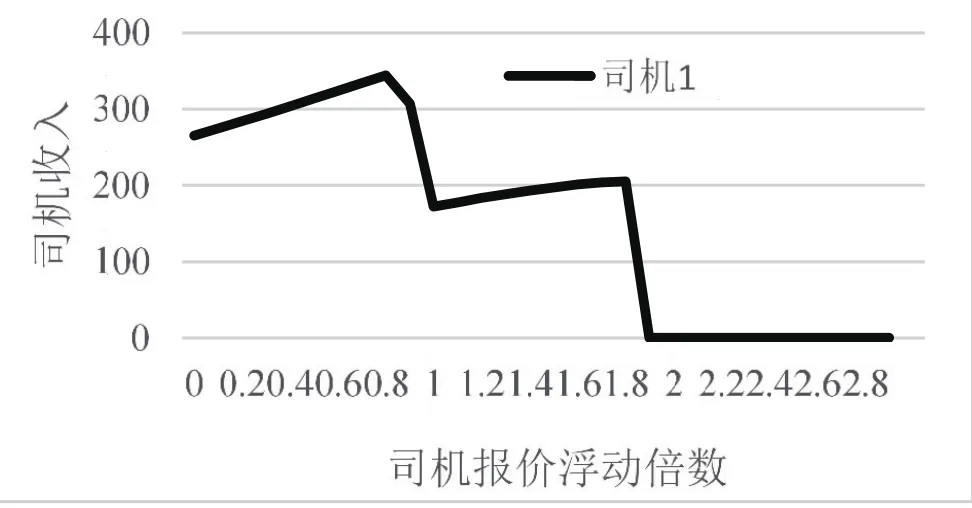
圖2 司機不誠實報價對個人收入的影響

與此同時在封閉系統內，即10個乘客和10個司機的交易情況下，以司機為例，司機的報價在初始報價上浮動，浮動倍數屬于區間［0，3）。結果如圖2及圖3所示。由圖可見，一般情況下若司機為了能夠達成交易，其將會進行低價報價，可以看到在低于司機誠實報價的價格之下，司機的收入是隨著報價升高而增加的。對于司機而言越低的報價雖然能使其參與交易，且個人效用越高，但對其收入并沒有提高。而如果為了所謂的增加收入而提高報價可以看到其收入相對于誠實報價階段并不會增加，反而是降低的。隨著報價的升高，其還會面臨失去交易的機會。從圖2可以看出對于司機來說在封閉系統中對其最好的策略就是其能夠誠實報價，當其報價在誠實報價周邊浮動時，對于其個人的利益能夠達到最大，收入最大，而不是單純的提高報價。

以上是設定的10個乘客和10個司機的交易情況，屬于封閉的交易系統，沒有外界的影響，模擬了20個人的交易情況。但實際情況中很顯然乘客與司機的數量是不一定相同的，乘客遠多于司機是較常見的現象。接下來要研究的是當系統中某個交易者不誠實報價下，如果有新的交易者參與到了這個交易，對這個交易者的影響。

3.2.2 開放系統的模擬

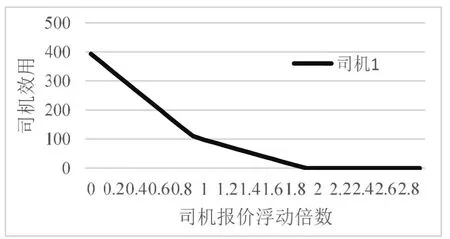
圖3 司機不誠實報價對個人效用的影響

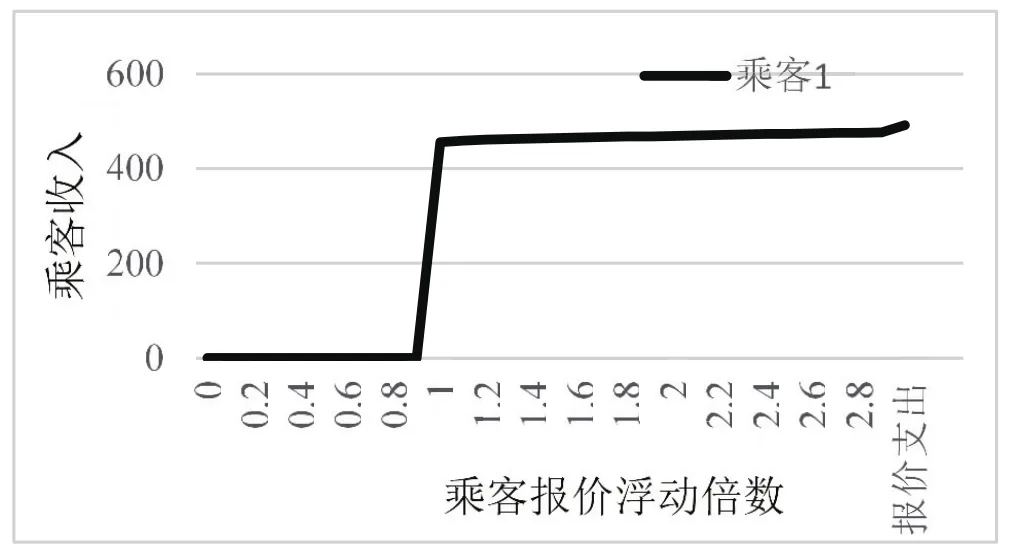
圖4 乘客不誠實報價對個人支出的影響

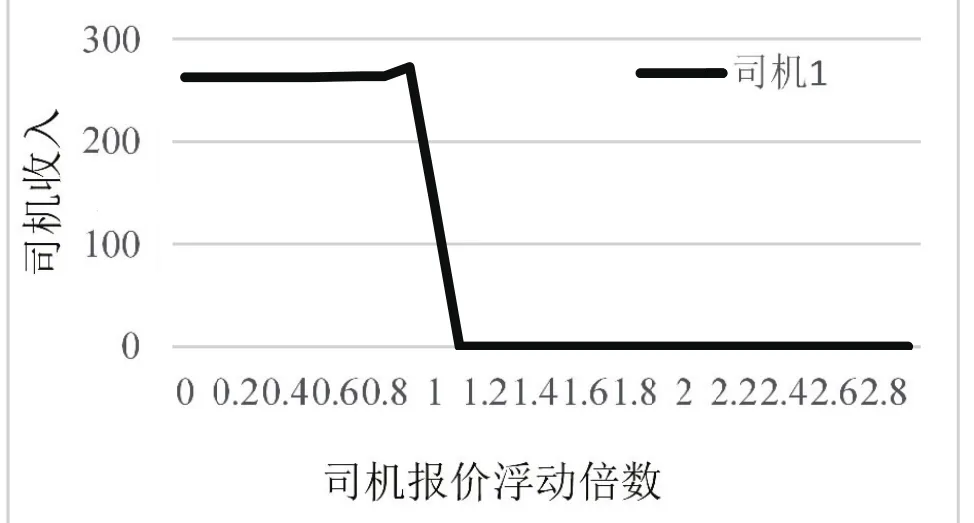
圖5 司機不誠實報價對個人收入的影響

（1）模擬乘客的不誠實報價。和在封閉系統中模擬一樣，對每一個乘客的報價進行價格浮動，但是市場中會添加入新的交易者，由此得出每個乘客在不誠實報價情況下對于支出價格的影響，如圖4所示，橫軸為乘客報價不同的浮動倍數，橫軸最后一項為乘客誠實報價情況下對應的支出，縱軸為乘客的支出和效用。可以看到當乘客報價低于一定價格之后可以知道其將不會參與交易，個人支出為0。然后當超過一定價格之后可以看到乘客的支出在一定范圍內變化不大。可以得知在乘客的報價有競爭力的情況下對于乘客來說，其報價的多少對于最終的交易支出并沒有太大影響。這對乘客的要求就是如果其為了交易報價必須能夠達到一定程度。如果為了能夠達成交易其不誠實高報價，也許其能夠達成交易，但是其實際需要支付的價格將會大于其能夠支付的價格，此行為將為交易人帶來負效用，所以不為占優策略。

（2）模擬司機的不誠實報價。對于司機的報價浮動，模擬不誠實報價，如圖5所示。對于司機來說可以看到當在一定范圍內，司機的報價浮動對于其最終的收入幾乎沒有影響，這里可以理解為在這個報價范圍內，只要司機的價格有競爭力，他就會參與到交易中去，那么他最終的收入就不會改變。司機的低報價可以認為是為了能夠更好的參與交易。但如果希望能夠獲得更多的利益，司機在誠實報價的范圍旁邊的價格對應最終收入是最大的。所以對于司機來說，其最優的報價策略就是其誠實報價，又或者在誠實報價周邊浮動報價，這樣才能給其帶來最大的收入。

4 結論

當前網約車市場中對于在車少人多的情況下，如何合理的分配網約車，沒有很好的機制去解決這一問題。現今網約車市場中對于這類情況主要是通過乘客排隊等候方式來依次等待服務，此外乘客通過加價的方式來獲取優先坐車的權利。一般情況下會在有特別緊急的事情下才會使用網約車的加價功能，來提前上車，但如何真實評估價值是關鍵。本論述構建基于VCG機制的網約車平臺交易機制，并通過理論證明了設計的機制滿足參與理性約束、交易者說真話原則、預算平衡約束。通過模擬仿真乘客與司機在系統中不誠實報價，交易者在設計的系統中只有說真話才是能夠使其達到最大利益的決策，驗證了交易者在這個系統中是說真話的。最后通過編程模擬實際路網情況，在平面立體上模擬乘客與司機在使用這個機制進行報價，通過設計的計算邏輯，算出了乘客與司機在這個系統中的匹配方式以及最終的乘客支付和司機收入，實現了我們設計的交易方式。