論學生添加輔助線能力重要性及培養策略
徐華

對于初中數學來說,幾何內容的學習是十分重要的部分,一方面能夠增加學生學習幾何知識的興趣與趣味性,另一方面還能夠全面的掌握具有實用性的知識,從而更好地進行幾何問題的解決。與此同時也能夠更好地對學生的空間思維建構能力以及邏輯思維進行培養。在進行有關幾何方面題目證明的過程中,為了能夠更好的進行問題的解決和證明,通常采用輔助線添加的方法。通過輔助線的添加能夠將較為復雜的問題進行簡化,然而在實際應用中,輔助線的添加會存在這樣或那樣的問題,對于學生來說,實際應用過程中仍然無法很好的掌握,這就要求任課教師在教學過程中側重學生這方面能力的培養。
1 輔助線的重要性
在進行數學的學習過程中,輔助線的添加是十分重要的方式,與此同時它也非常重要。對于初中數學來說,其作用主要體現在以下幾個方面:首先,通過輔助線的添加能夠有效地將復雜的幾何問題簡單化,從而降低問題的解答難度,同時輔助線的添加并不會對原有的幾何圖形造成影響。輔助線添加前后,幾何圖形中的邊、形狀、角度、大小都保持不變,這樣能夠提升學生解答問題的速度和效率;其次,利用輔助線能夠為原有的幾何圖形添加一些隱性的條件,這些隱性條件伴隨著輔助線的添加能夠得以顯現,利用這些隱性條件能夠為我們的推導與演算過程提供幫助,從而尋找到相應的規律,完成解答;最后,原有的幾何圖形會給我們提供一些顯性的集合條件,但是有些時候這些顯性條件是缺乏關聯的,因此需要通過輔助線的添加來完成這些條件的組合,從而更好地為題目的解答來進行服務。
對于如何解決初中數學的幾何問題,當面對復雜的幾何問題束手無策時,無論是學生還是老師都會選擇對復雜圖形進行輔助線的添加從而實現圖形的切割,形成數個簡單圖形,并形成一些可以借助的有利條件。從本質上看,輔助線的添加是為了實現問題的簡化,這主要是考慮到題目中所提供的淺顯條件無法對問題進行很好的解決,而通過輔助線的添加能夠為解題提供前所未有的幫助,帶來更多的已知條件,這對于解決問題是十分有效的,因此添加和運用輔助線的能力對于學生來說是尤為重要的。
2 輔助線添加原則
首先,在進行有關輔助線的添加過程中,要注意其對隱性條件的挖掘。對于一些幾何題目而言,通過已知條件無法得到直接的結論,這就需要借助于輔助線來完成,通過輔助線能夠讓原有的隱含條件顯現出來,從而找到解決問題的思路。其次,要注意利用輔助線對題目中給出的條件進行整合。當題目所給出的顯性條件較為零散時,就需要利用現有條件進行轉化,通過輔助線的正確添加,讓這些條件在幾何圖形中正確的表達出來,然后將它們當中的對應關系一一找出。再次,在進行輔助線添加的過程中,要注意簡化原則,避免增加難度。當所面臨的圖形呈現出較為復雜狀態時,一般情況下會選擇增加輔助線的方式,將原有復雜的圖形進行劃分,使其成為幾個較為簡單的圖形,這樣能夠有助于原有圖形中隱藏信息的挖掘與提示,借助于這些信息能夠為學生提供一些便捷的解題思路,從而有效地提升學生借助輔助線解決復雜問題的能力。
3 學生添加輔助線能力培養的策略與手段
3.1 三角形中的輔助線
對于幾何圖形為三角形的題目中,常見的輔助線條件有以下三種:(1)對于涉及三角形的題目,中點問題是出現較多的,這時候自然而言就應該聯想到中位線,這樣能夠更好的針對問題進行解決;(2)通過引入角平分線對問題進行解決,利用角平分能夠獲得全等三角形,然后通過借助所構造的三角形給出的條件對問題進行解決。(3)通過給出相等的兩條邊,利用輔助線的添加來獲得全等三角形,然后借助全等三角形的特征對問題進行解決。
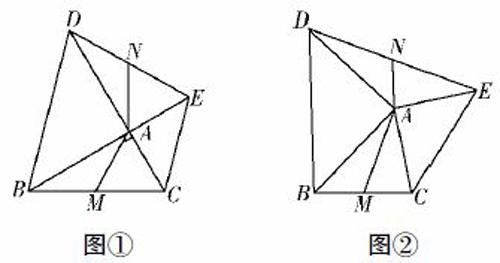
舉個例子,將△ABC的兩條邊AB,AC作為腰,然后借此向外繪制出兩個等腰三角形Rt△ ABD和Rt△ ACE,同時保證∠BAD =∠CAE-90°,將DE聯結起來,則BC,DE的中點分別是M,N。那么其中AM與DE存在怎樣的數量關系以及位置關系。
(1)如上圖①給出,△ABC為直角三角形,那么DE、AM之間存在何種位置關系,線段DE、AM之間又存在何種數量關系?
(2)如果圖①中的等腰Rt △ABD以A為中心逆時針旋轉角度θ(0<θ<90),可以得到圖②,那么上述(1)中得到的兩個結論是否依然成立,并給出其中的理由。
3.2 平行四邊形中的輔助線
對于平行四邊形而言,它擁有自己獨特的特征,如對角相等、對角線相等且對邊之間存在平行關系等。故此,平行四邊形的輔助線添加主要是為了能夠獲得平行亦或是垂直的關系,這樣有助于簡化結題思路,提高結題效率,并有效的鍛煉了學生添加輔助線的能力。
如上圖所示,在四邊形ABCD當中,已知存在AD∥BC,AB∥DC的幾何關系,那么需要證明:AB = DC。
如果學生還沒有進行有關四邊形知識的學習時,首先要將這一題目轉化成三角形進行解答。通過已知的顯性條件可知,AD∥BC,如果將其中的A和C兩個點進行連接就會得到1條輔助線AC,基于平行四邊形內錯角相等的原理,可以得到∠1 =∠2,∠3 =∠4,同時公共邊為AC,基于全等三角形的條件,得到△CDA全等于△ABC,最終證出:AB = DC。
3.3 圓形中的輔助線
(1)通過垂徑定理的運用,在圓心處給出弦的垂線。
(2)利用等圓或者同圓中弦、弧、圓周角、圓心角等之間存在的顯性條件,連接相關圓上的點來進行問題的解決。
(3)直徑作為已知條件出現在題目中時,那么很多情況下需要做出直徑所對的圓周角,利用其為直角的條件來完成題目的解答。
(4)題目中給出切線時,將切點所對應的直徑或半徑連接起來,利用其與切線之間相互垂直的關系。同時在有些題目中需要做出過切點的弦,這樣能夠將其與圓周角、圓心角相互關聯,得到隱性條件。
(5)當題目中給出兩圓相切的條件時,第一可以經過切點做兩圓的公切線,
這樣能夠獲得圓周角與弦切角之間的關系。在有些情況下也會做兩圓的連心線,利用切點在連心線上溝通圓心距與兩圓半徑之間的關系。
上面介紹了不同情形下輔助線的常規添加方法,這些不同情形下也存在著交叉,例如線段的平移、公切線的性質運用、中位線的特征性質等等,在面對問題中,這些輔助線就會成為解決問題最佳的渠道,很多情況下題目的設置者就是為了讓學生通過常規方法無法解決問題,借助于輔助線的“橋梁作用”來進行問題的解決,而輔助線的熟練使用也能夠有效的幫助學生開拓思維,在短時間內獲得解決問題的靈感,從而解決問題,與此同時通過不斷的練習能夠增進學生對于輔助線的認識,提升學生使用輔助線的能力。
基于以上分析,通過輔助線能夠幫助我們更好的解決幾何問題,任課教師在進行教學過程中,應該充分考慮到對學生輔助線運用能力的培養與引導,確保學生能夠充分掌握輔助線運用的技巧,強化學生的理解,讓學生在實際應用中做到游刃有余,從而提升學生解決問題的能力。對于數學教學,任課教師也應該突出幾何方面的內容,讓學生能夠寓教于樂,在獲得興趣的同時更多的掌握實用性知識,并獲得高效解決問題的手段;與此同時通過對學生添加輔助線能力的鍛煉,實現對學生邏輯思維能力以及空間想象能力的培養,同時添加輔助線也是解決問題的“常規武器”,實現化繁為簡,但是在這一過程中也需要注意到學生很容易出現方法掌握效果不佳的情況,因此任課教師在這方面的教學過程中應該尤為注意。
(作者單位:印江土家族苗族自治縣洋溪中學)

